Height of Equilateral Triangle – Formula, Method, Examples

What is the Height of an Equilateral Triangle?

Height is a term that we use to describe how tall an object is when measured vertically. Height of an equilateral triangle is described as the length of the equilateral triangle measured from its top vertex to the base.

Height of Equilateral Triangle: Definition 

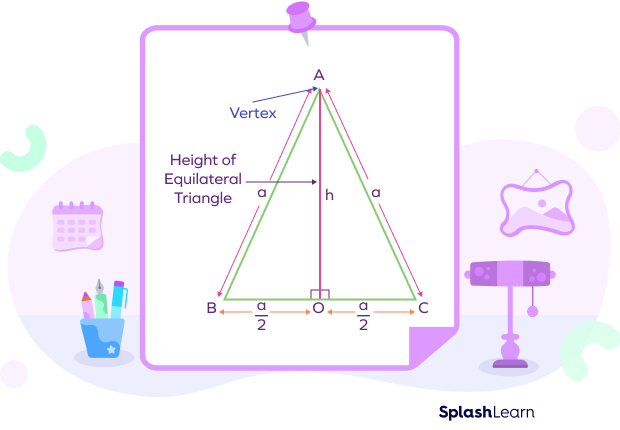
An equilateral triangle has all of its three sides equal in length. In this triangle, one will draw a straight line from one of the vertices to the opposite side of the triangle, and that line divides the equilateral triangle into two parts of equal area, which is termed as the height of an equilateral triangle, please have a look at the attached image where line AO is the height of an equilateral triangle ABC.

What Are the Important Characteristics of Height of Equilateral Triangle?

In the above equilateral triangle ABC, we have defined that AO is the height of the triangle.

• The right-angled triangles formed are $\angle AOB$ and $\angle AOC$. The areas of the two right-angled triangles AOB and AOC formed by AO are equal.

• Interestingly, this line AO, divides $\angle BAC$ into two equal parts, such that,$\angle BAC = \frac{\angle BAO}{2} + \frac{\angle CAO}{2}$ And therefore this line AO is also called as angle bisector of the $\angle BAC$ alongwith the height of an equilateral triangle.

• Further, the line AO divides the opposite side BC into two equal parts of BO and OC, and makes an angle of $90^{\circ}$ with the base BC. So, it is a perpendicular bisector of the line segment BC. 

Height of Equilateral Triangle Formula

The formula for the height of an equilateral triangle (h) is given by

$h = \frac{\sqrt{3}}{2}a$

Here, a represents the side of the equilateral triangle.

Height of Equilateral Triangle Formula Proof

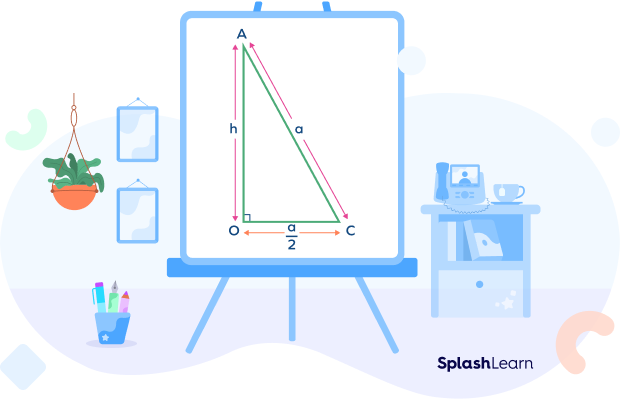
To calculate the height of an equilateral triangle, we will apply the Pythagorean theorem in the right-angled triangle AOC, given below. According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of adjacent and perpendicular. Therefore, in triangle AOC, we can write,

$(AC)^{2} = (AO)^{2} + (OC)^{2}$

$(a)^{2} = (h)^{2} + \bigg(\frac{a}{2} \bigg)^{2}$

$(h)^{2} = (a)^{2} \;-\; \bigg(\frac{a}{2} \bigg)^{2}$

$h^{2} = a^{2}\;-\;\frac{1}{4}a^{2}$

$h^{2} = \frac{3}{4}a^{2}$

$h = \sqrt{\frac{3}{4}a}$

$h = \frac{\sqrt{3}}{2}a$

Therefore, the height of an equilateral triangle formula, h, is $\frac{\sqrt{3}}{2}$ times of the side of the equilateral triangle, a.

How to Find the Height of an Equilateral Triangle When the Side is Given?

If the side of an equilateral triangle is given, then we can simply use the formula to find the height.

$h = \frac{\sqrt{3}}{2}a$ …where ‘a’ is the side

How to Find the Height of an Equilateral Triangle When the Perimeter of the Triangle Is Given?

The perimeter of an object is defined as the measure of the length of the shape. Therefore, for an equilateral triangle the perimeter can be given as the sum of all its three sides, which can be given as,

Perimeter $= a + a + a = 3a$

So, once we know the value of perimeter, we can determine the side of an equilateral triangle by using the formula,

$a = \frac{Perimeter}{3}$

Now, finding the height of an equilateral triangle is easy. We use the formula $h = \frac{\sqrt{3}}{2}a$.

$h = \frac{\sqrt{3}}{2}a = \frac{\sqrt{3}}{2} \times \frac{Perimeter}{3} = \frac{Perimeter}{2\sqrt{3}}$

How to Calculate the Height of an Equilateral Triangle When the Area of the Triangle Is Given?

The area of an equilateral triangle is define with the formula

Area $= \frac{\sqrt{3}}{4}(a)^{2}$

Thus, if we know the value of area of an equilateral triangle then, using the above equation we can determine the value of a, which can be used to estimate the height of an equilateral triangle using the formula,

$h = \frac{\sqrt{3}}{2}a$

Conclusion

In this article, we learned that the height of an equilateral triangle is defined as the distance from the vertex of the triangle and opposite side of this vertex, and this can be calculated mathematically using the derived formulas in the article. All the heights of an equilateral triangle are equal since the sides of the equilateral triangle are equal.

Solved Examples On Height of Equilateral Triangle

1. Find the height of an equilateral triangle if its side is 5 units.

Solution:

Given, side of the equilateral triangle $= a = 5$ units

We have to find the height of the equilateral triangle.

Use the formula to calculate the height of an equilateral triangle.

$h = \frac{\sqrt{3}}{2}a = \frac{\sqrt{3}}{2} \times 5\; units = 4.33$ units

Thus the height of an equilateral triangle is 4.33 units.

2. Find the height of an equilateral triangle if its perimeter is 123 units.

Solution:

Perimeter of the equilateral triangle $= 3a = 12\sqrt{3}$ units

We have to find the height of the equilateral triangle. 

$h = ?$

Therefore, we can use the formula to calculate the height of an equilateral triangle.

$h = \frac{Perimeter}{2\sqrt{3}} = \frac{12\sqrt{3}}{2\sqrt{3}}\; units = 6\; units$

Thus, the height of an equilateral triangle is 3.46 units, which has a perimeter of 12 units.

3. Find the height of an equilateral triangle if its Area is $4\sqrt{3}$ square units.

Solution: Area of the equilateral triangle $= \frac{\sqrt{3}}{4}(a)^{2} = 4\sqrt{3}$ square units

We have to find the height of the equilateral triangle $h = ?$.

Here, first we can use the formula to calculate the side of an equilateral triangle, such that,

$\frac{\sqrt{3}}{4}(a)^{2} = 4\sqrt{3}\; square\; units$

$a^{2} = \frac{4}{\sqrt{3}} \times 4\sqrt{3}\; square\; units$

$a^{2} = 16\; square\; units$

$a = 4\; units$

Now, we can use this value to calculate the height of an equilateral triangle.

$h = \frac{\sqrt{3}}{2}a = \frac{\sqrt{3}}{2} \times 4\; units = 2\sqrt{3}\; units$
Thus, the height of an equilateral triangle is $2\sqrt{3}\;$ units.

Practice Problems On Height of Equilateral Triangle

Frequently Asked Questions On Height of Equilateral Triangle