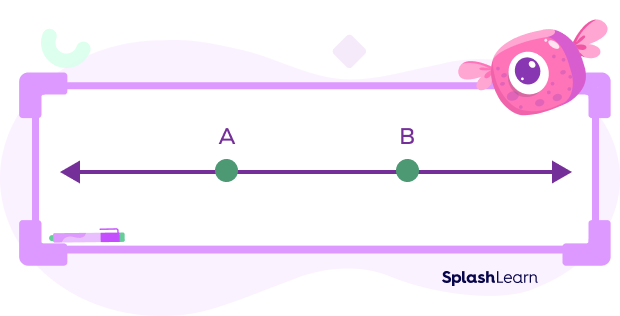
Definition of a Line
A line extends indefinitely in both the directions. Only a portion of a line is drawn and arrow heads are marked at its two ends, indicating that it extends indefinitely in both directions and is denoted by two capital letters. The line has no endpoints.
Recommended Games
Definition of Intersecting Lines in Geometry
Lines are commonly of two types-intersecting and non-intersecting lines. Now you must be wondering what are intersecting and non-intersecting lines? When two lines cross or cut each other they are said to intersect and hence the lines are called intersecting lines.
Let’s understand intersecting lines in detail.
Recommended Worksheets
What are intersecting lines?
When two or more lines cut each other in such a way that there is a common point, it is called an intersecting line.
Two intersecting lines meet once at any point, and it does not matter at what angle they meet.
If the lines are meeting at more than one intersecting point, they cannot be straight lines, and at least one of them is a curve. So the common point is their point of intersection.
An infinite number of lines can be drawn through a given point of intersection.
Let us understand this more elaborately with the help of an example.
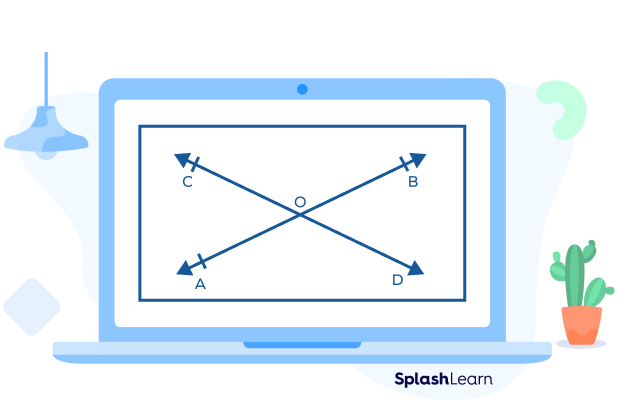
In the below figure, AB and CD are the intersecting lines, and O is the point of intersection.
Properties of Intersecting Lines
These are some of the properties of intersecting lines:
- They always meet at one point and form a pair of vertical angles.
- The intersecting lines meet at one, and only one, point no matter which angle they meet at.
- The intersecting lines form a pair of vertical angles. The opposite angles are equal. Also, the adjacent angles will form a linear pair.
Let us understand more about the vertical angles with the help of an example.
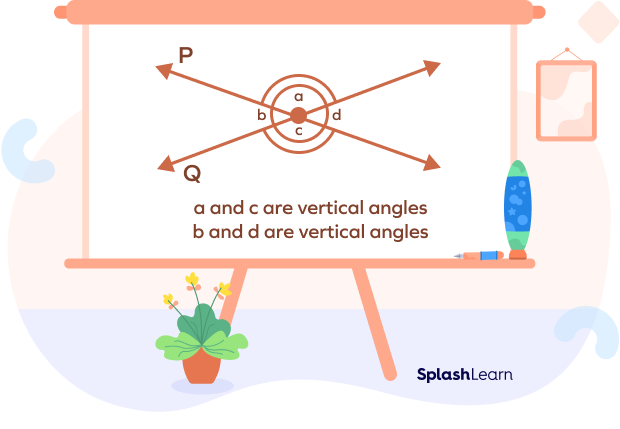
In the above figure, angles made because of the intersection are the vertical angles. Thus, on the line, P and Q, “b and d” and “a and c” are vertical angles meeting at the point of intersection.
The opposite angles are equal.
∠b = ∠d and ∠a = ∠c
Also, the adjacent angles will form a linear pair.
∠a + ∠b = 180°
∠a + ∠d = 180°
∠b + ∠c = 180°
∠c + ∠d = 180°
Examples of Intersecting Lines
We can observe that many examples fit into the category of intersecting lines in our daily lives, such as crossroads, hands of clocks, and scissors.
Fun Facts about Intersecting Lines
- When two lines intersect at more than one given point, those lines will always be curved lines.
- When two lines intersect at a 90-degree angle and create a perpendicular, such lines are known as perpendicular lines.
- All perpendicular lines are intersecting lines but not all intersecting lines are perpendicular lines
Definition of Non-Intersecting Lines in Geometry
It’s not necessary that two lines cross or cut each other. When lines do not intersect or cross each other, the lines are called non-intersecting lines.
Let’s understand non-intersecting lines in detail.
What are Non-intersecting lines?
When two or more lines run concurrently but do not cross each other at any point, they are known as non-intersecting lines. They are also known as parallel lines. II is used as a symbol to denote parallel lines.
Normally, they are at an equal distance, as shown in the figure below:
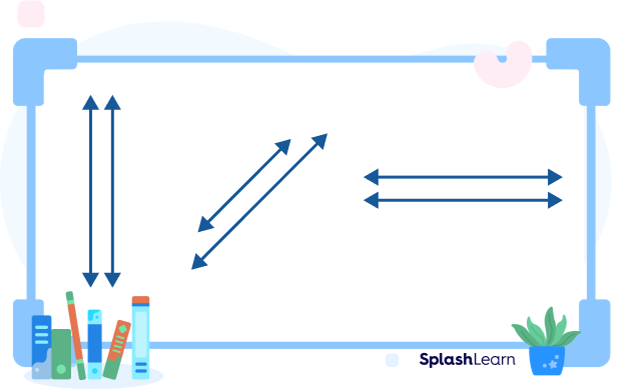
Properties of Non-intersecting Lines
Here are some of the major properties of non-intersecting lines:
- They never meet at any point while running parallelly together.
- Non-intersecting lines have no point of intersection.
- Distance between any two points (one on each line) will always be the same.
- A line can have multiple non-intersecting lines.
Examples of Non-intersecting Lines
In our daily lives, we can observe that many examples fit into the category of non-intersecting lines, such as railway tracks, ladders, and running tracks.

Fun Facts about Non-intersecting Lines
- A line can have multiple lines running parallel to each other.
- Non-intersecting lines can be stretched infinitely, without intersecting each other at any given point.
Let’s practice questions on intersecting and non-intersecting lines
Solved Examples
1. Find whether the lines are intersecting or non-intersecting lines?
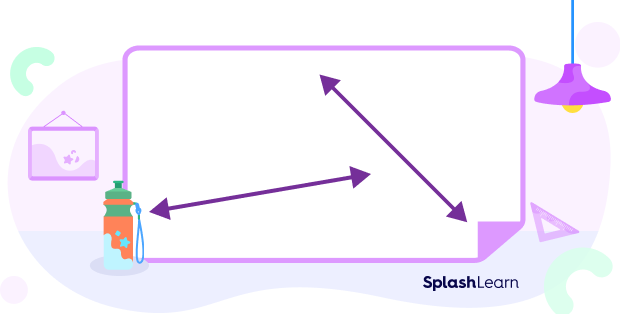
Solution: When the left line is extended to the right-hand side, it will intersect the second line and hence create a pair of intersecting lines.
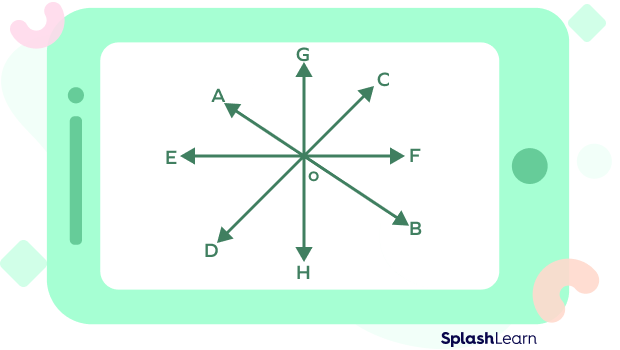
2. Can we create at least four intersecting lines with one common point of intersection?
Solution: Yes, it is possible to have more than one intersecting line with a common point of intersection. The similar thing is explained with the help of an example below.
In this figure, AB, CD, EF, and GH are the four lines that intersect at a common point of intersection O.
3. Classify the pair of lines as intersecting and non-intersecting lines.
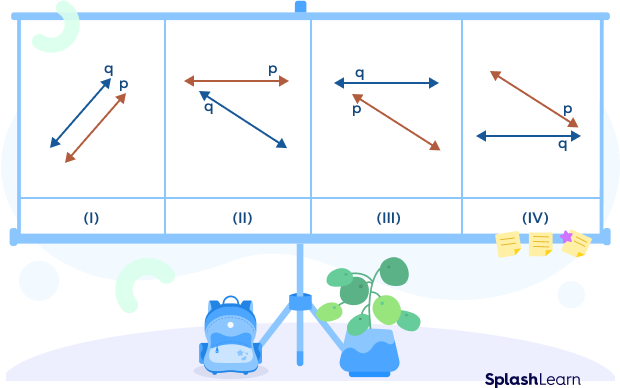
Solution:
Intersecting lines: (II), (III), (IV)
Non-intersecting lines: (i)
4. State whether the given statement is true or false.
a) Adjacent sides of a square are intersecting lines.
b) Intersecting lines have only one point of intersection.
c) Two parallel lines are intersecting lines.
Solution:
- True
- True
- False
Practice Problems
Intersecting and Non-intersecting Lines - Definition with Examples
What is the name of two lines that cross each other.
Intersecting lines cross each other.
With respect to intersecting and non-intersecting lines, pairs of non-intersecting lines will be:
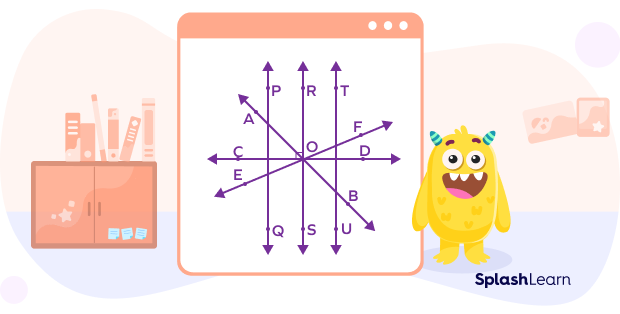
PQ || RS , therefore, they are parallel lines or non-intersecting lines.
Which of these does not represent intersecting lines?
Opposite sides of the rhombus are parallel to each other.
What type of line crosses at the 90° angle?
Perpendicular lines intersect at right angles (90°).
Conclusion
There are commonly two types of lines, intersecting and non-intersecting lines. Intersecting lines meet at a specific point and create equal and opposite angles.
SplashLearn transforms how students learn and study math through a highly engaging and personalized program. Their learning programs are fun and personalized for every child to prepare them for skills required in the twenty-first century.Learn all about the intersecting and non-intersecting lines for grade K-8 on SplashLearn.
Frequently Asked Questions
What is the point of intersection?
When two lines cross each other, the point where they intersect or meet is common to both the lines and is called the point of intersection.
What are vertically opposite angles?
When two lines intersect, they form a pair of vertical angles. The vertical angles that are opposite to each other are called vertically opposite angles.
What are parallel lines?
The lines that do not meet even after extending them are called parallel lines. These lines have no point of intersection.
Define perpendicular angle?
When two lines intersect at exactly 90 degrees, the angle formed because of such an intersection is called a perpendicular angle. Hence, a perpendicular angle always measures 90°.





























