Inverse Relation: Definition, Formula, Graph, Facts, Examples, FAQs

What Is Inverse Relation?

An inverse relation is the inverse of a given relation obtained by Interchanging or swapping the elements of each ordered pair. In other words, if (x, y) is a point in a relation R, then (y, x) is an element in the inverse relation R^–1.

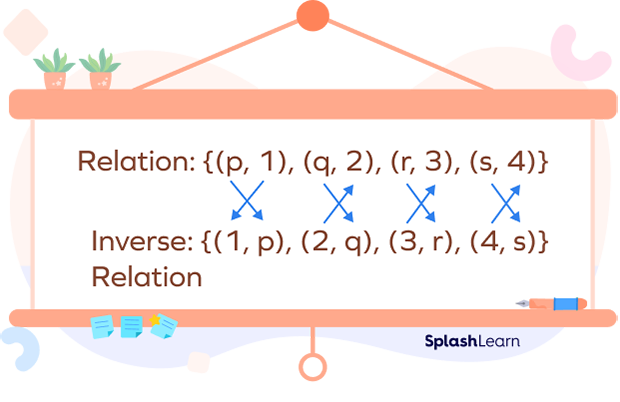
A relation R from set A to B is a subset of the Cartesian product of A and B. R is a subset of A $ \times$ B. The elements of R of the form of an ordered pair (a, b) where a $\in$ A and b $\in$ B.

The inverse relation of R is denoted by R^–1. R^–1 is a subset of B $\times$ A. The elements of R^–1  of the form of an ordered pair (b, a) where b $\in$ B and a$\in$ A.

Inverse Relation: Definition

Inverse relation is defined as the relation obtained by interchanging the elements of each ordered pair in the given relation. By swapping the inverse relation’s domain and range, we can write the inverse relation.

If R is a relation given by $R = \left\{(x,\; y): x ∈ A \text{and} y ∈ B\right\}$. then its inverse is given by 

$R^{-1} = \left\{(y,\; x): y ∈ B \text{and} x ∈ A\right\}$

If R is a relation from set A to set B, then the inverse relationR^–1 is defined from set B to set A. In other words, if $(x,\; y) ∈ R$, then $(y,\; x) ∈ R^{-1}$ and vice versa.

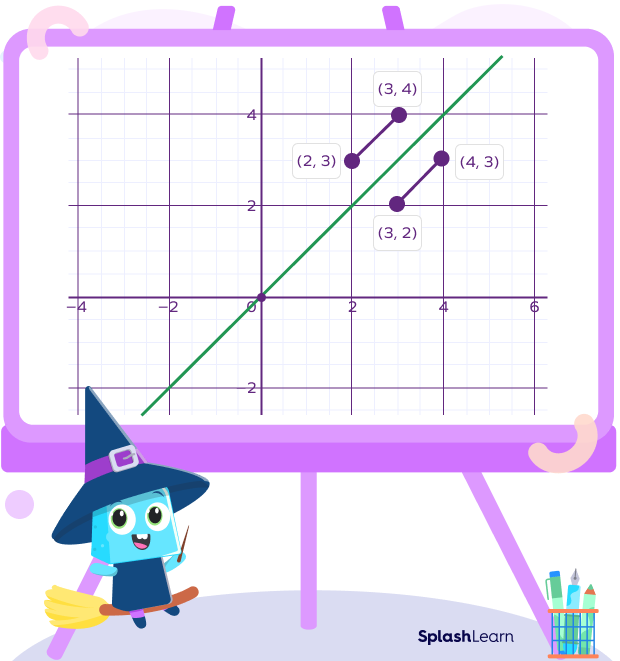
Inverse Relation Graph

If the graph of a relation is given, its inverse can be found by reflecting it along the line $y = x$. To plot the inverse relation graph follow the following steps:

• On the given graph of a relation, select some points.
• To create new points, swap the x and y coordinates of each point.
• Draw a line connecting all of these new points, to get the graph of the inverse relation.

Let’s see an example of elements of a relation and inverse relation on a graph.

Inverse Relation Theorem

Proof: 

Let’s prove the inverse relation statement using the above-mentioned mathematical definition of relation and its inverse.

If (x, y) ∈ R, then (y, x) ∈ R^–1 and vice versa.

Let (x, y) ∈ R ⇔ (y, x) ∈ R^–1

          ⇔ (x, y) ∈ (R^–1)^–1

Every element of R is in (R^–1)^–1.   

Thus, R $\subseteq$ (R^–1)^–1  

Also, following the reverse steps, we get that every element in (R^–1)^–1 is in R.

Thus, (R^–1)^–1 $\subseteq$ R

Hence,  (R^–1)^–1 = R.

Inverse of Algebraic Relation

If an algebraic form of a relation is given, such as R $= \left\{(x,\; y): y = ax + b\right\}$.

Then the steps listed below are used to find its inverse.

Step 1: Interchange or swap the variables x and y.

For the given algebraic equation, after interchanging variables, x = ay + b

Step 2: Now express y in terms of x.

Here, x = ay + b

$\Rightarrow ay = x \;-\; b$

$y = \frac{x \;-\; b}{a}$

Step 3: Then write the given algebraic relation’s inverse as

  R^–1 $= \left\{(x,\; y): y = \frac{x \;-\ b}{a} \right\}$

Note: Check to see if the graphs y = ax + b and $y = \frac{x \;-\; b}{a}$ are symmetric about the line y = x.

Domain and Range of Inverse Relation

The domain and range of a given relation are interchanged when we find the inverse relation.

Domain: 

The set of all first elements of the ordered pairs of R is referred to as the domain of a relation.  The range of R is then the domain of R^–1.

Range: 

The set of all the second element sets is referred to as the range of the relation R. The domain of R is then the range of R^–1.

Example: 

Relation	Inverse
R $= \left\{(2, 4), (4, 16), (6, 36)\right\}$	R–1 $= \left\{(4, 2), (16, 4), (36, 6)\right\}$
Domain of relation R $= \left\{2,4,6\right\}$.	Domain of relation R $= \left\{4,16,36\right\}$.
Range of relation R $= \left\{4,16,36\right\}.$	Range of relation R $= \left\{2,4,6\right\}$

Facts about Inverse Relation

Conclusion

In this article, we have learned the inverse relation definition, their graph, the inverse of algebraic relation, domain, range of inverse relation. Let’s solve a few examples.

Solved Example on Inverse Relation

1. Write the inverse of the relation R = {(1, x), (2, y), (3, z)}.

Solution:

R = {(1, x), (2, y), (3, z)}

The inverse of the relation is obtained by interchanging the elements of each ordered pair in a relation.

Hence, $R^{-1}$ = {(x,1),(y,2),(z,3)}.

2. Find the domain and range of a relation R = { (x, $x^{3}$): x is an odd number less than 10}.

Solution:

R = { (x, $x^{3}$): x is an odd number less than 10}.

Odd numbers less than 10 are 1, 3, 5, 7, 9.

R = {(1, 1³),(3, 3³), (5, 5³), (7, 7³), (9, 9³)}

R = {(1, 1), (3, 27), (5, 125), (7, 343), (9, 729)}

Domain of R = {1, 3, 5, 7, 9}

Range of R = {1, 27, 125, 343, 729}

3. If a relation is given by R = {(x, y); y = 2x + 3,1$\le x \le$ 4}, the domain and range of its inverse relation.

Solution:

R = {(x, y); y = 2x + 3,$1 \le x \le 4$}

For x = 1, y = 5

For x = 2, y = 7

For x = 3, y = 9

For x = 4, y = 11

R = {(1, 5), (2, 7), (3, 9), (4, 11)}

Hence, R^–1 = {(5, 1), (7, 2), (9, 3), (11, 4)}

Domain of R^–1  = {1, 2, 3, 4}

Range of R^–1  = {5, 7, 9, 11}

Practice Problems on Inverse Relation

Frequently Asked Questions on Inverse Relation