What Is the Area of 2D Shapes?
Area of a 2D shape is the quantity that expresses the region enclosed within the boundary of a two-dimensional shape.
2D stands for two-dimensional. 2D shapes are shapes with two dimensions, such as width and height. These shapes do not have thickness or height.
Examples of 2D shapes are square, rectangle, triangle, circle, etc.

How to find the area of 2D shapes? Let’s understand.
Recommended Games
Area of 2D shapes Using Formula
We can also find the area of 2D shapes using formulas. Different shapes have different formulas for calculating the area. Let’s understand how to find the area of a 2D shape using formula. In this section, you can explore the formulas for the area of 2D shapes.
Area of a Square
A square is a 2D shape with four equal sides and all four angles equal to $90^{\circ}$.
The area of a square is the product of its two adjacent sides.
Since all sides of the square are equal.
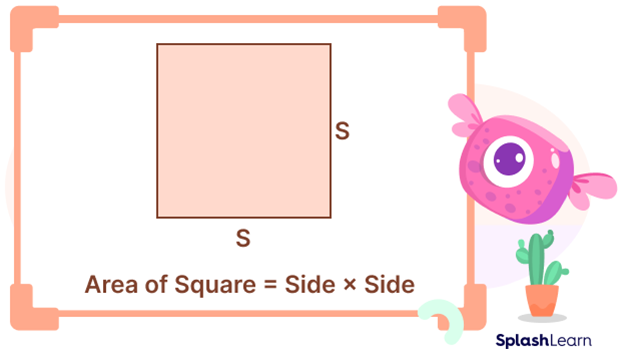
Area of Square $= \text{Side} \times \text{Side}$
Area of Square $= (\text{Side})^{2}$
Area of a Square $ = \text{s}^{2}$
We can see that while measuring the area of a square, we consider only the length of its side.
Let’s take an example of the given square and try to find its area.
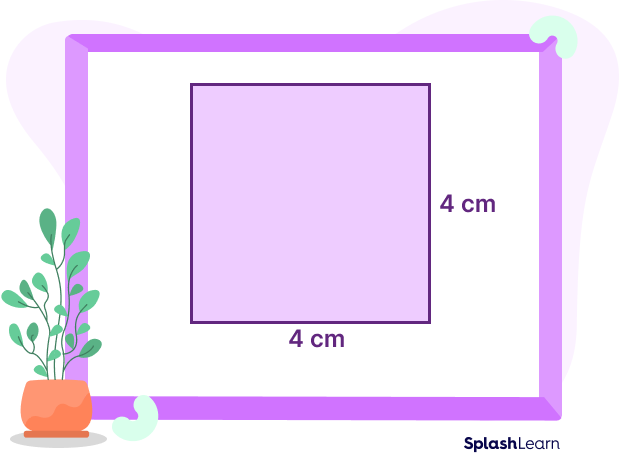
Area of Square $= (\text{Side})^{2}$
Side of the Square $= 4\; \text{cm}$
Area of Square $= (4)^{2} = 16\; \text{cm}^{2}$
Area of a Rectangle
Rectangle is a 2D shape with four sides. Opposite sides of a rectangle are equal and all four angles are equal to $90^{\circ}$.
The area of a rectangle is the product of its two adjacent sides.
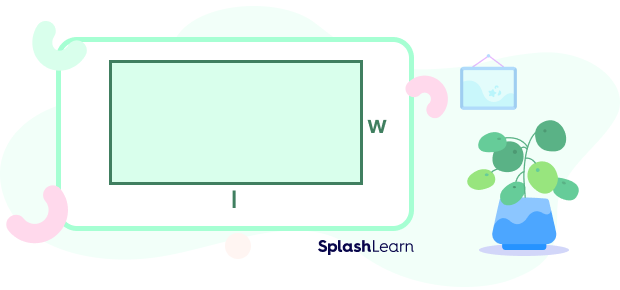
Area of Rectangle $=$ Length $\times$ Width
Area of Rectangle $= \text{l} \times \text{w}$
We can see that while measuring the area of a rectangle, we consider both the length and width of the rectangle.
For example, we have a rectangle here of length 8 cm and width 3 cm. Let’s try to find its area.
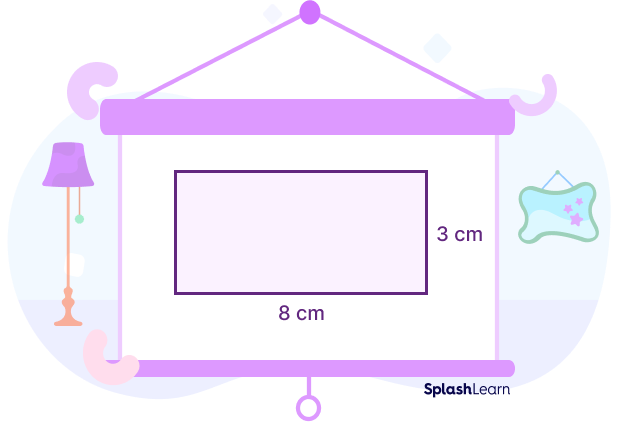
Length of the rectangle, $\text{l} = 8\; \text{cm}$
Width of the rectangle, $\text{w} = 3\; \text{cm}$
Area of the rectangle $= \text{l} \times \text{w}$
Area of the rectangle $= 8 \times 3 = 24\; \text{cm}^{2}$
Area of a Triangle
A triangle is a 2D shape with three sides (edges) and three vertices. A triangle with vertices A, B, and C is denoted as $\Delta$ ABC.
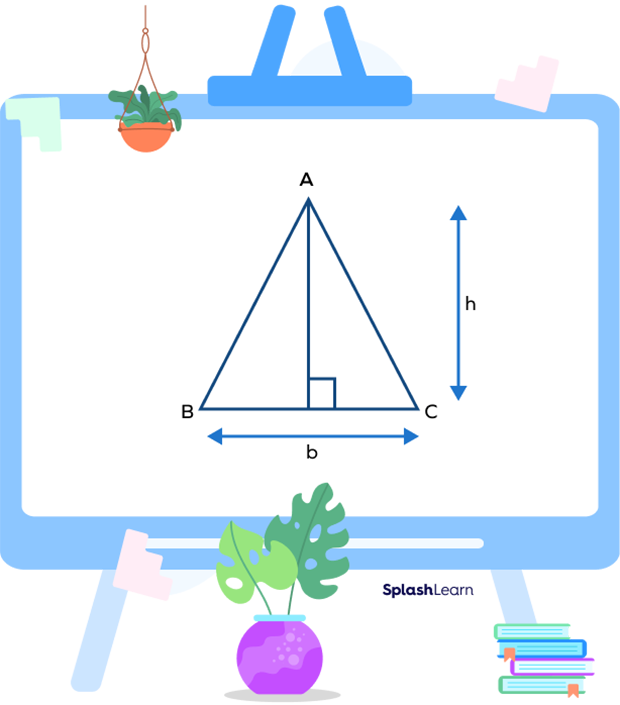
For a given triangle, where the height of the triangle is h and the base is b, the area of the triangle can be calculated by the formula:
Area of triangle $= \frac{1}{2} \times$ base $\times$ height
Area of triangle $= \frac{1}{2} \times \text{b} \times \text{h}$
Note that the base and height of the triangle are perpendicular to each other.
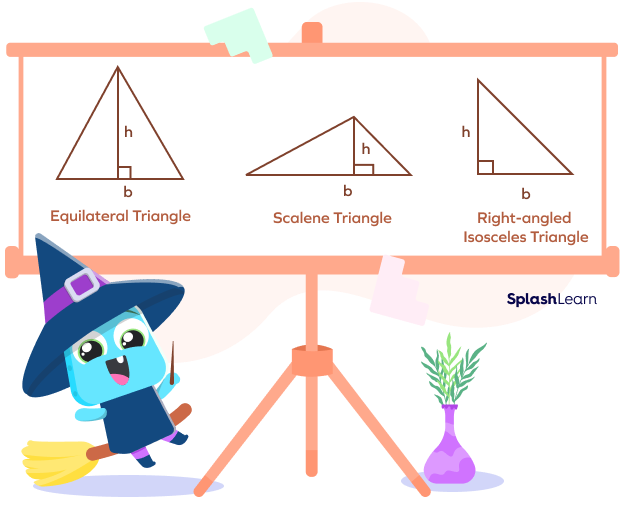
There are different types of triangles, like the equilateral triangle, isosceles triangle, and right-angled triangle, but the formula for the area of all kinds of triangles is the same.
The following image shows base and height for an equilateral triangle, scalene triangle, and right-angled isosceles triangle. Note that the base equals height in a right angled isosceles triangle.
Let’s take an example of the given triangle ABC.
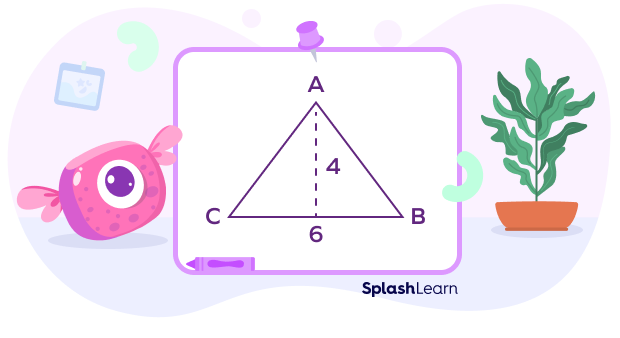
In the triangle ABC, the base measures 6 units and the height measures 4 units.
Area of triangle $= \frac{1}{2} \times$ base $\times$ height
Area of triangle ABC $= \frac{1}{2} \times \text{b} \times \text{h}$
$= \frac{1}{2} \times 6 \times 4$
$= 12$ sq. units
Recommended Worksheets
Area of 2D Figures by Counting Squares
Look at the shapes given below. We won’t be able to use basic formulas to find out the area of such irregular 2D shapes. In order to calculate the area of two dimensional shapes where we cannot apply any formula, we have another method, which is by counting squares on the grid.

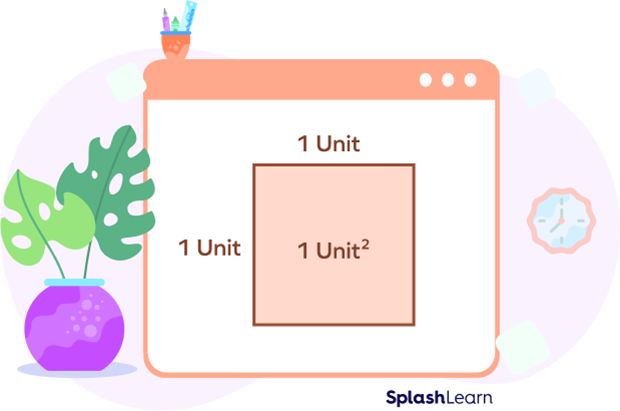
Now, we know that area is the region inside the boundary of the 2D shape, we can express the area in terms of unit squares. A square whose side is of length 1 unit has an area of 1 square unit.
To find the area of 2D figures using this method, we count the number of squares that cover the surface of the figure.
While counting the squares, we follow these rules:
- If the figure is covered by less than half a square, count it as zero.
- If the figure is covered by more than half a square, count it as 1 unit.
- If the figure is covered by exactly half a square, count it as $\frac{1}{2}$ a unit.
- If the figure is covered by a full square, count it as 1 unit.
Let us find the area of the given pentagon.

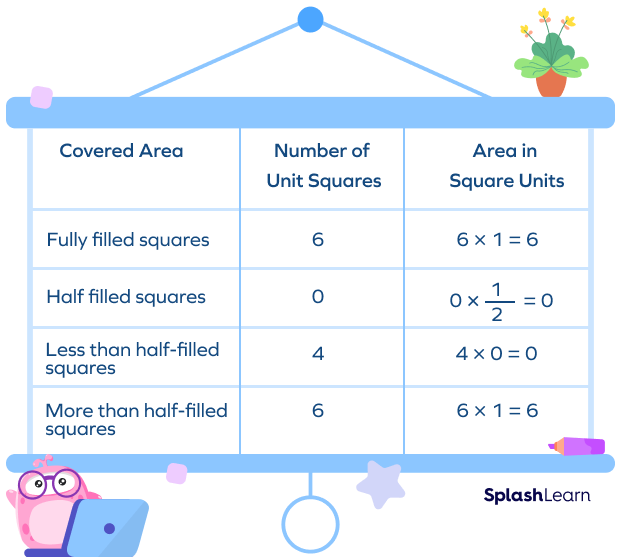
Area of the pentagon is the total area of all the squares covered $= 6 + 0 + 0 + 6 = 12$ square units
Area of irregular figures can be easily found using this method.
Fun Facts!
- Among all the shapes with the same perimeter, a circle has the largest area.
- A rectangle with all sides equal is called a square.
- All squares are rectangles but all rectangles are not squares.
- Note that the term surface area is used to represent the total area of all the outer faces of a 3D solid figure. Area is the region bounded within the boundaries of a 2D shape. Thus, the surface area of 2D shapes is nothing but the area of a 2D shape.
Conclusion
The next time you want to roll out a grass lawn to cover your front yard, you can find the area of the yard to figure out the size of roll-out lawn needed to make your front yard beautiful.
Solved Examples on Area of 2D Shapes
- Find the area of the given shape.
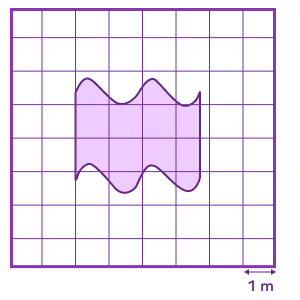
Solution: Let’s count the number of unit squares (completely filled, half-filled, more than half-filled, less than half-filled). Completely filled unit squares are marked in the image below for reference.
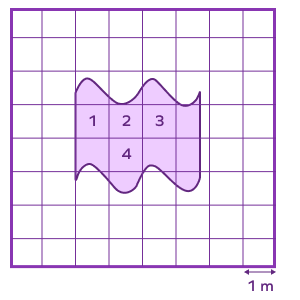
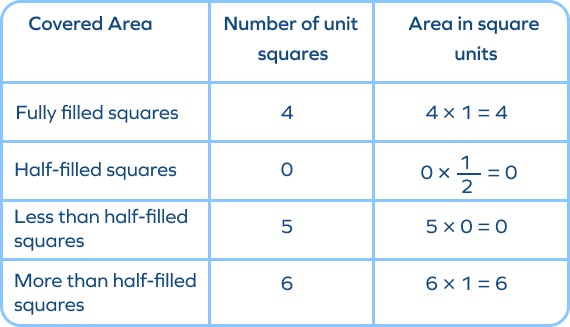
Area of the irregular 2D shape is the total area of all the squares covered $= 4 + 0 + 0 + 6 = 10\; \text{m}^{2}$
2. Find the length of the rectangle whose area is $35\; \text{m}^{2}$ and width is 5 m.
Solution:
Area $= 35\; \text{m}^{2}$
Width $= 5\; \text{m}$
Area of Rectangle $= \text{l} \times \text{w}$
$35 = \text{l} \times 5$
$355 = \text{l}$
$\text{l} = 7\; \text{m}$
Length of the rectangle is 7 m.
3. The floor of a rectangular hall is to be covered with a carpet 200 cm wide. If the length and width of the hall are 20 m and 18 m respectively, find the cost of the carpet at the rate of $2 per meter.
Solution:
Area of the hall $= 20 \times 18 = 360\; \text{m}^{2}$
Width of the carpet $= 200\; \text{cm} = 200 \div 100 = 2\; \text{m}$
Area of carpet $=$ Area of hall
Therefore, length of the carpet $= \frac{Area of the hall}{Width of the carpet} = \frac{360}{2} = 180\; \text{m}$
Rate of the carpet $= \$2$ per meter
Therefore, cost of the carpet $= \$ (180 \times 2) = \$ 360$
4. Find the area of the given figure.
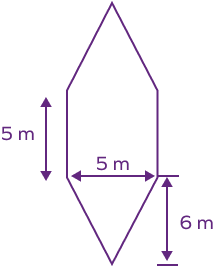
Solution:
The given figure can be divided into a square and triangles as shown.
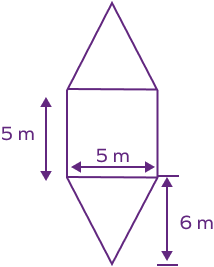
Area of the figure $=$ Area of triangle $1 +$ Area of triangle $2 +$ Area of the square
Area of the triangle $1 =$ Area of the triangle $2 = \frac{1}{2} \times$ base $\times$ height
$= \frac{1}{2} \times 5 \times 6$
$= 15\; \text{m}^{2}$
Area of Square $= (\text{Side})^{2}$
$= 5^{2} = 25\; \text{m}^{2}$
Area of the figure $= 15 + 15 + 25 = 55\; \text{m}^{2}$
Practice Problems on Area of 2D Shapes
Area of 2D Shapes – Definition, Formulas & Examples
Find the area of the hexagon.
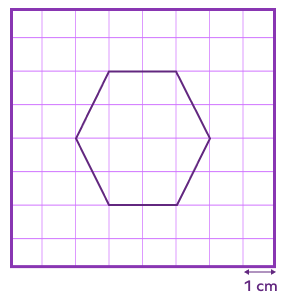
Count the number of squares enclosed by the hexagon.
Complete squares $= 8$
$\gt \frac{1}{2}$ square $= 4$
$\lt \frac{1}{2}$ square $= 4$
Area $= (8 \times 1) + (4 \times 1) + (4 \times 0) = 8 + 4 + 0 = 12\; \text{cm}^{2}$
Find the area of a square whose side is 7 cm.
Area of Square $=$ Side $\times$ Side $= 7 \times 7 = 49\; \text{cm}^{2}$
A marble tile measures 30 cm by 20 cm. How many tiles will be required to cover a wall of size 6 m by 2 m?
Area of wall $= 6 \times 2 = 12\; \text{m}^{2}$
$= 12,000\; \text{cm}^{2} ( 1\; \text{m}^{2} = 10000\; \text{cm}^{2})$
Area of one tile $= 30 \times 20 = 600\; \text{cm}^{2}$
Therefore, number of tiles $= \frac{Area of the wall}{Area of the tile} = \frac{12000}{600} = 200$
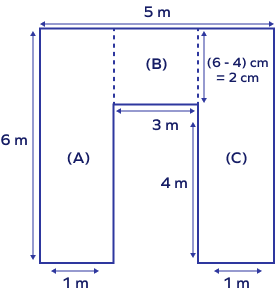
Find the area of the given figure.
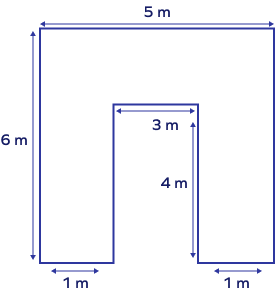
Split the figure into rectangles as shown.
Area of the figure $=$ Area of rectangle A $+$ Area of rectangle B $+$ Area of rectangle C
Area of rectangle $\text{A} = 6 \times 1 = 6\; \text{m}^{2}$
Area of rectangle $\text{B} = 3 \times 2 = 6\; \text{m}^{2}$
Area of rectangle $\text{C} = 6 \times 1 = 6\; \text{m}^{2}$
Area of figure $= 6 + 6 + 6 = 18\; \text{m}^{2}$
Frequently Asked Questions on Area of 2D Shapes
What are polygons?
2D shapes that are made up of straight lines and form a simple closed figure are called polygons.
For example, square, rectangle, and triangle are examples of polygons.

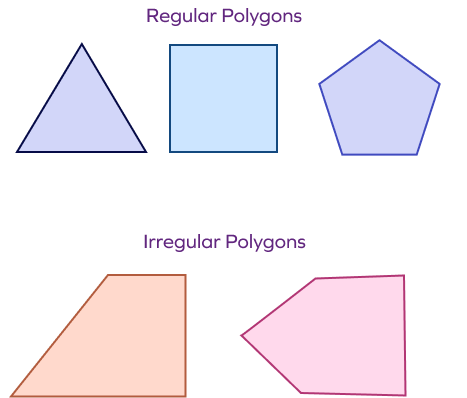
What are regular and irregular polygons?
Regular polygons are polygons with equal sides and angles. Example: equilateral triangle, square, regular pentagon, etc. Irregular polygons are polygons with irregular shapes. Their sides and angles are not equal.
Give a real-life application of the area.
Covering a table with a sheet is a real-life application of area of 2D shapes. The whole surface of the table is to be covered with a sheet, so by finding the area of the surface of the table, we can find out the size of the sheet required to cover the surface of the table.




































