What is Area of a Quadrilateral?
A quadrilateral is a polygon we obtain by joining four vertices, and it has four sides and four angles. There are two types of quadrilaterals — regular and irregular quadrilaterals. Some examples of the quadrilaterals are square, rectangle, rhombus, trapezium, and parallelogram.The area of a polygon refers to the space occupied by the flat shape. It is the combined sum of the area of the regular and irregular triangles within.
Measuring the area of a quadrilateral
To evaluate the area of a quadrilateral, we divide it into two basic geometric figures, such as triangles. Then we find the area of the two individual triangles using the formula and add these areas to find the area of the quadrilateral.
Calculating the area of a quadrilateral
- Draw a diagonal AC connecting two opposite vertices of the quadrilateral ABCD.
- Draw a perpendicular each from the other two vertices
(B and D) on the diagonal AC.
- The area of the quadrilateral will be:
Area of quadrilateral ABCD = Area of △ABC + Area of △ADC
So, area of quadrilateral ABCD = (½ × AC × BE) + (½ × AC × DF)
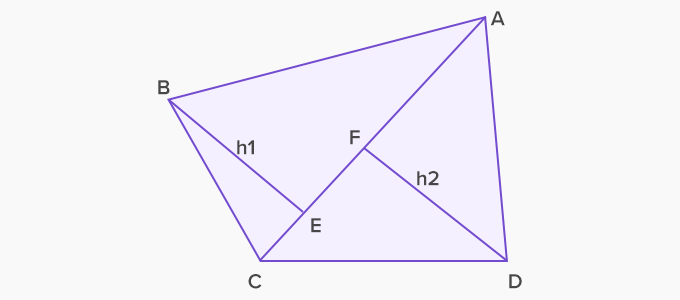
We can calculate the area of different types of quadrilaterals by using the given formula. For the quadrilateral ABCD, if we use centimeter as the unit of measurement, the unit of measure for the area will be cm2 .
Recommended Games
Area of a Parallelogram
To evaluate the area of a parallelogram, draw a perpendicular from one of the vertices to the base. This perpendicular is the height. Thus, the area will be the product of base and height.
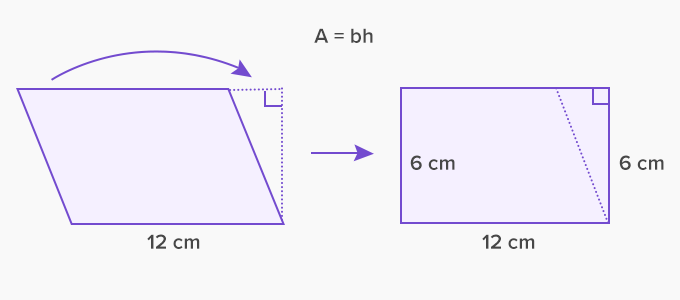
Area of parallelogram = base x heightArea = 12 × 6 = 72 cm
Recommended Worksheets
Area of a Rhombus
To find the area of a rhombus, we divide the quadrilateral into two equal isosceles triangles using the two diagonals. In the given rhombus ABCD, the point of intersection of these diagonals is E. Thus the area of the rhombus is:
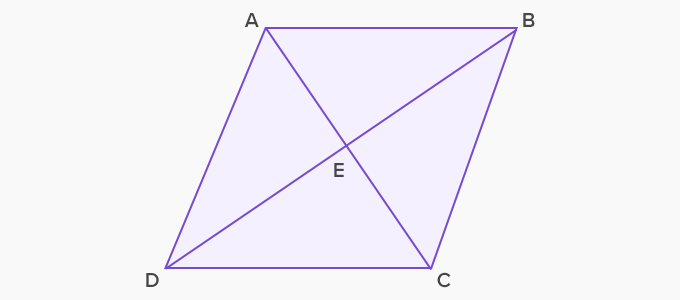
Area of rhombus ABCD = Area of △ABC + Area of △ADC
⟹ Area of rhombus ABCD = (½ x AC x BE) + (½ x AC x ED)
⟹ Area of rhombus ABCD = ½ x AC (BE + ED)
⟹ Area of rhombus ABCD = ½ x AC x BD
Area of a Square
Using this relationship we can also find the area of a square ABCD
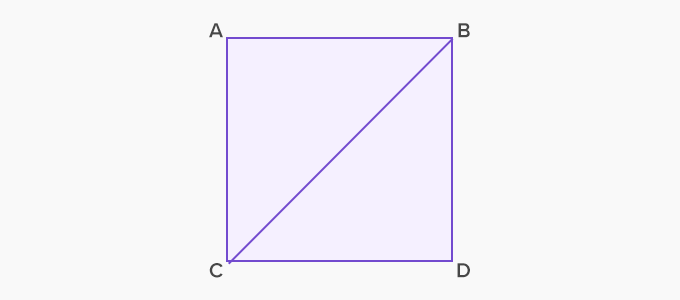
Area of square ABCD = Area of △ABC + Area of △BCD
⟹ Area of △ABC = ½ * AC * AB
⟹ Area of △ABC = ½ * AC * AC (as AC = AB)
⟹ Area of △ABC = ½ * AC2
Similarly, Area of △BCD = ½ * CD2
Since, AC = CD, Area of △BCD will be ½ * AC2
Thus, area of square ABCD = 2 * (½ * AC2) = AC2
Hence, Area of square ABCD is the square of the side.
Area of a Rectangle
The area of a rectangle using the above formula will yield the product of its two adjacent sides, base and height. We represent it as:
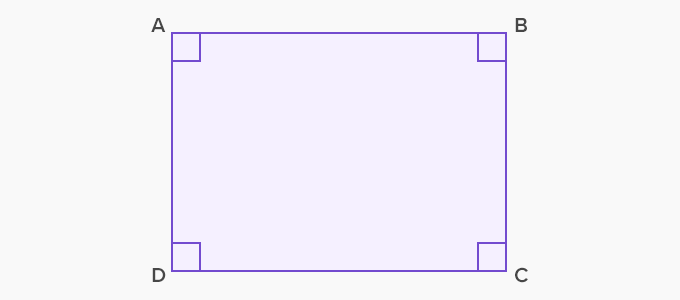
- Area (ABCD) = AB x BC
Application
The real-life application of quadrilaterals and its area are highly useful in the fields of design, agriculture, and architecture. The concept is highly useful in the advanced designing of navigation maps scaled to actual distances and areas with precision.
The area covered by a quadrilateral formed by joining four different places on a map
Fun Facts
- The term quadrilateral is a combination of words Quadri + Lateral which means “four sides”.
- Except for squares, all the quadrilaterals are irregular quadrilaterals. They are also known as “Quadrangle” and “Tetragon” (four and a polygon).
- The sum of all the angles within a quadrilateral is always 360°.
Related Math Vocabulary
Practice Problems
Area of a Quadrilateral
The area of a parallelogram with a base of 5 units is 30 square units. What is the height of the parallelogram?
The area of a parallelogram is base ✕ height.
So, the height of the parallelogram = area/base,
i.e., 30 square units/5 units or 6 units.
The area of a rhombus with a diagonal of length 8 cm is 24 square cm. What is the length of the other diagonal?
The area of a rhombus is 1/2 ✕ product of diagonals.
So, the length of other diagonal = (2 ✕ area)/first diagonal,
i.e., (2 ✕ 24 square cm)/8 cm = 6 cm.
What is the area of a parallelogram with a base of 7 cm and a height of 8 cm?
The area of a parallelogram is base ✕ height,
i.e., 7 cm ✕ 8 cm or 56 square cm.
What is the area of a rhombus with diagonals 6 units and 9 units?
The area of a rhombus is 1/2 ✕ product of diagonals,
i.e., 1/2 ✕ 6 units ✕ 9 units or 27 square units.
Frequently Asked Questions
How to find the area of a quadrilateral?
To find the area of a quadrilateral, divide it into two triangles using a diagonal. Then calculate the area of each triangle and add them up.
What is the formula to find the area of a quadrilateral?
Area of the Quadrilateral = (1/2) × d × (h1 + h2). Here, d = diagonal of the quadrilateral, h1, h2 = heights of the triangles created on either side of the diagonal (d)
What is the unit of the area of a quadrilateral?
The unit of area of a quadrilateral is the same as other shapes, that is, square units of length (square meter, square inches, etc.)
What is the formula to find the area of special quadrilaterals?
These are the formulas to find the area of special quadrilaterals: – Area of a Square = side × side – Area of a Rectangle = length × width – Area of a Parallelogram = base × height – Area of a Trapezoid = 1/2 × (base1 + base2) × height – Area of a Rhombus = 1/2 × diagonal1 × diagonal2 – Area of a Kite = 1/2 × diagonal1 × diagonal2




































