Can you draw a tree that is 87.6 feet tall on a piece of paper?
Obviously not. We would need a jumbo-sized piece of paper, and that still won’t help us. So, what would be the easiest way to draw a tree on a piece of paper? Scaling, of course!
What is Scaling in Math?
You must be wondering what does scaling mean in Math? Scaling is a procedure through which we draw an object that is proportional to the actual size of the object. Scaling in geometry means that we are either enlarging or shrinking figures so that they retain their basic shape. When we scale figures, they are known as similar figures.
In the above example of scaling, the two rectangles are similar because their basic shapes are the same even if one is smaller and the other is larger. In order to scale images, we need a scale.
Recommended Games
What is a Scale Factor
Scale is the ratio to represent the relation between the dimensions of a model or scaled figure and the corresponding dimensions of the actual figure or an object. Scale factor, on the other hand, is a number by which all the components of an object are multiplied in order to create an enlarged or reduced figure. Scale and scale factor are mostly used in blueprints that are used for the construction of buildings.
To draw real-world objects on a piece of paper, we need a scale to describe our measurements accurately. For example, a scale of 1:10 means that the size of 1 unit in the drawing would represent 10 units in the real world. For example, if a lion is of height 50 inches in the real world and is represented as 5 inches on the drawing, it shows that a scale of 1:10 has been used.

The scale factor can be calculated if the dimensions of the original figure and the dimensions of the increased or decreased figures are known.
Scale = Dimensions of the new shape : Dimensions of the original shape
Scale Factor = Dimensions of the new shape Dimensions of the original shape
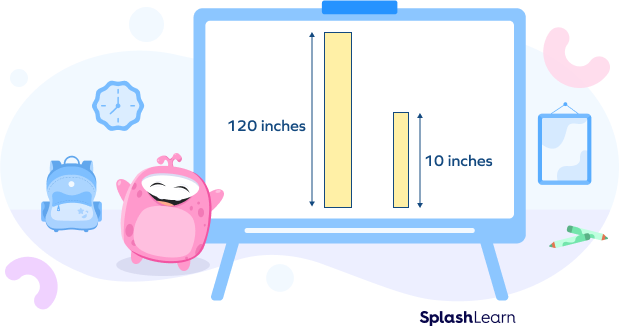
For example, if a wall is supposed to be constructed to 120 inches high in the real world and represented as 10 inches in the blueprint, the scale will be 10:120 or 1:12, whereas the scale factor will be $\frac{1}{12}$.
Recommended Worksheets
Types of Scaling
1. Scale up
We scale up when we want to enlarge a smaller figure to a bigger one. In other words, when the size of the figure is increased, it means it has scaled up. When we scale up, the scale factor can be calculated using the following formula:
Scale Factor = Dimensions of the new shape Dimensions of the original shape
Scale up factor = Larger figure dimensions ÷ Smaller figure dimensions
We prefer to scale up when the object is very small. For example, we have to draw a butterfly on a piece of paper in order to study its parts. Since the butterfly is small in size, we would prefer to scale it up, as shown below.
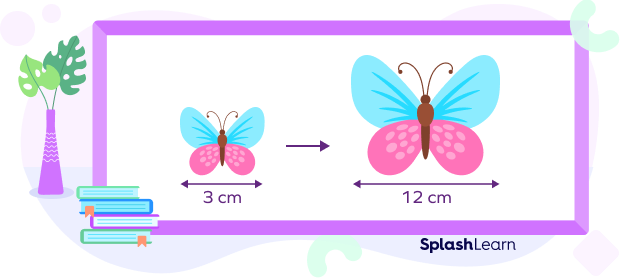
Scale factor = $\frac{12}{3}=4\gt1$
As shown in the above example, the scale factor to scale up is always greater than 1. Let us look at one more example: If the dimension of the larger figure is 18 and that of the smaller one is 6, we get the scale factor: 18 ÷ 6 = 3, which is also greater than 1. Here, the smaller figure is called preimage and the enlarged figure is called image.
2. Scale down
We scale down when we want to reduce a bigger figure to a smaller one. In this case, the scale factor can be calculated using the following formula:
Scale Factor = Dimensions of the new shape Dimensions of the original shape
Scale down factor = Smaller figure dimensions ÷ Larger figure dimensions
For example, we have to construct a bedroom of size 180 inches by 168 inches. We need to draw its blueprint first to set up the furniture, like bed, nightstands, etc. So, we will scale down the bedroom to 15 inches by 14 inches.
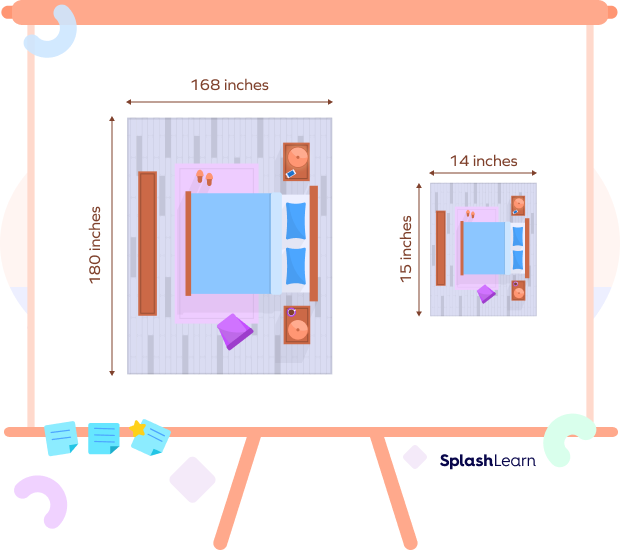
Scale factor = $\frac{15}{180}=\frac{1}{12}\lt1$
As shown in the above example, the scale factor to scale down is always less than 1. Let us take one more example: If the dimension of the smaller figure is 6 and that of the larger one is 24, let us place this in the formula, which makes it: 6 ÷ 24 = 1/4. Here, the larger figure is called preimage and the contracted figure is called image.
Solved Examples
Example 1. There are two similar pentagons given below. Find the scale factor.
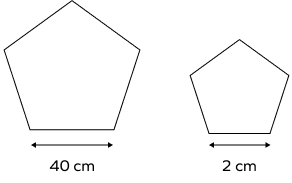
Solution: Scale Factor = $\frac{2}{40}=\frac{1}{20}$
Example 2. What will be the height of the actual object if the height of the contracted figure is 4 units and the scale is 1:25?
Solution: $\frac{Scaled height}{Actual height}=\frac{1}{25}$
$\frac{4}{Actual height}=\frac{1}{25}$
Actual height = $4\times25$ = 100 units
Example 3. What is the scale formula if an image has to be enlarged?
Solution: If we have to enlarge or scale up an image, the scale factor, which is denoted by k, is more than 1, i.e., k > 1.
Scale Factor = Dimensions of the new shape Dimensions of the original shape
The scale factor formula = Larger figure dimensions ÷ Smaller figure dimensions
Practice Problems
Scaling in Math – Definition with Examples
What will be the scale factor if the smaller rectangle is resized to the bigger rectangle with the given dimensions?
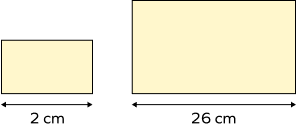
Scale factor = $\frac{26}{2}$ = 13
If k = 1, which of the following is true?
Since k = 1, actual size = scaled size.
A cube of dimensions 8 units by 12 units by 16 units was decreased by a scale factor of 1/4 . Find the new dimensions of the cube.
The new dimensions will be:$8\times\frac{1}{4};12\times\frac{1}{4};16\times\frac{1}{4}$ = 2 units by 3 units by 4 units
Frequently Asked Questions
What is the difference between scale and scale factor?
Scale is the ratio that defines the relation between the actual figure and its model. It is used in maps to represent the actual figures in smaller units. For example, a scale of 1:5 means 1 on the map represents the size of 5 in the real world.
Scale factor, on the other hand, is a number that is used to increase or decrease the size of a figure. For example, if a triangle needs to be increased in size using a scale factor of 3, and the sides of the triangle are a, b, and c, then the new sides of the triangle will be 3a, 3b, and 3c.
What happens if the scale factor is less than 1?
If the scale factor is less than 1 (k <1), then the new figure will have smaller dimensions as compared to the original figure.
When do we use scaling?
Scaling is used when the size of any geometrical figure or shape or an object can be changed with respect to its original size. When things are too large, we use scale factors to calculate smaller measurements. When things are too small, we use scale factors to calculate bigger measurements.





















