What Is the Median of a Triangle?
Triangle is a closed figure with three sides, three interior angles, and three vertices. A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to that vertex.
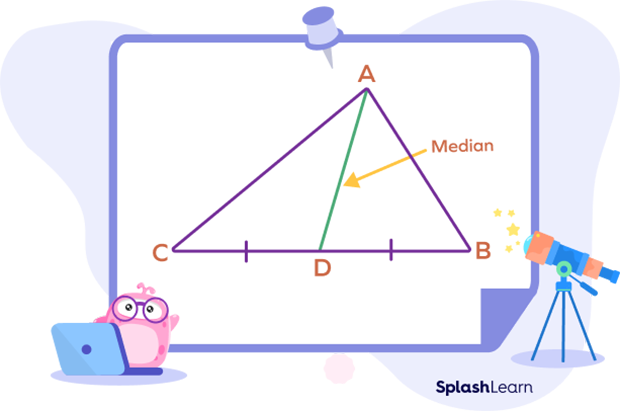
In the above figure, A, B, and C are vertices of the triangle.
D is the midpoint of the line segment BC.
The line AB is a median of the triangle ABC.
Recommended Games
Definition of Median of a Triangle
A median of a triangle can be defined as a line segment drawn from a vertex of a triangle that bisects the opposite side of a triangle.
Recommended Worksheets
Properties of Median of Triangle
Let’s discuss some important properties of the median of triangles.
- It bisects the opposite side into two equal parts.
- Every triangle has three medians, one from each vertex to its opposite side.
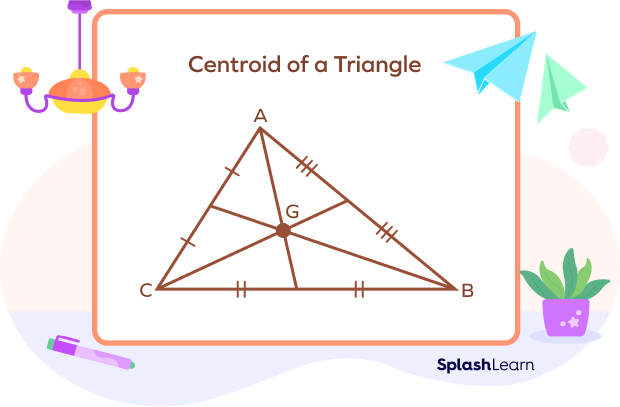
- No matter what the shape of the triangle is, the three medians always meet at a single point.
- The points where the three medians meet are called the centroid of the triangle.
- The median of a triangle divides the triangle into two triangles having equal area.
- The three medians of a triangle divide the triangle into six smaller triangles of equal area.
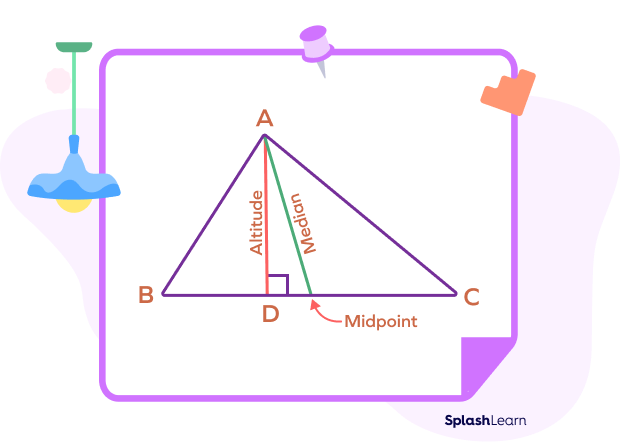
Difference between Altitude and Median of a Triangle
In any triangle, the median and altitude are not the same. An altitude of a triangle is a line segment that starts from the vertex and meets the opposite side at a right angle. It is the shortest distance between the vertex and the line opposite to that vertex. Whereas, a median is a line segment that connects a vertex to the midpoint point of the opposite side.
How to Find the Median of a Triangle
The length of the median of a triangle can be determined using the basic formula, which can be derived from Apollonius’s Theorem.
Apollonius’s Theorem to Find Median of a Triangle
It states that in any triangle, the sum of the squares on any two sides is equal to twice the square on half the third side together with twice the square on the median that bisects the third side.
The above-mentioned theorem is a bit wordy but can be transformed into a formula that gives the median of the triangle formula.
Median of Triangle Formula
Let us consider a, b, and c are the lengths of the sides of a triangle, and $\text{m}_{a},\; \text{m}_{b},$ and $m_{c}$ are the medians formed on side a, side b, and side c respectively.
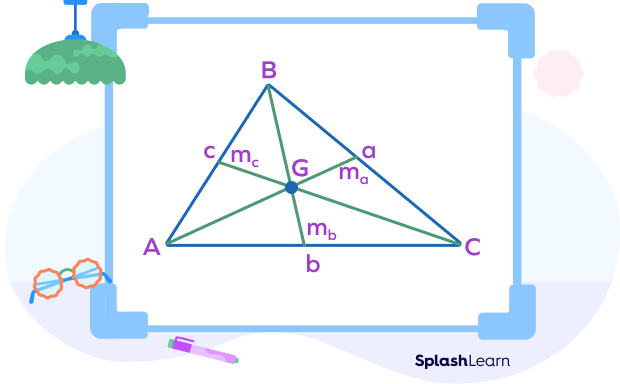
The first median of a triangle $(m_{a})$ drawn on the side “a” can be calculated using the formula,
$m^{a}=\sqrt{\frac{2b^2 +2c^2\;-\;a^2}{4}}$
Similarly, the second median of a triangle $(m_{b})$ drawn on the side “b” can be calculated using the formula,
$m_{b} = \sqrt{\frac{2a^2 +2c^2\;-\;b^2}{4}}$
Similarly, the third median of a triangle $(m_{c})$ drawn on the side “c” can be calculated using the formula,
$m_{c} = \sqrt{\frac{2a^2 +2b^2\;-\;c^2}{4}}$
How to find the Median of the Triangle Using Coordinates of Vertices
When we have the coordinates of the three vertices of a triangle, we can find out the length of the median of the triangle by following the steps given below.
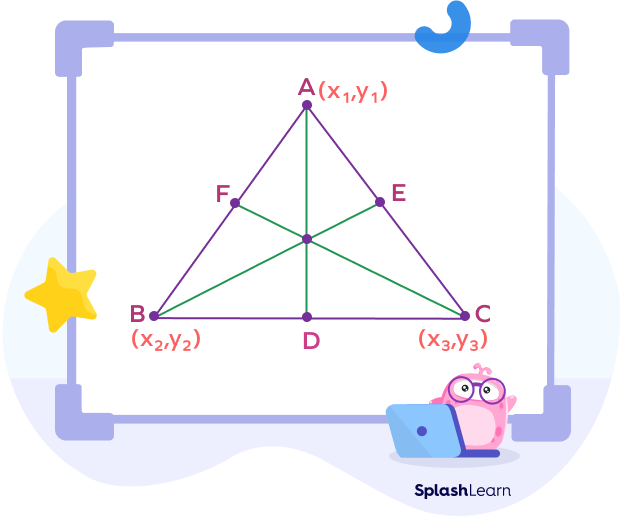
Step 1:
Using the midpoint formula, find the midpoint of BC, which points D. Let the coordinates of point D be $(a_{1},\; b_{1})$.
In geometry, the midpoint is the middle point of a line segment. For any two points $(x_{1},\; y_{1})$ and $(x_{2}, y_{2})$ midpoint is given by $\bigg(\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2}\bigg)$
Here for point D, the midpoint is calculated as,
D$(a_{1},\;b_{1}) = \bigg(\frac{x_{2} + x_{3}}{2},\; \frac{y_{2} + y_{3}}{2}\bigg)$
Step 2:
Find the length of median AD using the distance formula.
In geometry, the distance formula is used to find the length or distance between two points when their coordinates are given. For any two points $(x_{1},\; y_{1})$ and $(x_{2},\; y_{2})$ distance formula is given by $\sqrt{(x_{2}\;-\;x_{1})^{2} + (y_{2}\;-\;y_{1})^{2}}$
Here, the length of median AD $ = \sqrt{(a_{1}\;-\;x_{1})2 + (b_{1}\;-\;y_{1})^{2}}$
Similarly, we can find the lengths of median BE and CF.
Fun Facts!
- The points where the medians of a triangle meet are known as the centroid. It is also called the center of gravity of the triangle.
- The median of a triangle divides the triangle into two triangles having equal area.
- The three medians of a triangle divide the triangle into six smaller triangles of equal area.
- The sum of the length of three medians of a triangle is greater than its perimeter.
- The medians of congruent triangles are equal because the corresponding parts of congruent triangles are congruent.
- In a scalene triangle, the medians have different lengths.
- In an equilateral triangle, the length of the medians is the same.
- The altitude of a triangle may lie inside or outside the triangle
- The centroid of a triangle divides each median in the ratio 2:1.
Conclusion
In this article, we learned about the median and altitude of a triangle, properties of the median of a triangle, and different methods to find the median of a triangle.
Solved Examples On Median of a Triangle
- In the figure given below identify the medians of the triangle. What is their point of intersection called?
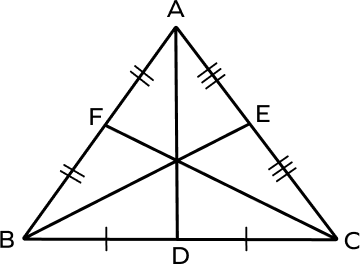
Solution:
Medians of triangle ABC are AD, BE, and CF. They bisect the opposite sides.
The points of intersection of medians AD, BE, and CF is known as centroid and it is usually represented by G.
- For the given triangle PQR, G is the centroid and QR $= 12$ inches. Find the length of TR.
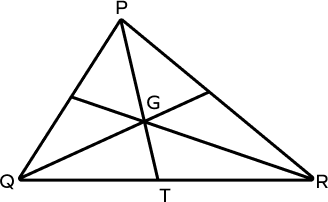
Solution:
For the given triangle PQR, PT is the median of the triangle which divides the side QR into two equal parts.
Since QR $= 12$ inches (given)
Thus, TR $= \frac{12}{2} = 6$ inches.
- In the given figure, AD is a median, if the area of the triangle ADC is 20 square units, then find the area of the triangle ABD.
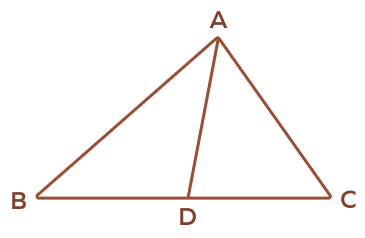
Solution:
Given: the area of the triangle ADC is 20 square units.
We know that the median of a triangle divides the triangle into two triangles having equal area.
Therefore, the area of the triangle ABD is also 20 square units.
- Determine the length of the median AM of the triangle ABC, whose sides are AB $= 4$ units, BC $= 5$ units, and AC $= 3$ units.
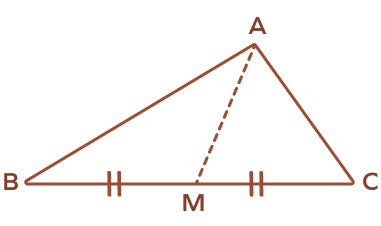
Solution:
Given: AB $= 4$ units $= c$
BC $= 5$ units $= a$
AC $= 3$ units $= b$
Here, we have to find the median AM of a triangle $(\text{i.e}.,\; m_{a})$. It can be calculated using the formula:
$m_{a} = \sqrt{\frac{2b^2 +2c^2\;-\;a^2}{4}}$
$\Rightarrow m_{a} = \sqrt{\frac{2(3)^{2} + 2(4)^{2}\;-\;(5)^{2}}{4}}\; = \sqrt{\frac{18 + 32\;-\;25}{4}}\; = \sqrt{\frac{25}{4}}\;= \frac{5}{2}$ units
Hence, the length of the median AM $= \frac{5}{2}$ units.
- Find the length of the median from the vertex A of a triangle ABC, whose vertices are A $(\;−\;1,\; 3)$, B $(1, \;−\;1)$, and C $(5,\; 1)$.
Solution:
Given: vertices of triangle ABC are A $(\;−1,\; 3)$, B $(1, \;−1)$, and C $(5,\; 1)$.
Step 1: Using the midpoint formula, find the midpoint of BC.
For any two points $(x_{1},\; y_{1})$ and $(x_{2},\; y_{2})$, midpoint is given by $\bigg(\frac{x_{1} + x_{2}}{2},\; \frac{y_{1} + y_{2}}{2}\bigg)$.
The midpoint of BC $= \bigg(\frac{x_{1}+x_{2}}{2},\; \frac{y_1+y_2}{2}\bigg)\;=\; \bigg(\frac{1+5}{2},\; \frac{-1 + 1}{2}\bigg) = (3, 0)$.
Let’s say midpoint as point D$(3,\; 0)$.
Step 2: Find the length of median AD using the distance formula.
For any two points $(x_{1},\; y_{1})$ and $(x_{2},\; y_{2})$, distance formula is given by $\sqrt{(x_{2}\;-\;x_{1})^{2} + (y_{2}\;-\;y_{1})^{2}}$
Hence, the length of median AD $= \sqrt{(3\;-\;(\;-1))^{2} + (0\;-\; 3)^{2}}\;=\;\sqrt{16 + 9}\; =\; \sqrt{25}\; = 5$
Hence, the length of median AD of triangle ABC $= 5$ units.
Practice Problems On Median of a Triangle
Median of Triangle: Definition with Examples
In which of the following triangles do the medians have different lengths?
In a scalene triangle, the medians have different lengths.
The centroid of a triangle is the meeting point of the _________.
The points where the medians of a triangle meet is known as the centroid.
Which line segment represents the altitude of $\Delta\text{ABC}?
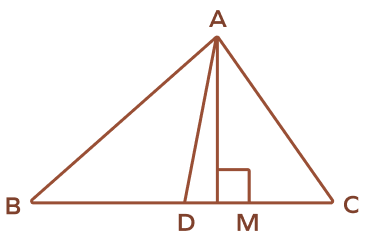
An altitude of a triangle is a line segment that starts from the vertex and meets the opposite side at right angles. In the given figure, AM is the altitude.
The three medians of a triangle divide the triangle into how many smaller triangles of equal area?
The three medians of a triangle divide the triangle into six smaller triangles of equal area.
For which of the following triangles are the medians and altitudes the same?
For an equilateral triangle, medians and altitudes are common.
Frequently Asked Questions On Median of a Triangle
What is the difference between the median and perpendicular bisector of a triangle?
In geometry, a line segment that joins vertices of triangles to the midpoints of opposite sides is called the median of a triangle. A line segment that intersects another line segment at a right angle and divides that other line into two equal parts at its midpoint is known as a perpendicular bisector.
What is the median of a right triangle?
In a right triangle, the median drawn from the vertex of the right angle is half the length of the hypotenuse.
What is the point of intersection of altitudes of a triangle called?
The points of intersection of altitudes of a triangle are called the orthocenter of the triangle.
What is incenter in a triangle?
The intersection point of all three interior angle bisectors of a triangle is the incenter. To put it another way, it can be described as the intersection of the triangle’s internal angle bisectors.
Are the medians of congruent triangles equal?
Yes, the medians of congruent triangles are equal because the corresponding parts of congruent triangles are congruent.



























