Mixed Numbers to Improper Fractions Conversion: Examples, FAQs

What Is Mixed Numbers to Improper Fractions Conversion?

A whole number and a proper fraction together create a mixed number. An improper fraction is a fraction in which the numerator is greater than the denominator.  

For instance, $\frac{2}{3}$ is a proper fraction since its denominator is bigger than its numerator, but $\frac{3}{2}$ is an improper fraction since “numerator $\gt$ denominator.”  

Any mixed number can be written in its improper fraction form and vice versa since they both basically represent the same fraction, just written in different forms. How can we turn a mixed number into an improper fraction? We will learn in this article! 

Mixed Fractions

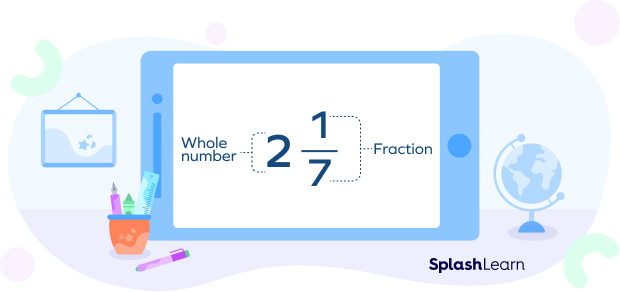
Mixed fraction is composed of a whole number and a proper fraction.

Example:  $2\frac{1}{7}$ is a mixed fraction, where 2 is the whole number part and $\frac{1}{7}$ is a proper fraction. This mixed number (or mixed fraction) lies between 2 and 3.

Improper Fraction

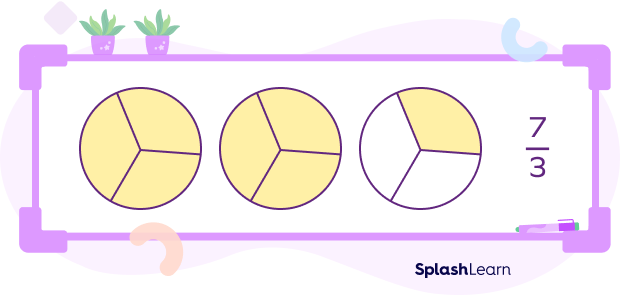
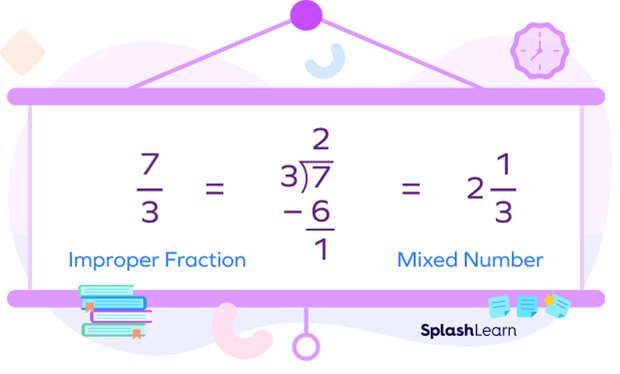
A fraction that has the numerator higher than or equal to the denominator is said to be inappropriate. For instance, $\frac{7}{3}$ is an improper fraction since the numerator 7 is bigger than the denominator 3.

The improper fraction $\frac{7}{3}$  is displayed below. Note that $\frac{7}{3}$ in the mixed number form is $2\frac{1}{3}$. Thus, you can see that there are 2 wholes and fraction $\frac{1}{3}$.

How to Convert a Mixed Number to an Improper Fraction

Let’s understand steps to convert a mixed number to an improper fraction with an example.

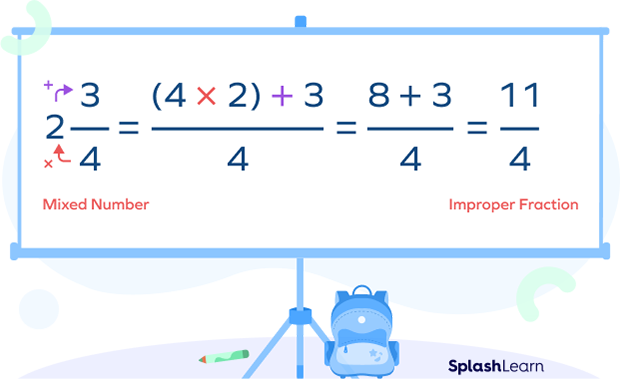
Example: Convert the mixed number $3\frac{4}{5}$ to improper fraction.

Step 1: Note down the whole number,  numerator, and denominator in the given mixed number.

Here, the whole number $= 3$, Numerator $= 4$, Denominator $= 5$

Step 2: Multiply the denominator with the whole number.

Here, multiply 5 and 3.

 $5 \times 3 = 15$

Step 3: Add the numerator to this product.

Add 15 and 4 (numerator): $15 + 4 = 19$

Step 4: This sum represents the numerator of the improper fraction. The denominator stays the same as the original fraction in the given mixed number.

Hence, $3\frac{4}{5} = \frac{19}{5}$.

How Do You Convert an Improper Fraction into a Mixed Fraction

Let’s understand steps to convert an improper fraction to a mixed number with an example.

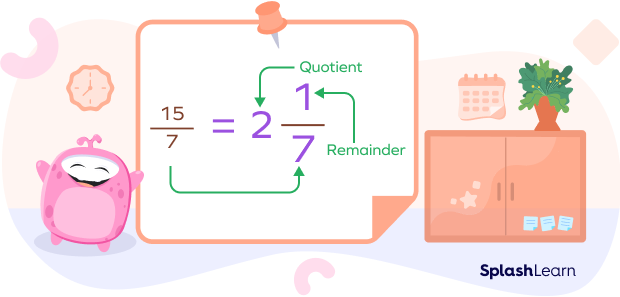
Example: Convert the improper fraction $\frac{15}{7}$ to a mixed number.

Step 1: Divide the fraction’s numerator by its denominator. Note down the quotient and the remainder. 

Here, we divide 15 by 7. 

We know that $(7 \times 2) + 1 =15$

Quotient $= 2$ and Remainder$ = 1$

Step 2: The quotient represents the whole number part of the mixed number. The remainder represents the numerator. The denominator stays the same.

 Thus, $\frac{15}{7} = 2\frac{1}{7}$

Example 2: Consider the improper fraction $\frac{7}{3}$.

Mixed Number to Improper Fraction Conversion Chart

Let’s take a look at a few examples of mixed number to improper fraction conversion. 

Mixed Number	Improper Fraction
$1\frac{1}{2}$	$\frac{3}{2}$
$2\frac{3}{4}$	$\frac{11}{4}$
$3\frac{5}{3}$	$\frac{14}{3}$
$7\frac{1}{2}$	$\frac{15}{2}$
$4\frac{6}{7}$	$\frac{34}{7}$

Adding Mixed Fractions

We can add mixed fractions easily by simply converting them into improper fractions.

Example: Find the sum: $4\frac{1}{3} + 5\frac{4}{3}$.

Convert both the mixed numbers to improper fractions.

$4\frac{1}{3} = \frac{(4 \times 3) + 1}{3} = \frac{13}{3}$

$5\frac{4}{3} = \frac{(5 \times 3) + 4}{3} = \frac{19}{3}$

Add the improper fractions by adding the numerators and keeping the same denominator.

$\frac{13}{3} + \frac{19}{3} = \frac{32}{3}$

Here, we can convert the improper fraction $\frac{32}{3}$ to a mixed number.

$\frac{32}{3} = 10\frac{2}{3}$

Thus, $4\frac{1}{3} + 5\frac{4}{3} = 10\frac{2}{3}$

When dealing with unlike fractions, we first find the Least Common Multiple (LCM) of the denominators and convert them to like fractions. They can then be added in the normal manner.

Example:  $1\frac{1}{2} + 2\frac{1}{3}$

$1\frac{1}{2} = \frac{(2 \times 1) + 1}{2} = \frac{3}{2}$

$2\frac{1}{3} = \frac{(3 \times 2) + 1}{3} = \frac{7}{3}$

Here, LCM $(2,3)\; = 6$

$1\frac{1}{2} + 2\frac{1}{3} = \frac{3}{2} + \frac{7}{3}$ 

                      $= \frac{9}{6} + \frac{14}{6}$ 

                      $= \frac{23}{6}$ 

                      $= 3\frac{5}{6}$

Subtracting Mixed Fractions

We can subtract mixed fractions by converting them into improper fractions. The steps are similar to steps of adding mixed fractions; only the operation is different.

Conclusion

In this article, we learned how to convert a mixed fraction to an improper fraction and vice versa. Let’s solve a few examples to understand the concept better.

Solved Examples on Mixed Number to Improper Fraction Conversion

1. Convert the mixed number $16\frac{2}{3}$ to an improper fraction.

Solution:

Multiply the denominator and the whole number.

 $3 \times 16 = 48$

Add the remainder to it.

 $48 + 2 = 50$

Numerator $= 50$

Denominator $= 3$

Thus, $16\frac{2}{3} = \frac{(16 \times 3) + 2}{3} = \frac{50}{3}$

2. Convert the improper fraction $\frac{17}{5}$ to a mixed number.

Solution: Given improper fraction $= \frac{17}{5}$

First, divide 17 by 5.

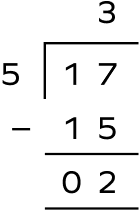
Quotient $= 3$ and Remainder $= 2$.

Thus, $\frac{17}{5} = 3\frac{2}{5}$ 

3. Convert the mixed number $1\frac{3}{7}$ to improper fraction.

Solution: 

$1\frac{3}{7} = \frac{(1 \times 7) + 3}{7}$

       $= \frac{7 + 3}{7}$

       $= \frac{10}{7}$

Improper fraction $= \frac{10}{7}$

Practice Problems on Mixed Number to Improper Fraction Conversion

Frequently Asked Questions on Mixed Number to Improper Fraction Conversion