Base of an Exponent – Definition with Examples

Base of an Exponent – Introduction

Wow, that’s a lot of zeros following the number 1. One million is a huge number! It can also be written as $10\times 10\times 10\times 10\times 10\times 10$. But there has to be a simpler way of writing it. We are in luck. The concept of “Base and Exponent” is mainly introduced to make reading and writing such huge numbers easier.

What is an Exponent in Math? 

An exponent shows how many times we multiply a number by itself. We can use them to represent not only very large numbers but also very small numbers. So, what is the base of an exponent? Let’s understand with an example.

Let us go back to the number we began with. One million, $1,000,000$, or $10\times 10\times 10\times 10\times 10\times 10$. Using exponents, this number is written as ${10}^6$. In ${10}^6$, the number 10 is called the base, and 6 is the exponent of the expression. So, the exponent is a number or letter written above and to the right of a mathematical expression, which is the base. 

To recap, the exponent of a number says how many times to use a base number in multiplication. It is written as a small number in the top right corner of the base number. We want to explore and know all about this base number. Let’s begin!

Base of an Exponent Definition

The base of an exponent is a number that is raised to a certain power. So, the base of an exponent represents the number that is multiplied by itself. 

The exponent represents how many times the base number is multiplied. 

The power can be defined as the number obtained by raising the base number to the exponent. So, it refers to the complete expression. 

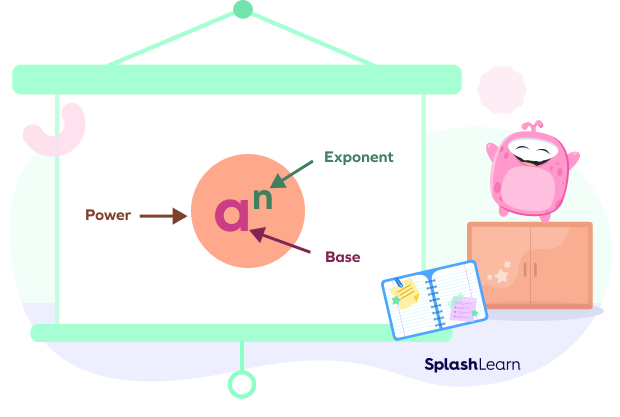
So, in the power $a^n$, the letter “a” is the base. The letter n is the exponent. 

It means that a is multiplied by itself n number of times.

Let us now look at some examples to understand the concept of ‘base of an exponent’ better.

Example:

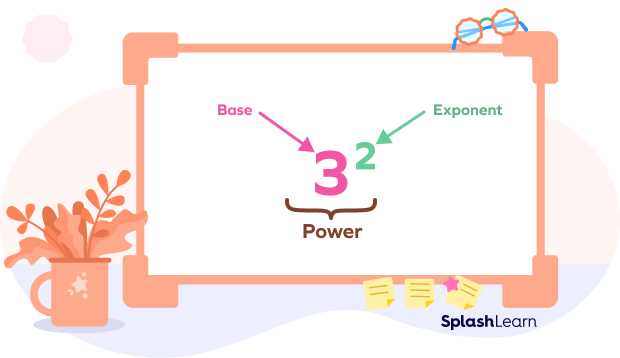
In $3^2$, 3 is the base, and 2 is the exponent. 

So, the power can be read as $8^3$. 

To get the solution for $8^3$, you can multiply 8 by itself three times.

$8^3=8\times 8\times 8=512$

$x^n$ can be read in many ways.

• x to the power of n
• x raised to n
• x to the n
• x to the nth power

Negative Bases

Let’s discuss examples where the base is negative.

We can discuss two cases here.

Case 1: If the base is negative and the exponent is an even number, the power is positive.

$(-5{)}^2=(-5)\times (-5)=25$ 

$(-2{)}^4=(-2)\times \times (-2)\times (-2)\times (-2)=16$

Case 2: If the base is negative and the exponent is an odd number, the power is negative.

$(-5{)}^3=(-5)\times (-5)\times (-5)=-125$

$(-2{)}^5=(-2)\times (-2)\times (-2)\times (-2)\times (-2)=-32$

Important Note: Be Careful!

$(-a{)}^n$ is not equal to $-a^n$.

$(-6{)}^2=(-6)\times \times (-6)=36$

Here, the base is $-6$.

 $-6^2=-(6\times 6)=-36$

Here, the base is 6.

Let’s summarize.

Negative Exponents

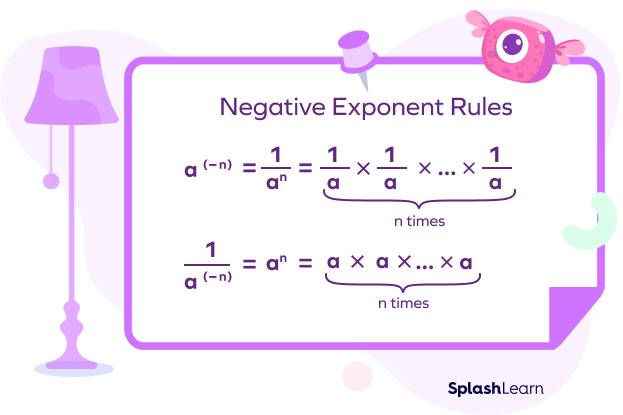
For a non-zero integer a, $a^{-}n$ represents the reciprocal of aⁿ, which equals $\frac{1}{a^n}$.

So, $a^{-}n$ is $\frac{1}{a}$ multiplied “n” number of times.

In other words, the negative exponent describes how many times we have to multiply the reciprocal of the base.

Examples:

${16}^{-}2=\frac{1}{16{-}^{-}2}=\frac{1}{16}\times \frac{1}{16}=\frac{1}{256}$

$\frac{1}{{10}^{-}3}={10}^3=10\times 10\times 10=1000$

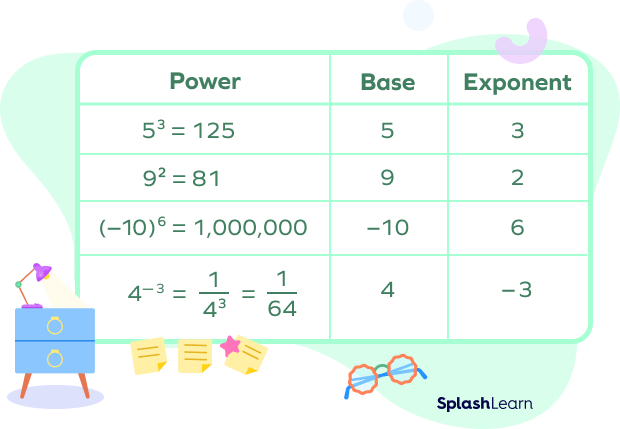
Take a look at a few more examples and revise the base, power, and exponents.

Interesting Facts about Exponents and Their Bases

• The word exponent was coined in 1544 by Michael Stifel.
• In the late sixteenth century, Jost Bürgi used Roman numerals for exponents.
• A base with 0 as its power is always equal to 1. 

Example: ${90}^{\circ }=1$

• Any number raised to the power 1 is always equal to that number.

Example: ${17}^1=17$

• $x^2$ is also read as x square and $x^3$ is also read as $x$ cube.

Solved Examples

1. Identify the bases and exponents of the following:

a) $2^9$

b) ${12}^{1}2$

c) $2^n$

Solution:

a) In $2^9,2$ is the base and 9 is the exponent.

b) In ${12}^{1}2$, the base and the exponent are the same: the number 12.

c) In $2^n,2$ is the base, and n is the exponent

2. What is the exponential form of the number 729? Identify its base and exponent.

Solution: 729 can be written as $3\times 3\times 3\times 3\times 3\times 3=3^6$

3 is the base, and 6 is the exponent

This means that the base 3 is multiplied by itself 6 times to equal 729.

3. Which is greater, the base 2 to the power of 6 or the base 6 to the power of 2?

Solution: The base 2 to the power of 6 is $2^6$. 

$2^6$ can be written as $2\times 2\times 2\times 2\times 2\times 2=64$

The base 6 to the power of 2 is $6^2$. 

$6^2$ can be written as $6\times 6=36$

Therefore, the base 2 to the power of 6 is greater than the base 6 to the power of 2.

So, $2^6>6^6$

4. Is $-9^2$ the same as $(-9{)}^2$? Explain why or why not.

Solution:

$-9^2$ is not the same as $(-9{)}^2$.

$-9^2=-(9\times 9)=-81$

Here, the base is 9.

$(-9{)}^2=(-9)\times (-9)=81$

Here, the base is $-9$.

5. What is the reciprocal of 49?

Solution: For a non-zero integer a, $a^{-}n$ represents the reciprocal of $a^n$, which equals $\frac{1}{a^n}$.So, the reciprocal of $4^9$ is $4^{-}9=\frac{1}{4^9}$.

Practice Problems

Frequently Asked Questions