Common Numerator – Introduction
When numbers are written as a fraction, they can be represented as $\frac{a}{b}$. Now the fraction has two main parts: the numerator and the denominator.
When the numerators of two or more fractions are the same or like, the fractions are said to have a like numerator, irrespective of whether the denominators are the same or not.
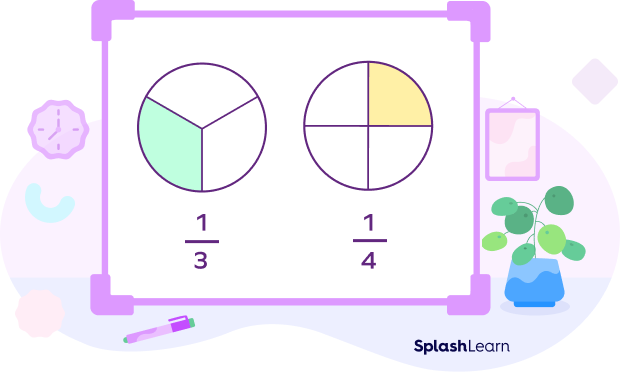
In the above example, the first figure is divided into 3 parts, and 1 part is shaded, whereas in the second figure, there are 4 equal parts, and only 1 is shaded. Thus, the fractions ⅓ and ¼ have like numerators.
When two or more fractions have different numerators, we can convert them into fractions with the same numerators by finding the common multiple of the numerators. Today, we will learn about the definition of Common Numerators and its facts. Let us get right into it.
Recommended Games
What Is a Common Numerator?
A common multiple of the numerators of two or more fractions is called a common numerator. Let’s study more by considering the following example.
Take the fractions $\frac{4}{5}$ and $\frac{6}{7}$. Both fractions have different numerators. To find their common numerator, we find the common multiples of the numerators 4 and 6.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, . . .
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, . . .
Common multiples of 4 and 6: 12, 24, 36, . . .
So, the least common numerator for 4⁄5 and 6⁄7 can be 12, 24, 36, . . .
If we want the common numerator to be 12, we must find the equivalent fraction of $\frac{4}{5}$ and $\frac{6}{7}$, which has 12 as the numerator.
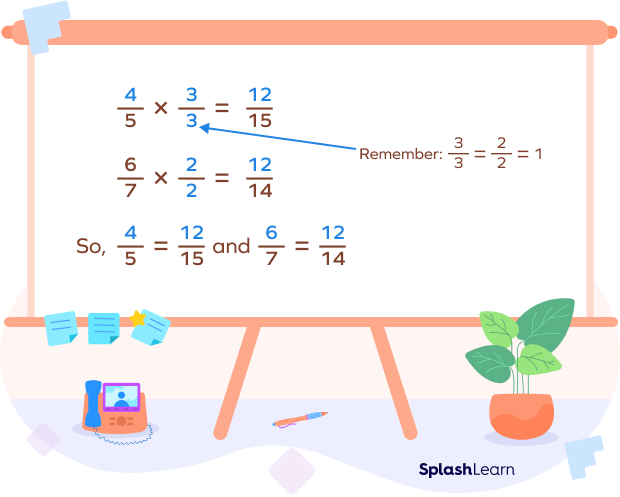
Now, we have two fractions with the same numerator.
So, $\frac{12}{15}$ and $\frac{12}{14}$ have a common numerator. It is 12.
So, now that we know how to find common numerators, how do we put them to use? How do they help us solve problems in fractions? Let’s take a look at some of the applications of common numerators. The most common use of it is to compare fractions. We can easily compare two or more fractions when their numerators are common or like. Let’s now figure out how we can do this.
Recommended Worksheets
Comparing Fractions with Like Numerators
We can use multiple strategies for comparing fractions. One of these is to compare the fraction by finding the common numerator strategy. Comparing fractions with like or same numerators is an easy task. For example, let us compare $\frac{2}{5}$ and $\frac{4}{7}$.
Look at the two numerators (4 and 2) and the two denominators (5 and 7). It is much easier to find a common multiple of the numerators (4) than to find a common denominator. So, find a fraction equivalent to $\frac{2}{5}$ with 4 as a numerator $(\frac{2}{5} \times \frac{2}{2} = \frac{4}{10} )$.
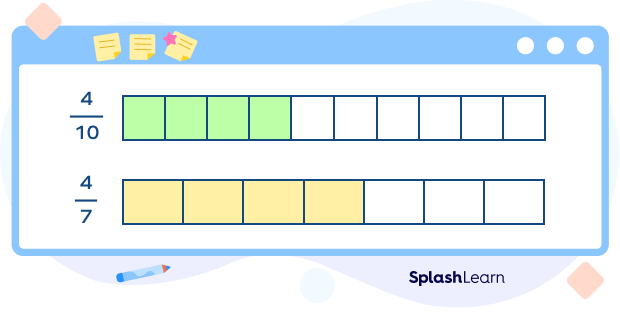
You can now compare $\frac{4}{10}$ and $\frac{4}{7}$ by comparing the size of each piece. Since sevenths are larger than tenths, $\frac{4}{7}$ is greater than $\frac{4}{10}$ or $\frac{2}{5}$ .
To compare two or more fractions with the same or like numerators, we just have to compare their denominators. The fraction with the smallest denominator is the greatest.
If we compare $\frac{8}{11}$ and $\frac{8}{17}$, we take a look at the denominators. Since 17 is more than 11. So, $\frac{8}{11}\gt\frac{8}{17}$.
Solved Examples
1. Identify which fractions have the same numerator.
$\frac{3}{8},\frac{7}{8}, \frac{3}{7}$ and $\frac{2}{7}$
Solution:
The fractions given are: $\frac{3}{8},\frac{7}{8}, \frac{3}{7}$ and $\frac{2}{7}$
Of these, the fractions $\frac{3}{8}$, and $\frac{3}{7}$ have the same numerator. Their numerators are like as they have the number 3 as the common numerator.
2. Find out the common numerator of $\frac{5}{8}$ and $\frac{7}{9}$.
Solution:
To find their common numerator, we find the common multiples of the numerators 5 and 7.
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, . . .
Multiples of 7: 7, 14, 21, 28, 35, 42, . . .
As we can seen, a common multiple of 5 and 7 is 35
So, a common numerator for $\frac{5}{8}$ and $\frac{7}{9}$ can be 35.
If we want the common numerator to be 35, we need to multiply both the numerator and denominator as shown:
$\frac{5}{8}\times \frac{7}{7} = \frac{35}{56}$
$\frac{7}{9} \times \frac{5}{5} = \frac{35}{45}$
Now, we have two fractions with the same numerator.
$\frac{35}{56} \gets$ common numerator $\to \frac{35}{45}$
3. Which fraction is greater: $\frac{5}{11}$ or $\frac{5}{13}$?
Solution:
The fractions $\frac{5}{11}$ and $\frac{5}{13}$ have the same numerator: 5. We know that if two or more fractions have like numerator, the fraction with the smallest denominator is the greatest. So, elevenths are greater than thirteenths.
Therefore, $\frac{5}{11} \gt \frac{5}{13}$.
4. Arrange the following fractions: $\frac{7}{11} ; \frac{7}{17}; \frac{7}{10}; \frac{7}{12}$
a) in the ascending order b) in the descending order
Solution:
The fractions $\frac{7}{11} ; \frac{7}{17}; \frac{7}{10}$ and $\frac{7}{12}$ have the same numerator: 7. We know that if two or more fractions have like numerators, the fraction with the smallest denominator is the greatest.
a) in the ascending order (smallest to greatest): $\frac{7}{17} \lt \frac{7}{12} \lt \frac{7}{11} \lt \frac{7}{10}$
b) in the descending order (greatest to smallest): $\frac{7}{10} \gt \frac{7}{11} \gt \frac{7}{12} \gt \frac{7}{17}$
Practice Problems
Common Numerator
What is the common numerator of these fractions: $\frac{7}{9} ; \frac{7}{11}; \frac{7}{12}$?
We know that the numerator is the part of a fraction that is above the fraction bar. So, the numerator of these fractions is 7.
Which of these fractions is the greatest?
We know that if two or more fractions have like numerators, the fraction with the smallest denominator is the greatest. Since 6 is the smallest, $\frac{5}{6}$ is the greatest of these fractions.
Choose the correct symbol to make the statement true.
$\frac{2}{7}$ ____ $\frac{4}{13}$
Look at the relationship between the two numerators (4 and 2). Let’s make the numerator the same or like by finding the common multiple of the numerators, which is 4.
$\frac{2}{7}=\frac{4}{14}$. Now compare the fractions $\frac{4}{14}$ and $\frac{4}{13} . \frac{4}{14} \lt \frac{4}{13}$
Which of the following fractions is greater than $\frac{3}{5}$?
If two or more fractions have a common numerator, then the fraction with the smallest denominator is the greatest. Here 4 is smaller than 5, making $\frac{3}{4} \gt \frac{3}{5}$.
Frequently Asked Questions
What does the numerator represent?
The numerator is the number that sits on the top of the fraction bar and represents the number of parts out of the whole. For example, in the fraction $\frac{18}{11}$, the number 18 is the numerator.
What is the numerator in the context of division?
In the context of division, the numerator is the dividend. We know that the number to be divided or distributed into a certain number of equal parts is called the dividend. Let us understand this with an example: If we were to divide the number 24 by 7 or $\frac{24}{7}$, the number 24 in this division is the numerator or dividend.
What is a common denominator?
In a fraction, a denominator represents the number of equal parts a whole is divided into. A common denominator is a common multiple of the denominators of two or more fractions. For example, consider the fractions $\frac{1}{8}$ and $\frac{1}{6}$. 24 is a common multiple of denominators 8 and 6. Thus, 24 is a common denominator of fractions $\frac{1}{8}$ and $\frac{1}{6}$.




































