Commutative Property of Multiplication – Definition With Examples

What Is the Commutative Property of Multiplication in Math? 

Commutative comes from the word “commute”, which can be defined as moving around or traveling. According to the commutative property of multiplication, changing the order of the numbers we are multiplying does not change the product.  

Let’s understand this with an example.

Example of Commutative Property of Multiplication

Place 3 bricks in a row.

Now place another row of bricks above this row. 

Repeat this process 4 times. 

 Now count the number of bricks used. 

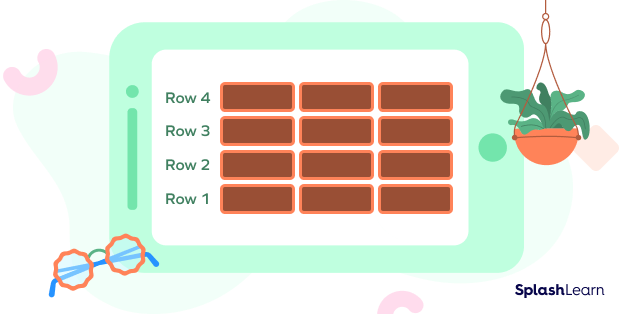
Total bricks $=$ Number of rows $\times$ Number of bricks in each row 

                    $=  4 \times 3$

                    $= 12$ 

Now, create a row by placing 4 bricks. 

Place two more rows above this row. 

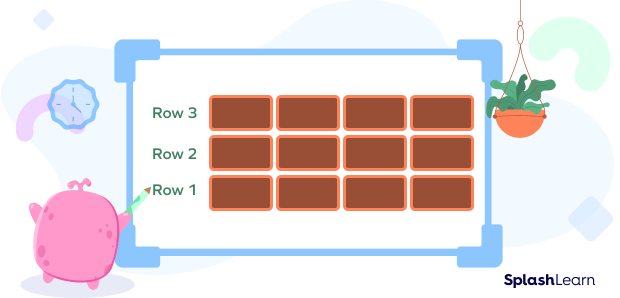
Total bricks $=$ Number of rows $\times$ Number of bricks in each row 

                    $=  3 \times 4$ 

                    $= 12$

We have observed that interchanging the number of rows with the number of bricks in each row does not change the total bricks needed. 

What Is Multiplication?

Multiplication is nothing but repeated addition. It is denoted by ‘*’, ‘.’ and ‘✕’.

Let’s see what is repeated addition with the help of given example:

Example: A monkey is jumping from one point to another. It covers one unit distance with every jump. How many units will it cover in 5 jumps?

Solution: From the above statement, we can say that 1 jump $= 1$ unit. Let’s look at this image. 

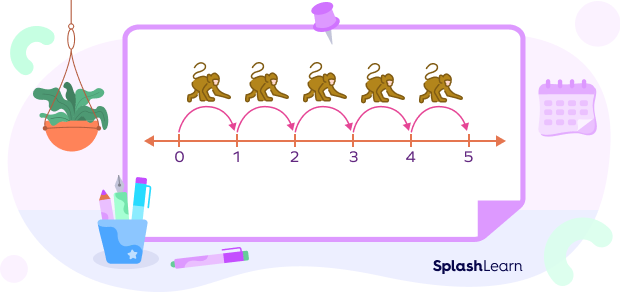
So, we can see that monkey covers $1+1+1+1+1 = 5$ units

We can also write it as $1 \times 5 = 5$ units.

Now, observe that for each step, we need to add “1” in the previous one. That’s why we can say that multiplication is nothing but repeated addition. 

Let’s go through another example. 

Example: Robin wants to buy 3 bars of chocolate. Each bar costs $\$$ 10. How much money Robin needs to buy 3 bars?

We can solve this problem using two different methods. Let’s look at both methods. 

Method 1:  

Number of chocolates  $\times$ Cost of Each Chocolate 

$= 3$ $\times $ $\$$ 10

$=$ $\$$ 30

Method 2 :  

Cost of Each Chocolate $\times$ Number of chocolates

 $=$ $\$$ 10 $\times$ $3$ 

  $=$ $\$$ 30

We have observed that  the order in which we multiplied the number of chocolate bars and cost of each bar does not change the amount required.

Commutative Property of Multiplication 

You must be familiar with tables up to 5.

Have you observed 

$1 \times 2  = 2  \times 1 = 2$

$2 \times 4  = 4  \times 2 = 8$ 

$3 \times 5  = 5  \times 3 = 15$

So, we can conclude that the order in which we multiply numbers does not change the final answer.

Do you know? 

If you remember tables up to 5, you can figure out the multiplication of bigger tables by using the commutative property. 

For example:

If you know 

Five times eight, i.e., $5 \times 8 =$ ? 

You can also answer 

Eight times five, i.e., $8 \times 5  =$ ? 

Both are equal to 40. 

Fact to Remember

The commutative property applies only to addition and multiplication but not to subtraction and division. 

Let’s understand this with examples. 

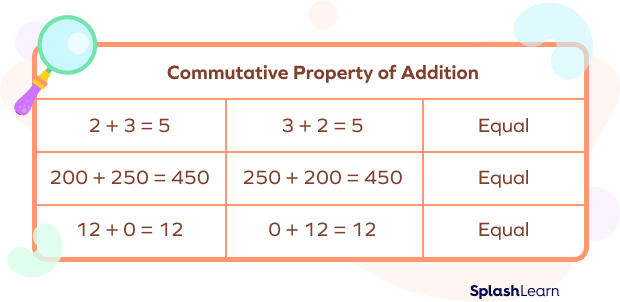
Alt Tag: Commutative Property holds true in case of Multiplication

So, we can conclude that commutative property applies to addition and multiplication, not to subtraction and division.

Conclusion

In conclusion, we can say that

• Multiplication is nothing but the repeated addition.
• Commutative property means the end result will not change if we change the order.
• Multiplication and addition follows commutative property.

Solved Examples

Example 1: Fill in the blanks. 

1. $4 \times 5 = 5 \times \underline{}$

      Solution:   $4  \times  5  =  5 \times  4$

2. $3 \times = 6 \times \underline{}$

Solution:  $3 \times \underline{} $6$ \underline{} = 6 \times 3$

3. $2  \times  1  = 1  \times \underline{}$

Solution:  $2  \times  1  = 1  \times  2$

4. $3 \times 6 \times \underline{} =  3 \times 2 \times 6$

      Solution:  $3 \times 6 \times 2 =  3 \times 2 \times 6$ 

5. $16 \times 2 \times  4 =  2 \times \underline{} \times  4$

Solution:  $16 \times 2 \times 4 =  2 \times 16  \times  4$

6. $9 \times \underline{} \times  2  =   8 \times \underline{} \times 2$ 

      Solution: $9 \times \underline{} 8 \underline{} \times 2  =   8 \times 9 \times 2$

Example 2: Complete the following statement:

The commutative property says that the order of numbers in _________ and _________ does not change the result.

Solution: 

The commutative property says that the order of numbers in multiplication and addition does not change the result.

Only multiplication and addition follow the commutative property.

Practice Problems

Frequently Asked Questions