Definition of Inverse?
In mathematics, the word inverse refers to the opposite of another operation.
Let us look at some examples to understand the meaning of inverse.
Example 1:
The addition means to find the sum, and subtraction means taking away. So, subtraction is the opposite of addition. Hence, addition and subtraction are opposite operations. We may say, subtraction is the inverse operation of addition.
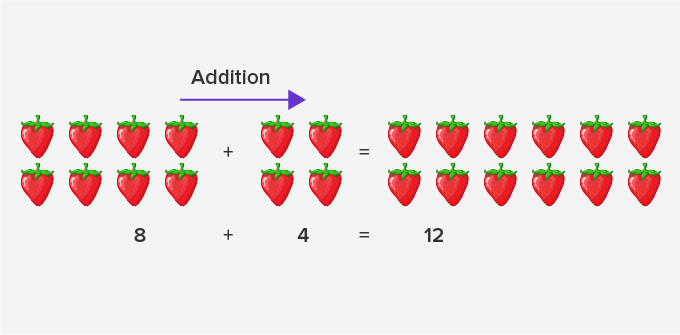
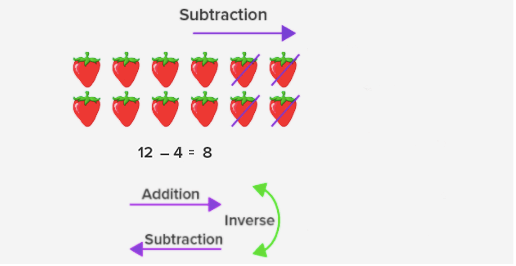
Example 2:
Multiplication is repeated addition. The same number gets added repeatedly.
However, the division is repeated subtraction. The same number gets subtracted repeatedly. So, division is the opposite of multiplication. Hence, multiplication and division are opposite operations. We may say, division, is the inverse operation of multiplication.
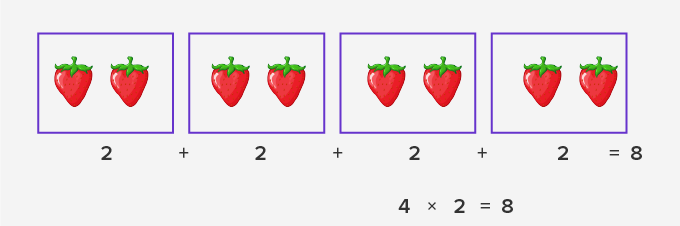
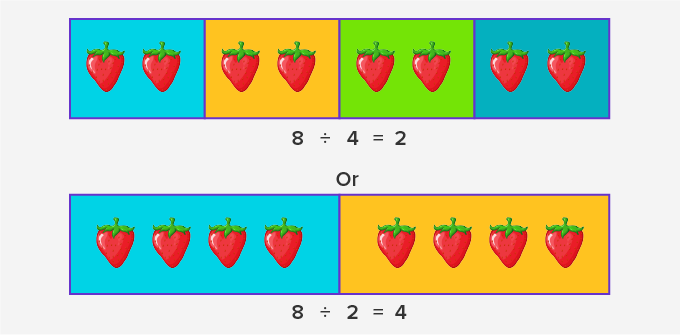
So, we see that multiplication and division are inverses of each other.
Recommended Games
Multiplicative Identity:
A multiplicative identity is a number that when multiplied by any non-zero number gives the same number as the product.
For example, if a is any non-zero number, then multiplying a by 1 gives the product as the number itself.
a × 1 = a
Therefore, 1 is the multiplicative identity.
Recommended Worksheets
Multiplicative Inverse:
A multiplicative inverse is a number which when multiplied by a number gives 1 (multiplicative identity) as the product.
If a is any non-zero number, then multiplying a by what number gives the product as 1?
a × ? = 1
As, a⁄a = 1, we need a number in which a is in the denominators place. We have a in the numerator. So, we keep 1 is the numerator of this number and get 1⁄a.
a × 1⁄a = 1
So, 1⁄a is the multiplicative inverse of a.
Multiplicative inverse is also called a reciprocal.
Reciprocal of a number is obtained by interchanging its numerator and denominator.
The multiplicative inverse of a is 1⁄a and multiplicative inverse of a fraction a⁄b is b⁄a

| Fun Facts – Inverse property is also seen in proportion. It is called the inverse proportion. In inverse proportion, when one value increases the other decreases. For example, if the number of machines increases, the time taken to complete the task decreases. |
Practice Problems
Inverse Operation
Which of the following would be the multiplicative identity for the decimal number 2.35?
The multiplicative identity is a quantity which when multiplied by any number gives the product as the number itself. The only number that follows this condition is the number 1.
Identify the related division sentence for 5 × 2 = 10.
Here, as per the given multiplication expression, 5 and 2 are the factors of 10.
Hence 10 divided by 2 equals 5 or 10 divided by 5 equals 2 are the only plausible division sentences for the given equation.
What is the multiplicative inverse of 2/3?
2/3 × 3/2= 1.
Hence, the multiplicative inverse of 2/3 = 3/2.
Find the multiplicative inverse of 7.
We need to find a number which when multiplied by 7 would give the result as 1.
7 × 1/7= 1. Hence, the multiplicative inverse of 7 is 1/7.
Frequently Asked Questions
What are inverse operations?
Operations that are opposite of each other are known as inverse operations. For example, division is the inverse operation of multiplication and subtraction is the inverse operation of addition.
What are some examples of inverse operations?
Multiplication and Division: 3 ✕ 4 = 12 and 12 ÷ 4 = 3. Addition and Subtraction: 8 + 2 = 10 and 10 – 2 = 8.
Are multiplicative inverse and inverse operations the same thing?
No, multiplicative inverse and inverse operations are not the same things. To begin with, the multiplicative inverse of a number is division of 1 by that number (e.g., 5 and ⅕). Inverse operations are opposite operations that undo each other. For example, 5 ✕ 2 = 10 and 10 ÷ 2 = 5 are inverse operations.
When do we use inverse operations?
Inverse operations are used in solving algebraic equations. For example, to separate a variable from its coefficient (the number it is multiplied by) in a linear equation (e.g., 3x = 12), we divide both sides of the equation by that coefficient.




































