What Is Long Multiplication?
Long multiplication is a method of multiplying large numbers easily. It simplifies the process of multiplication of two numbers that are not otherwise easy to multiply.
For example, we can easily find the product of $55 \times 20$ by multiplying 55 by 2 and then adding a 0 at the rightmost place of the answer.
$55 \times 2 = 110$ and $55 \times 20 = 1100$
However, sometimes, finding the product is not this easy. In such cases, we use the method of long multiplication. It is often termed as the long hand multiplication (long multiplication by hand).
Long Multiplication: Definition
Long multiplication is a method of multiplication using which multiplying two large numbers that have two or more digits becomes easier.
For example, we can easily find the product of $55 \times 20$ by multiplying 55 by 2 and then adding a 0 at the rightmost place of the answer.
$55 \times 2 = 110$ and $55 \times 20 = 1100$
But how to multiply large numbers? Many times, finding the product is not this easy. In such cases, we use the long method of multiplication.
For example: $47 \times 63 =$ ?
We can find the answer in simple steps using long multiplication. Let’s discuss the method in detail in the next section.
Recommended Games
How to Multiply Using Long Multiplication
Let’s discuss the steps for multiplying a two-digit number by a two-digit number using the long multiplication method.
Let us multiply 47 by 63 using the long multiplication method.
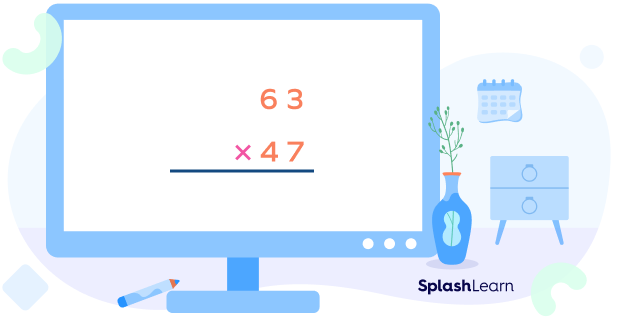
Step 1: First, write the two numbers, one below the other, such that their place values are aligned. We generally write the bigger number on top and a multiplication sign on the left and draw a line below the numbers as shown below.
Important Note:
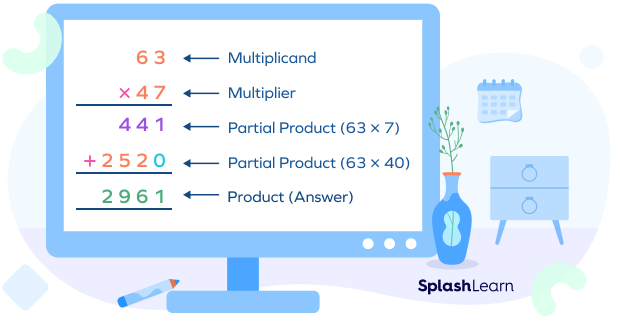
- In the long multiplication method, the number on the top (63) is called the multiplicand. The number by which it is multiplied, that is, the number at the bottom (47), is called the multiplier.
- If you write the small number on the top and perform the multiplication, the answer will still be the same since the order does not matter while multiplying two numbers.
Step 2: Multiply the ones digit of the top number by the ones digit of the bottom number.
Write the product as shown in the image. Don’t forget the carryover that goes in the next place!
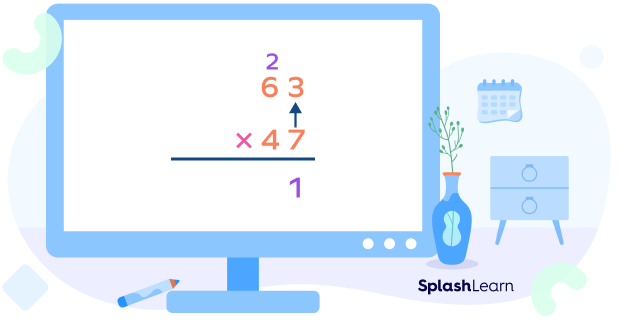
Step 3: Multiply the tens digit of the top number by the ones digit of the bottom number. Add the carryover.
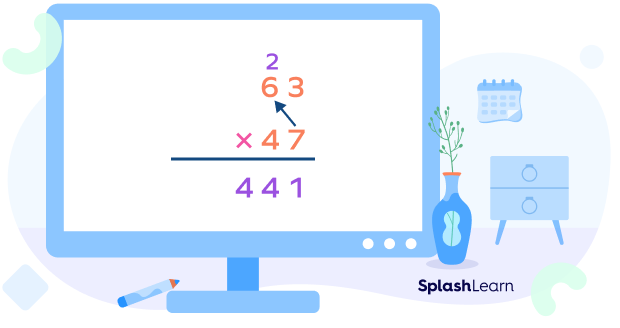
This is our first partial product which we got by multiplying the top number by the ones digit of the bottom number.
Step 4: Now, we place a 0 below the ones digit as shown. This is because we will now be multiplying the digits of the top number by the tens digit of the bottom number.
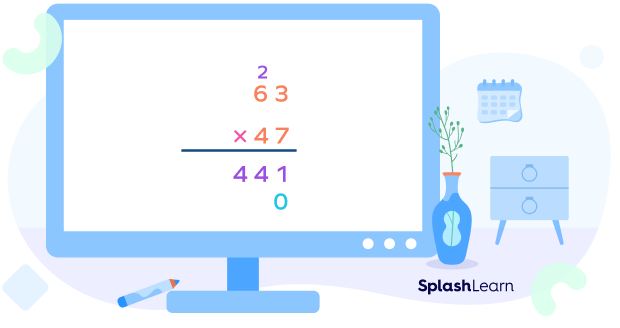
Step 5: Multiply the ones digit of the top number by the tens digit of the bottom number.
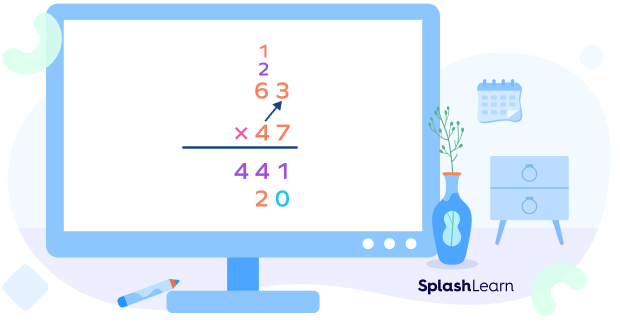
Step 6: Multiply the tens digit of the top number by the tens digit of the bottom number.
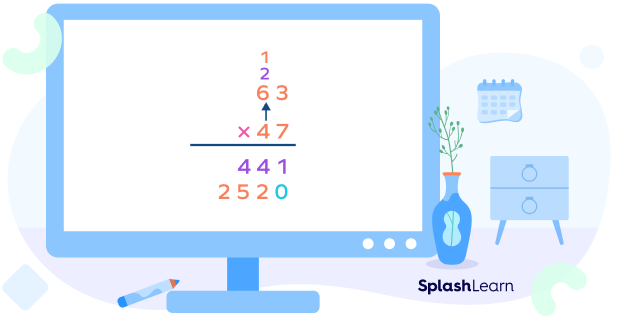
This is the second partial product obtained by multiplying the top number by the tens digit of the bottom number.
Step 7: Now, add the two partial products.
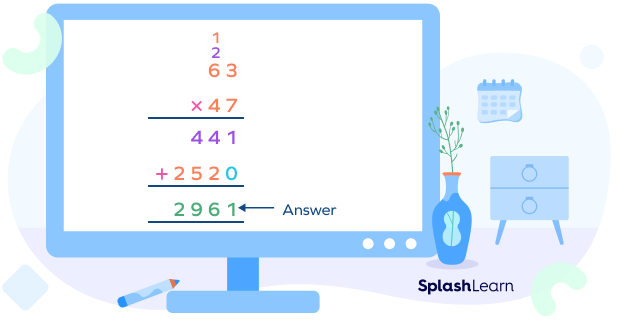
Let’s summarize.
We follow the above long multiplication steps only for multiplying numbers greater than two digits.
Recommended Worksheets
Long Multiplication Column Method
Long multiplication is also known as the column method of multiplication since we perform the multiplication vertically or column wise.
Let’s take another example to understand this better.
Multiply 321 by 23.
Take a look at the long multiplication chart that shows the long multiplication step by step. You can refer to it to avoid mistakes when solving long multiplication problems.

Multiplying Decimals Using Long Multiplication
Let’s understand how to multiply decimals with the help of the long multiplication method.
Example: Multiply $3.6 \times 5.5$
Step 1: First, we place the smaller number out of the two on the right-hand side and change the decimal number to a fraction.
$5.5 \times 3.6 = \frac{55}{10} \times \frac{36}{10}$
Step 2: Then, we multiply the numerators using the steps of the long multiplication method. We leave the denominator as it is for now.

Step 3: Now, we divide the answer (that we got in step 2) by the denominator to get the final answer.
$\frac{1980}{100} = 19.80$
Long Multiplication Using the Horizontal Method
Let’s now understand how to use the horizontal method with the help of a long multiplication example. As the name suggests, we multiply the numbers horizontally but follow the same steps as we discussed earlier.
Example: Multiply 48 by 24.
Step 1: First, we write the numbers beside each other and place them horizontally.
$48 \times 24$
Step 2: Now, we multiply the second number (number on the right side) with the ones digit of the first number.
Here, we multiply 24 with 8, since 8 is at the ones place in 48.
$24 \times 8 = 192$
Step 3: Now, we multiply the second number with the tens digit of the first number.
Here, we multiply 24 with 40, since 4 is at the tens place in 48.
$24 \times 40 = 960$
Step 4: Finally, we add the partial products obtained from steps 2 and 3 to get the final answer.

Thus, $48 \times 24 = 1152$
Long Multiplication with Negative Numbers
The multiplication of negative numbers using the method of long multiplication follows the same steps as mentioned above. However, we have to carefully consider the signs of the two numbers in order to decide the sign of the product.
For instance, when we multiply two negative numbers with each other, the sign of the result remains positive. On the other hand, it becomes negative when a negative number and a positive number are multiplied.
The figure below shows how the sign changes upon multiplication with negative numbers:

Fun Facts about Long Multiplication
- Long multiplication is also known as the column method of multiplication.
- Whenever any number is multiplied by zero, the answer is also zero.
- When the number 9 is multiplied by any other number, the sum of digits in the product is always 9.
For example, $9 \times 25 = 225$ and $2 + 2 + 5 = 9$;
$9 \times 9 = 81$ and $8 + 1 = 9$.
- Long multiplication can also be referred to as repeated addition because multiplying any number is just an alternative to adding it repeatedly.
- Whenever any even number from 0 to 9 is multiplied by 6, the product has the same even number in the ones digit.
For example, $6 \times 4 = 24,\; 6 \times 2 = 12$
- Whenever two large numbers (let’s say three-digit or four-digit numbers) are multiplied, the process of long multiplication remains the same. For example:

Conclusion
Long multiplication is a method that simplifies the multiplication of large numbers, including two-digit, three-digit numbers, etc., with each other. Let’s solve a few examples and practice problems based on long multiplication!
Solved Examples on Long Multiplication
1. Multiply 38 by 91 using the column method.
Solution:
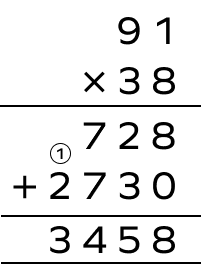
2. Multiply 72 by 44 using the column method.
Solution:

3. Multiply –58 by 30.
Solution:
The sign of the product when we calculate $(\;-\;58) \times (30)$ will be negative.
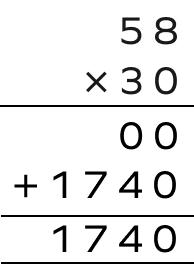
Since 58 has a negative sign, the final answer will be $–1740$.
$(\;-\;58) \times (30) = \;-\;1740$
4. Alia bought 42 notebooks, each worth $\$9.6$. How much did she spend?
Solution:
To find the amount Alia spent, multiply 9.6 by 42.
$9.6 \times 42 = \frac{96}{10} \times 42$
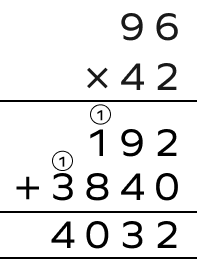
Now, we divide 4032 by 10 to get the final answer, which is $403.2$.
$9.6 \times 42 = 403.2$
Thus, Alia spent $403.2 on notebooks.
5. Multiply $-70$ and $-15$.
Solution:
Let’s find $(70) \times (15)$.
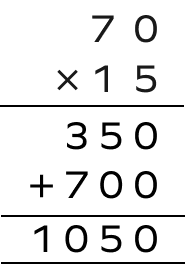
Since both the numbers are negative, the final answer will remain positive, $1050$.
$(70) \times (15) = 1050$
Practice Problems on Long Multiplication
Long Multiplication: Definition with Examples
Multiply 95 by 13 using the column method.
$95\times13 = 1235$
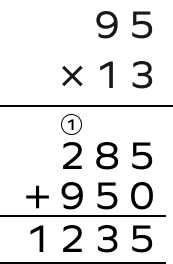
Multiply the decimals 1.2 and 6.7.
$6.7\times1.2=\frac{67}{10}\times\frac{12}{10}$
First, we multiply the numerators. Then, we divide their product with the denominators to reach the final answer.
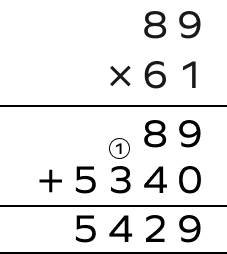
Multiply the negative numbers $(-\;89)$ and $(-\;61)$.
Since both the numbers are negative, the final answer will remain positive.
$(-\;89)\times(-\;61) = 5429$.
Multiply 45 by 21 using the horizontal method.
$21\times5=105$ __(i)
$21\times4=84$ __(ii)
Adding (i) and (ii), we get
$105\;+\;84=945$.
Multiply 530 by 22.
$530\times22 = 11660$
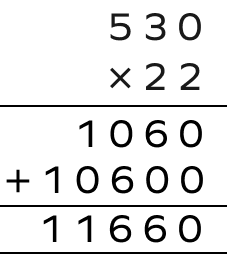
Frequently Asked Questions on Long Multiplication
What are negative numbers?
Negative numbers are those whose value is less than zero and thus have a negative sign (-) before them.
What are positive numbers?
Positive numbers are those whose value is greater than zero.
What is a decimal?
A decimal number represents the number that separates a whole number from a fractional number. It is represented by a dot (.) sign.
What is the meaning of the horizontal method of multiplication?
The horizontal method refers to a method wherein numbers are arranged in a horizontal line from left to right.
What is the meaning of the column method of multiplication?
The column method refers to a method wherein numbers are placed one below the other from top to bottom.
What is short multiplication?
Short multiplication is the method of multiplication commonly used when multiplying a three-digit or larger number with a single-digit number.




































