Multiplication Property of Inequality: Introduction
An algebraic equation is a mathematical statement that has two sides (LHS and RHS) separated by the “equal sign $(=)$.” The multiplication property of equality states that equality holds when the both sides of an equation are multiplied by a common value.
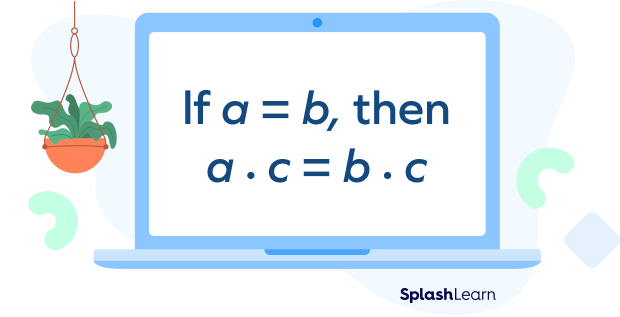
Recommended Games
Multiplication Property of Equality: Definition
Multiplication property of equality states that if both the sides of an equation are multiplied by the same number, the expressions on the both sides of the equation remain equal to each other.
Consider the algebraic equation $a = b$, where a and b are real numbers.
Let’s multiply both sides by the real number c.
By the multiplication property of equality, we get
Recommended Worksheets
What Is the Property of Equality?
The properties of equality describe the relation between two equal quantities. If any mathematical operation is applied on one side of an equation, then it must be applied on the other side of an equation to keep it balanced.
In other words, the properties that do not change the truth value of an equation or, the properties that do not impact the equality of two or more quantities are called the properties of equality.
Such properties of equality help in solving various algebraic equations and define an equivalence or balance relation.
What Is the Multiplicative Property of Equality?
According to this property, when we multiply the same real number on both the sides of an equation, then the two sides of the equation always remain equal.
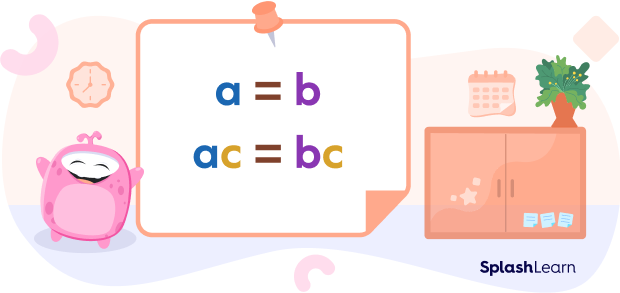
We can express the formula for this property as, for real numbers a, b, and c,
if $a = b$, then $a \times c = b \times c$.
This fact is used in arithmetic to find the equal terms. In algebra, the multiplicative property of equality helps us to isolate an unknown term from an equation. This is because multiplication and division are inverses of each other.
Example 1: Suppose that Lisa and Linda have the same amount of money, $\$100$ each. If both of them triple their amount of money, that is both of them multiply their money by 3; they still have the same amount of money, $\$300$ each.
We can also use this property to solve equations.
Example 2: $\frac{x}{4} = 5$
If we multiply both the sides by 4, the equality still holds and we get
$\Rightarrow \frac{x}{4} \times 4 = 5 \times 4$
$\Rightarrow x = 20$
To check we can substitute the value of $x$ in the original equation.
$\frac{20}{4} = 5$
$5 = 5$
Example 3: One-fourth of the kids who visited the amusement park “Jump & Slide” on holiday tried their new ride “loop-O-loop.” If 75 kids tried the ride, how many kids visited the park that day?
Let “a” be the number of kids who visited the park that day. One-fourth of this number is given to be 75. That is,
$\frac{a}{4} = 75$
We need to solve the equation for a.
By the multiplication property of equality, if we multiply both sides by the same number, the equality still holds true. So, multiplying both sides by 4.
$\frac{a}{4} \times 4 = 75 \times 4$
$a = 300$
Therefore, the 300 kids visited the park that day.
Converse of the Multiplication Property of Equality
Converse of the multiplication property of equality holds true. It can be stated mathematically as:
Let $a,b$ and $c$ be real numbers.
If $a \neq b$, then $a \times c \neq b \times c$
Or
If $a \times c = b \times c$, then $a = b$
Multiplication Property of Equality with Fractions
Let’s understand the multiplication property of equality for fractions. For any non-zero number a, the multiplicative inverse is nothing but the reciprocal $\frac{1}{a}$ such that $a. \frac{1}{a} = 1$.
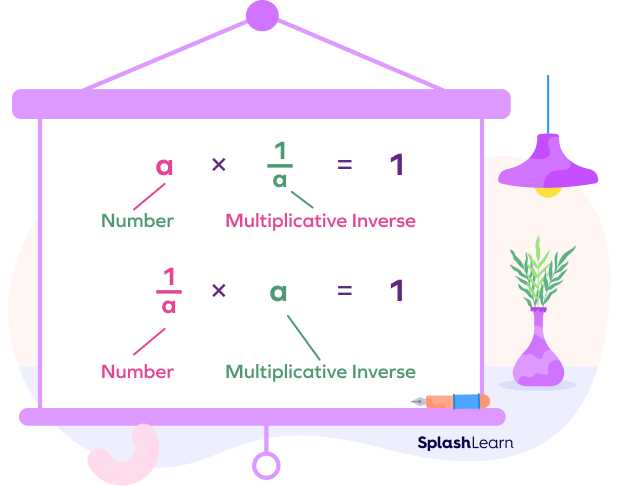
The multiplicative inverse property, which states that any number, other than 0, multiplied by its reciprocal will give a result of 1.
Let’s see an example of multiplicative property of equality.
$\frac{3}{2} y = 9$
Eliminating the fraction by multiplying both the sides by the multiplicative inverse.
$\frac{3}{2} \times \frac{2}{3} y = 9 \times \frac{2}{3}$
Using the multiplicative inverse will result in 1 on the left side.
$1 y = 6 \Rightarrow y = 6$
Fun Facts!
1. Another form of the property is if $a, b, c$, and d are real numbers such that $a = b, c = d$, then $ac = bd$.
2. Since division is the multiplication by the reciprocal if a,b and c are real numbers such that $a = b$ and $c \neq 0$, then $a \times \frac{1}{c} = b \times \frac{1}{c}$ or $\frac{a}{c} = \frac{b}{c}$. This is also known as the division property of equality.
Conclusion
In this article, we learnt about the multiplicative property of equality. Multiplicative property of equality states that if we multiply the same number on both sides of an equation, then the equation remains balanced.
Solved Examples
1. Let $a$ and $b$ be real numbers such that $\frac{z}{2} = 3 x$ and $\frac{z}{3} = 2 z$,
then show that $x = z$.
Solution: $\frac{z}{2} = 3 x$,
Multiplying both the sides by 2.
$\frac{z}{2} \times 2 = 3x \times 2$
$z = 6 x$
Substituting the value of $z$ in $\frac{z}{3} = 2 z$
$\frac{6x}{3} = 2 z$
$2 x = 2 z$
2. If $\frac{3x}{4} = 36$, then find the value of $x$.
Solution: $\frac{3x}{4} = 36$
Multiplying both the sides by the multiplicative inverse of $\frac{3}{4}$ i.e. $\frac{4}{3}$.
$\frac{3x}{4} \times \frac{4}{3} = 36 \times \frac{4}{3}$
$x = 48$
3. If $2(m + 3) = 12$, then find the value of $m$.
Solution: $2(m + 3) = 12$
$2(m + 3) = 2 \times 6$
We know that if $ac = bc$, then $a = b$ if $c \neq 0$.
$m + 3 = 6 \Rightarrow m = 6 − 3 = 3$
4. Solve for $y: \frac{y + 8}{2} = − 7$
Solution: $\frac{y + 8}{2} = − 7$
Multiplying both the sides by $2$
$2 \times ( \frac{y + 8}{2} ) = − 7 \times 2$
$y + 8 = − 14$
$y = − 22$
5. If $\frac{3n + 5}{4} = 15$, then find the value of $n$.
Solution: $\frac{3n + 5}{4} = 15$
Multiplying both the sides by $4$
$4 \times \frac{3n + 5}{4} = 15 \times 4$
$3 n + 5 = 60$
$3 n = 55$
$n = \frac{55}{3} = 18\frac{1}{3}$
Practice Problems
Multiplication Property of Equality - Definition with Examples
One seventh of the students in a class are boys. If the number of boys in the class is 21, then how many girls are there in the class?
Let total number of students be $x$.
$\frac{x}{7} = 21 \Rightarrow x = 147$
Number of girls $= 147 – 21 = 126$
Which property of equality can we use to solve the equation $\frac{x}{3} = 16$?
In order to solve for $x$, we will multiply both sides by 3.
If $a = b$, then which of the following is incorrect regarding the multiplicative property of equality?
$a + 2 = b + 2$ shows the additive property of equality.
Two-third of the total eggs are defective. If the number of non defective eggs is 24, then find the total number of eggs.
Let the total number of eggs be $x$.
$x − \frac{2x}{3} = 24 \Rightarrow \frac{x}{3} = 24$
Multiplying both the sides by 3, we get
$x = 72$
Find the value of $x$ if $\frac{x}{6} = 12$
$\frac{x}{6} = 12$
Multiplying both the sides by 6, we get
$\frac{x}{6} \times 6 = 12 \times 6 \Rightarrow x = 72$
Frequently Asked Questions
How is the multiplicative property of equality different from the commutative property of multiplication?
According to multiplicative property of equality, if $a = b$, then $ac = bc$ where $a,b,c$ are real numbers. On the other hand, according to the commutative property of multiplication, $a \times b = b \times a$.
What is the difference between the multiplicative property of equality and division property of equality?
According to multiplicative property of equality, if $a = b$, then $ac = bc$ where $a,b,c$ are real numbers and $c \neq 0$. On the other hand, division property of equality states that if $a = b$, then $\frac{a}{c} = \frac{b}{c}$ where $a,b,c$ are real numbers and $c \neq 0$.
What is the multiplicative property of inequality?
If $a \lt b$ and if $c$ is a positive number, then $a \times c \lt b \times c$.
If a $\lt$ b and if c is a negative number, then $a \times c \gt b \times c$.
When a and b are multiplied by the same negative number, the inequality reverses.
How is the multiplicative property of identity different from the multiplicative property of equality?
According to the multiplicative property of identity, any number multiplied by 1 gives the same result as the number itself. Whereas, according to multiplicative property of equality, if $a = b$, then $ac = bc$ where $a,b,c$ are real numbers.
Why can’t $c = 0$ in the multiplicative property of equality?
Well, $c \neq 0$ in the multiplicative property of equality because multiplying by zero can change the truth of an equation. It can take a false equation to a true equation.




































