Suppose you are at the bakery and you want to buy four cupcakes. When you reach there, you see that one cupcake costs $5. How will you calculate how much you should pay at the check-out counter?
The concept of product in math helps you answer this and do much more!
What is Product in Math?
A product in math is defined as the result of two or more numbers when multiplied together.
Let us consider the same scenario. You were running an errand at the bakery and had to buy 4 cupcakes. Each cupcake costs $5.
To calculate the total amount you need to pay at the checkout counter, you can add the cost of each cupcake 4 times (as you need to buy 4 cupcakes).

So, the answer will be
5 + 5 + 5 + 5 = $\$$20
If you needed 10 cupcakes, you would have to add the cost 10 times.
This is where the concept of multiplication and product can help you.
In the previous answer, you can calculate the cost of 4 cupcakes by simply multiplying them,
You can find the cost as,
4 times 5 or 4 ✕ 5,
You can skip count by 5, four times and get the answer as 20.
Recommended Games
Multiplier, Multiplicand, and Product
A multiplicand is the number of objects in a group, and a multiplier is the number of such equal groups. Let’s consider an example to understand this better.
Suppose you have 3 baskets, and each basket has 6 oranges. How will you calculate the total number of oranges?
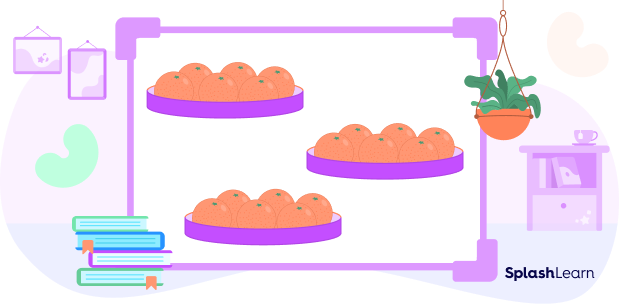
This is when the concept of the product comes to our rescue! First, let us write this as a multiplication expression as:
Number of groups ✕ number of objects in each group
or
3 ✕ 6
So, we can find the total number of oranges by skipping counting by 6, three times, and that is 18.
So we get, 3 ✕ 6 = 18.
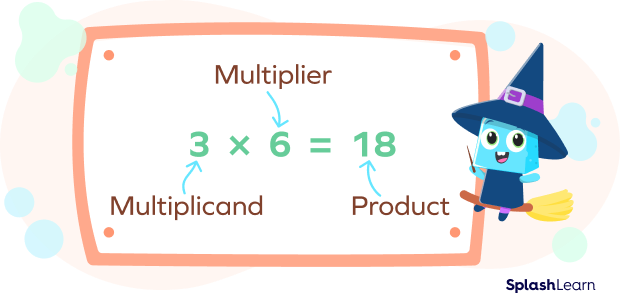
This is a multiplication expression. A multiplication expression has three parts, a multiplier, a multiplicand, and the product.
Recommended Worksheets
Commutative Property of Product
Interestingly, if the order of the multiplicand and multiplier are reversed, the product remains the same:
Let’s look at an example:
2 ✕ 3 = 6
Here, 2 is the multiplicand, 3 is the multiplier, and 6 is the product.
If we reverse the equation, we still get
3 ✕ 2 = 6
Fascinating, isn’t it?
Product of Fractions and Decimals
So far, we have learned how to calculate the product of whole numbers. Let’s now learn how to find the product of fractions and decimals!
Product of Fractions
Let’s learn this with the help of an example.
Suppose we have to find the product of the fractions 52 and 34.

Step 1: Multiply the numerator with the numerator and the denominator with the denominator.

Step 2: If you get an improper fraction, you can convert this into a mixed number.

We can also find the product of two mixed numbers or a fraction and a mixed number or even a whole number and a fraction by the same method by just ensuring that we convert our multiplicand and multipliers into fraction form first.
Product of Decimals
What makes a decimal number special?
The decimal point!
Multiplying two decimal numbers is the same as multiplying two whole numbers with the exception that we need to take care of the decimal point.
Let’s learn this with the help of an example.
Let’s multiply 1.5 and 1.2.
Step 1: Count the number of digits after the decimal point in both the numbers.
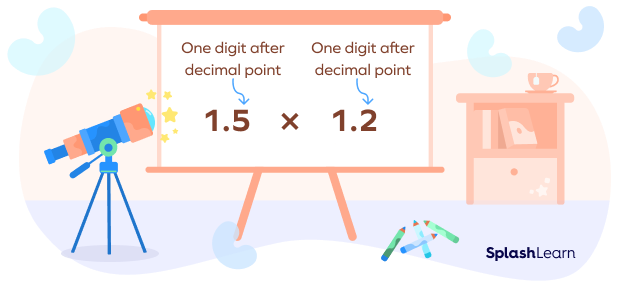
Step 2: So the total number of digits after the decimal point in our multiplication expression is 1 + 1 = 2.
Step 3: Multiply the two numbers without the decimal point.

Step 4: In this product, start from the right and place the decimal point, after the same number of places as the total number found in step 2. And that will be the answer to our decimal multiplication.

So the product of 1.5 and 1.2 will be 1.80.
Solved Examples
Example 1: Jake has 4 boxes of apples. If 1 box has 3 apples, how many apples does he have?
Solution: In this example, the multiplicand is 3 and the multiplier is 4.
Hence, the total number of apples Jake has = the product of 4 and 3.
or 4 ✕ 3 = 12
Example 2: Calculate the product of $\frac{3}{7}$ and $\frac{5}{6}$.
Solution: $\frac{3}{7} ✕ \frac{5}{6} = \frac{3 ✕ 5}{7 ✕ 6} = \frac{15}{42}$
Example 3: Calculate the product of 125 and 34 .
Solution: First, let’s convert the mixed number into fraction form.
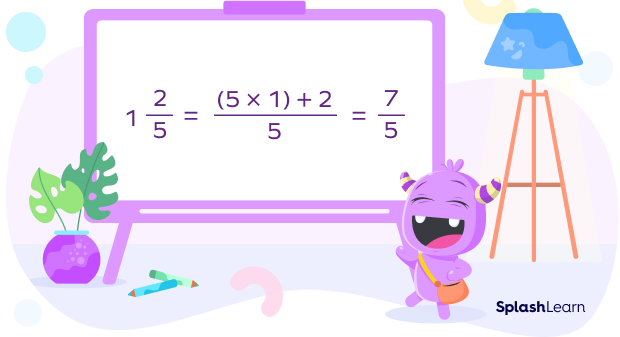
So, multiplying $1\frac{2}{5}$ and $\frac{3}{4}$ is the same as multiplying $\frac{7}{5}$ and $\frac{3}{4}$ .
Following the steps of fraction multiplication, we get,
$\frac{7}{5} ✕ \frac{3}{4} = \frac{7 ✕ 3}{5 ✕ 4} = \frac{21}{20} = 1\frac{1}{20}$.
Example 4: Calculate the product of 0.09 and 0.3.
Solution.: First, let’s count the number of decimal places.
Number of decimal places in 0.09 = 2
Number of decimal places in 0.3 = 1
The total number of decimals places in the final answer = 2 + 1 = 3
Now let’s multiply the two numbers without the decimal point: 9 ✕ 3 = 27
Placing the decimal point from the right after 3 digits in this product, we get 0.027.
Therefore, 0.09 ✕ 0.3 = 0.027.
Practice Problems
Product in Math - Definition With Examples
Judy has 4 boxes with 6 cookies each. How many cookies does she have in total?
Here, the product will be number of groups ✕ number of objects in each group
4 ✕ 6 = 24
Calculate the product of $\frac{7}{2}$ and $\frac{4}{3}$ .
$\frac{7}{2} ✕ \frac{4}{3} = \frac{7 ✕ 2}{4 ✕ 3} = \frac{14}{12} = \frac{12}{12}$.
Calculate the product of 0.5 and 0.3
Total number of decimals places = 1 + 1 = 2
Product without decimal point, 5 ✕ 3 = 15
Therefore, 0.5 ✕ 0.3 = 0.15.
Jimmy has 4 bags with 3 candies each, and Joe has 3 bags with 4 candies each. Who has more candies?
Number of candies with Jimmy = 4 ✕ 3 = 12
Number of candies with Joe = 3 ✕ 4 = 12
Thus, both have an equal number of candies.
Frequently Asked Questions
What happens when you calculate the product of a number and 0?
When you calculate the product of a number with 0, you get the answer as 0.
For instance, 5 ✕ 0 = 0; this is called the zero property of multiplication.
What is a multiplicand and a multiplier?
A multiplicand represents the number of equal groups, and a multiplier represents the number of objects in each group. For instance, consider the following equation:
2 ✕ 7 = 14
Here, 2 is the multiplicand, 4 is the multiplier, and 14 is the product.
What is the identity property of multiplication?
It states that any number multiplied by 1 gives the same result as the number itself. For instance, 35✕ 1 = 35.




































