What Are Base-Ten Numerals?
The base of a number system tells us how many unique digits are used to form a number in that system. In the base ten system, ten unique digits (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are used to represent any number. Number is an arithmetic value that we use for the purpose of counting.
The ten digits used in the base 10 number system to form the base ten numerals are as follows:
Recommended Games
Base Ten Numerals Definition
Base ten numerals are written with a combination of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, such that each position has a value in powers of ten.
Base Ten Numerals Example: 150 and “One hundred and fifty” are both base ten numerals. The first is written using the digits. The latter is written in the word form.
Recommended Worksheets
Base-Ten Place Value Chart
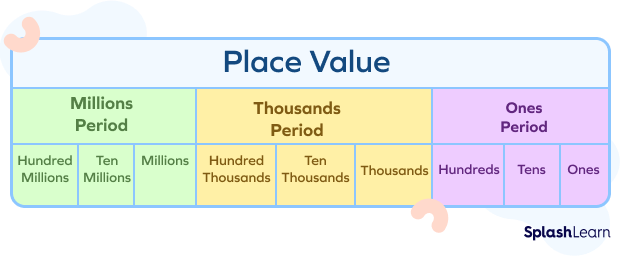
The place value of a digit tells us about the value of that digit, based on the position of the digit in the number. A place value table or chart helps to name each place value. The different groups of place values are called periods. Periods help us to determine the place values easily. The place value table is given below:
Consider the base ten numeral 5,219,037.
On placing the number on the place value table, we get
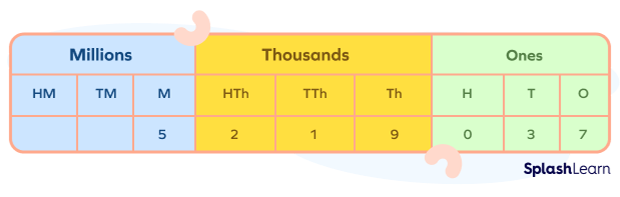
We read it using the place value chart as “Five million two hundred nineteen thousand thirty-seven.”
How to Find the Place Value of a Digit?
Let’s find the place value of all the digits in 345,162 using the following steps.
- Step 1: Place the digits in the place value chart. In this case, we get:
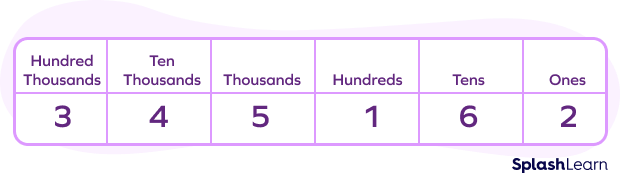
- Step 2: Find the place where each digit is located.
- Step 3: Multiply the digit by its matching place value.
Place Value of 2 is $2 \times 1 = 2$
Place Value of 6 is $6 \times 10 = 60$
Place Value of 1 is $1 \times 100 = 100$
Place Value of 5 is $5 \times 1000 = 5000$
Place Value of 4 is $4 \times 10000 = 40000$
Place Value of 3 is $3 \times 100000 = 300000$
Expanded Form
Expanded form of a number is a way of expressing the number using its place values.
Example:
- Write the expanded form of 531,264.
Place value of $4 = 4$
Place value of $6 = 6 \times 10 = 60$
Place value of $2 = 2 \times 100 = 200$
Place value of $1 = 1 \times 1000 = 1000$
Place value of $3 = 3 \times 10000 = 30000$
Place value of $5 = 5 \times 100000 = 500000$
Expanded form of $531,264 = 500000 + 30000 + 1000 + 200 + 6 $
- The number 4531 can be written in expanded form as
$4531 = 4000 + 500 + 30 + 1$
- Expanded form of 2836
$2836 = (2 \times 1000) + (8 \times 100) + (3 \times 10) + (6 \times 1)$
$= 2000 + 800 + 30 + 6$
Place Values in Decimals
Decimal numbers are the numerals whose whole part and fractional part is separated by a decimal point.
Example 1: Consider the decimal 125.473
The place value chart shows the place values of the different digits in a decimal.
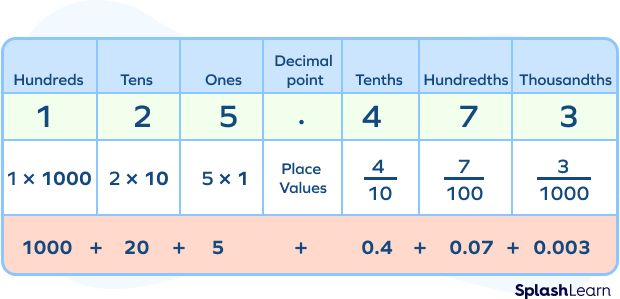
Example 2: Suppose we have a decimal number 345.27.
Place value of 7 will be $7 \times \frac{1}{100} = \frac{7}{100}$
Place value of 2 will be $2 \times \frac{1}{10} = \frac{2}{10}$
Place value of 5 will be $5 \times 1 = 5$
Place value of 7 will be $4 \times 10 = 40$
Place value of 7 will be $3 \times 100 = 300$
Expanded form of $345.27 = 300 + 40 + 5 + \frac{2}{10} + \frac{7}{100}$
$= 3 \times 100 + 4 \times 10 + 5 \times 1 + 2 \times \frac{1}{10} + 7 \times \frac{1}{100}$
$= 3 \text{hundred} + 4 \text{tens} + 5 \text{ones} + 2 \text{tenths} + 7 \text{hundredths}$
Fun Fact!
Base ten numerals form the basis for our counting system and thus, our monetary system. We use them in our daily lives for counting, measurements, and calculations.
Let’s Do It!
Instead of handing out place value worksheets to your child, ask them to use base ten blocks to show the place value. This will help them to not only help them to understand how base ten numerals are written, but also their place value.
Conclusion
In this article, we learned about the base ten numeral form. Base ten numeral form is the expansion of a number using the place value. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. Write 4326.18 in its expanded form.
Solution:
$4326.18 = (4 \times 1000) + (3 \times 100) + (2 \times 10) + (6 \times 1) + (1 \times \frac{1}{10}) + (8 \times \frac{1}{100})$
$4326.189 = 4000 + 300 + 20 + 6 + 0.1 + 0.08$
2. What is the place value of 6 in 75683?
Solution:
In the given base ten numeral, the digit 6 lies at hundreds place.
The place value of 6 in $75683 = 6 \times 100 = 600$
3. Give the place values of the digits 2 and 5 in the number 75.1824
Solution:
Place value of 2 in $75.1824 = 2 \times 0.001 = 0.002$
Place Value of 5 in $75.1824 = 5 \times 1 = 5$
4. Write the place values of the digit 9 in the number 948.319?
Solution:
| Hundreds | Tens | Ones | DecimalPoint | Tenths | Hundredths | Thousandths |
| 9 | 4 | 8 | . | 3 | 1 | 9 |
Place value of the digit 9 at hundreds place$ = 9 \times 100 = 900$
Place value of the digit 9 at thousandths place $= 9 \times 10000 = 90000$
5. Write the base ten numeral for the given expanded form.
$4 \times 10000 + 5 \times 1000 + 7 \times 100 + 9 \times 10 + 2 \times 1 =$ ?
Solution:
$4 \times 10000 + 5 \times 1000 + 7 \times 100 + 9 \times 10 + 2 \times 1$
$= 40000 + 5000 + 700 + 90 + 2$
$= 45792$
Practice Problems
Base-Ten Numeral - Definition with Examples
Which of the following is the correct expanded form for 432.987?
The correct base ten numeral form for $432.987 = 400 + 30 + 2 + 0.9 + 0.08 + 0.007$
What is the place value of 0 in 7082?
0 lies in the hundreds place.
Place value of $0 = 0 \times 100 = 0$
Find the difference between the place value of 2 in 652.729.
Place value of $2 = 2$ and $0.02$
Difference $= 2$ $–$ $0.02 = 1.98$
Write the base ten numeral. 4 hundreds $+ 2$ tens $+ 5$ ones $+ 6$ tenths $+ 7$ hundredths $+ 1$ thousandths
4 hundreds $+ 2$ tens $+ 5$ ones $+ 6$ tenths $+ 7$ hundredths $+ 1$ thousandths
$= 400 + 20 + 5 + 0.6 + 0.07 + 0.001$
$= 425.671$
What’s the base ten numeral represented by $9000 + 600 + 40 + 8$?
$9000 + 600 + 40 + 8 = 9684$
Frequently Asked Questions
What is the binary number system?
The binary number system is simply the base-2 number system that uses only 2 digits (0 and 1) to form all the numbers.
What is the base ten block in math?
Base ten blocks are simply the visual representation of base ten place values that represent different place values (ones, tens, hundreds, etc) using blocks.
What is another name for the base-ten system?
The base ten system is also known as the decimal number system since the place values of digits are determined based on their position with reference to the decimal point.
Do all numbers use the base ten system?
Yes! Almost all countries across the world use the base ten number system.




































