Decompose means to separate or break apart. We can decompose numbers as well as geometric shapes.
Suppose you have just one sandwich made from two square-shaped bread slices, and you want to share it with your friend. What will you do?
You can split the sandwich into two halves so that each one of you can enjoy it equally. So, now you will both have two triangle-shaped sandwiches. This means that you took a square shape and split it into two triangles. In other words, you decomposed the square to make two triangles.
Does that sound interesting? Come on then, let’s learn more about decomposition.
What Is Decomposing Numbers?
It means to break apart numbers into two or more parts. All numbers can be split or broken down.
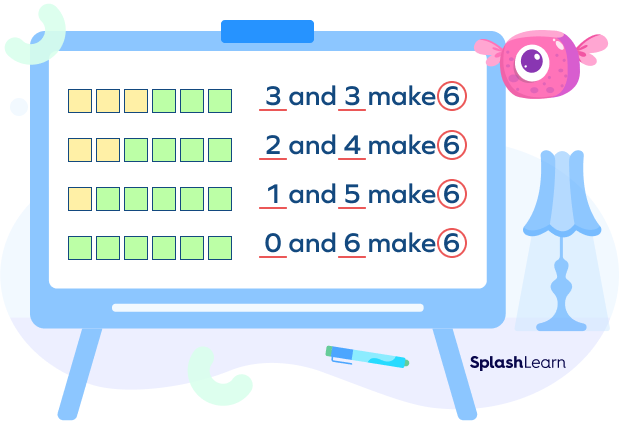
For example, consider the number 6. Think of the different ways in which you may separate 6 into parts.
- 3 and 3
- 2 and 4
- 1 and 5
- 0 and 6
These parts are the decomposed numbers of 6.
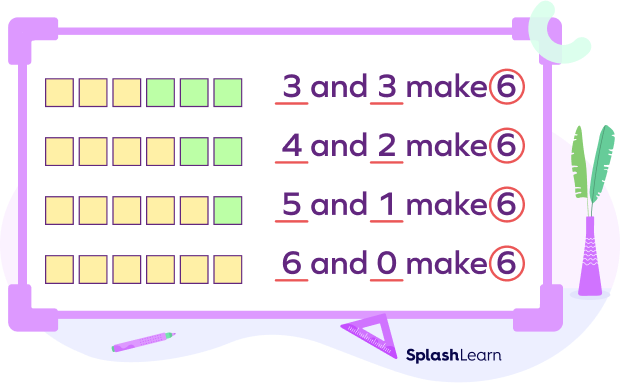
You can even reverse the order of the parts as well, such as:
- 3 and 3
- 4 and 2
- 5 and 1
- 6 and 0
Recommended Games
How to Decompose Numbers?
Numbers can be decomposed in two ways: place value method and the addend method.
Decomposing a Number Using Place Value Method
In this method, you separate a number into its tens and ones.
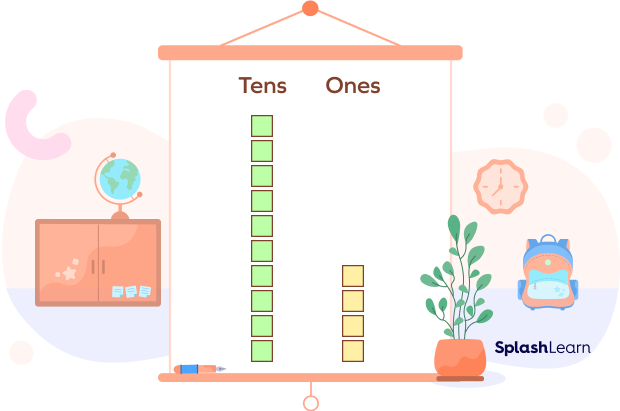
Example: Consider the number 14. It has two digits, 1 and 4. The digit 1 is in the tens place, and the digit 4 is in the ones place. This means 14 has 1 ten and 4 ones. You can write 14 as:
14 = 10 + 4 (1 ten + 4 ones)
So, 14 can be decomposed as 10 + 4.
Let us consider another example, 19. Here, digit 1 is in the tens place, and digit 9 is in the ones place. This means 19 has 1 ten and 9 ones. You can write 19 as:
19 = 10 + 9 (1 ten + 9 ones)
So, 19 can be decomposed as 10 + 9.
Decomposing a Number Using the Addends Method
In this method, you separate a number into its different addends.
Note: Addend refers to the numbers you add to form the sum. For example, 2 + 1 = 3. Here, 2 and 1 are addends.
Example: Consider the number 9. To decompose 9 into its addends, you will have to think of how you can create this number using smaller numbers.
- 9 = 0 + 9
- 9 = 1 + 8
- 9 = 2 + 7
- 9 = 3 + 6
- 9 = 4 + 5
Recommended Worksheets
What Does It Mean to Decompose Shapes?
To decompose shapes means to break shapes into two or more shapes. The smaller shapes may resemble the larger shape or may be entirely new shapes.
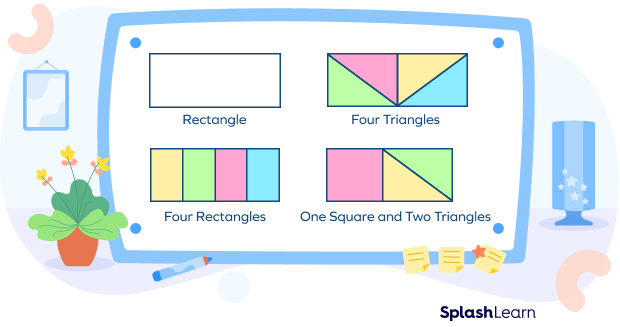
For example, let us take a rectangle. We can break it into several shapes. We can break it down to form smaller rectangles, triangles, a combination of squares and triangles, a combination of rectangles and triangles, etc.
Figure 4 shows some of the shapes we can get by decomposing a rectangle.
Decomposing Shapes in Real Life
Decomposition in Math is evident in day-to-day life. Some examples of decomposing shapes in real-life are:
- Cutting a pizza into slices. Here, we break apart a circular figure into several sectors.
- Tearing an A4 sheet of paper into two halves. Here, we split a rectangle into two smaller rectangles.
- Cutting a slice of lemon in half. Here, we slice a circle into two semicircles.
Process of Decomposing Shapes
There are no fixed rules to follow when it comes to decomposing shapes. You have to think about breaking up a shape to form smaller standard geometric shapes.
Consider figure 5 below, which depicts a rocket. When you think of it as a rocket, you will visualize a single figure. But when you think of it in terms of shapes, you will identify various geometric shapes. You can separate this figure into several smaller shapes, such as triangles, trapezoids, squares, and rectangles.
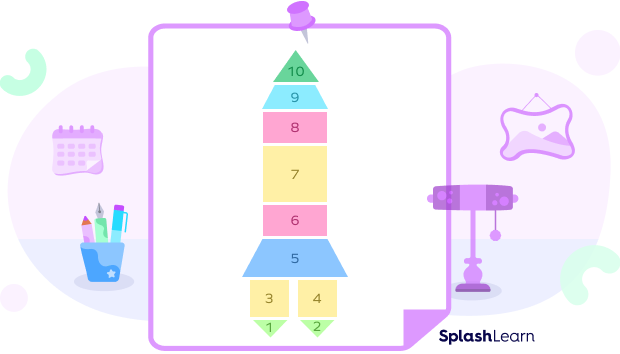
Fig. 5: Figure depicting a rocket. Here, sections 1, 2, and 10 denote triangles; 3, 4, and 7 denote squares; 5 and 9 denote trapezoids; and sections 6 and 8 denote rectangles.
Conclusion
Decomposition in Math is an essential skill for understanding higher concepts of math and geometry. Decomposing numbers helps to develop number sense and relationships between digits. Decomposing shapes sets the stage for understanding the concepts of perimeter, area, and volume.
Solved Examples
Example 1: Decompose the number 10.
Solution: For decomposing 10, we separate it into its addends.
10 = 1 + 9
10 = 2 + 8
10 = 3 + 7
10 = 4 + 6
10 = 5 + 5
Example 2: Decompose the number 12.
Solution: in the number 12, the digit 1 is in the tens place, and the digit 2 is in the ones place. So, decomposing 12 into tens and ones will be equal to:
12 = 10 + 2 (1 ten + 2 ones)
Example 3: Can you decompose the given hexagon into three rhombuses?
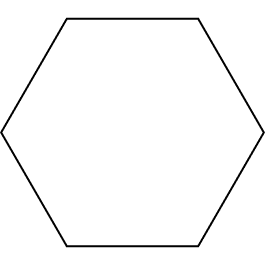
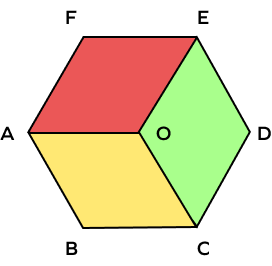
Solution: Yes, it is possible to decompose the given hexagon into three rhombuses.
Let us consider O to be the center of the rhombus. We draw three line segments connecting the center to the three alternate vertices of the hexagon, A, E, and C. This will give us three rhombuses, AOEF, AOCB, and DEOC.
The figure below illustrates this decomposition.
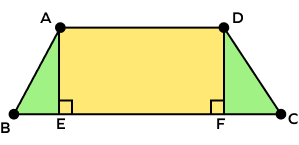
Example 4: How can we decompose the given trapezoid into two triangles and a rectangle?

Solution: We first draw two line segments, AE and DF, so that they meet the side BC at right angles. This will give us the rectangle AEFD and the two triangles ABE and DCF.
The figure below illustrates this decomposition.
Practice Problems
Decomposing Numbers in Math – Definition, Methods & Examples
If you decompose the given triangle into two shapes, which of the following pairs of shapes can you get?
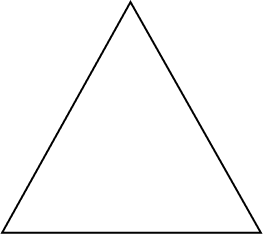
In a triangle, there are no curved edges or right angles. So, we can’t break it into a circle or a rectangle. But if we draw a line
segment DE that runs parallel to the base BC of the triangle, we will get a triangle ADE and a trapezoid DBCE.
Which of the following congruent shapes can you get from a rectangle if you decompose it?

If we connect the opposite vertices of a rectangle with a line segment, we get two congruent triangles, as shown in figure (a) below.
If we draw a line segment to connect the midpoints of the opposite sides of a rectangle (that are shorter), we get two congruent rectangles, as shown in figure (b) below.
If we divide a rectangle into half and repeat the above steps, we get two congruent rectangles and triangles. Figure (c) below illustrates this decomposition.
Which of the following can you get if you decompose 8?
If we add 6 + 2, we get 8. But we don’t get 8 on adding 4 and 3 or 4 and 1. So, we can break 8 as 6 + 2.
Which of the following can you get if you decompose 15 into tens and ones?
Here, digit 1 is in the tens place, and digit 5 is in the ones place. So, we can split 15 as 10 + 5 (1 ten and 5 ones).
Frequently Asked Questions
When we decompose a figure, can we get a shape that is congruent to the original shape?
No, when we decompose a figure, we can’t get a shape that is congruent to the original shape. This is because congruent shapes are of equal sizes, and decomposing means breaking down a shape into smaller shapes.
What is the difference between decomposing and composing shapes?
Decomposing shapes means breaking them into smaller shapes while composing shapes means building a new or larger shape using smaller shapes.
What is the difference between composing and decomposing numbers?
Composing numbers means adding two or more numbers to create a larger number. Decomposing numbers means breaking a number into smaller numbers.




































