Estimate – Definition with Examples

What Is Estimation?

Estimating is not something new to us. We do it all the time. Look at the image given below. We can see that Eddie, in the image below, is not exactly 2 feet tall but he is close to it. So, we can estimate his height and say that he is about 2 feet tall. 

A few more such examples:

Estimating time: Sara walks to school from home in about 10 minutes. 

Estimating quantity: About a 1000 people will attend the concert.

Estimating distance: The distance between New York to San Francisco is approximately 2900 miles.

So, the question is, what is an estimate? 

An estimate is an approximate calculation or rounding of the number to the nearest place value for the sake of convenience. There’s no single way to define estimation. The closest meaning of an estimation is a guess or an assumption about a value that isn’t too far off. What is an estimate in Math? Definition for estimate in math is an approximate value close enough to the correct value. A lot of guesses are made to make math easier and clearer. 

Definition of Estimation

Estimation is a rough calculation of the actual value, number, or quantity for making calculations easier. 

Example: When taking a cab or waiting for a bill at a restaurant, we tend to estimate the amount to be paid.

In short, it is an approximate answer. And this figure is often used to check the accuracy or correctness of the final answer. Estimation helps when a certain margin of error is allowed in a calculation. It gives an answer without using a calculator or written calculations. The whole point of the exercise is for you to devise a plausible approximation.

Most of the time, estimation in math is done by rounding off the numbers to their closest whole value to get a quick and simple rough answer. It saves time and effort.

For instance, kids use estimation many times a day without realizing it. They tend to figure out how long they play and how long they have for recess. 

Examples of Estimation

• Lily counted the number of flowers in the garden by counting the first row and then multiplying it by the number of rows. She estimated that there were 300 flowers in the garden. 

• Anna made exactly $\$9.7$ from her lemonade stand. When asked by her parents, she estimated that she made about $\$10$ from the stand. 

• The total population in the world as of April 2022 is around 7.9 billion. This is an estimation. This is not the exact value. 

Non-examples of Estimation

• There are eight planets in the solar system. 
• There are 50 states in the United States. 

There is no estimation in both of these examples. They are facts. 

Estimate Symbol Math

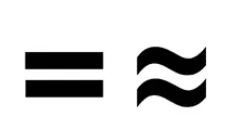
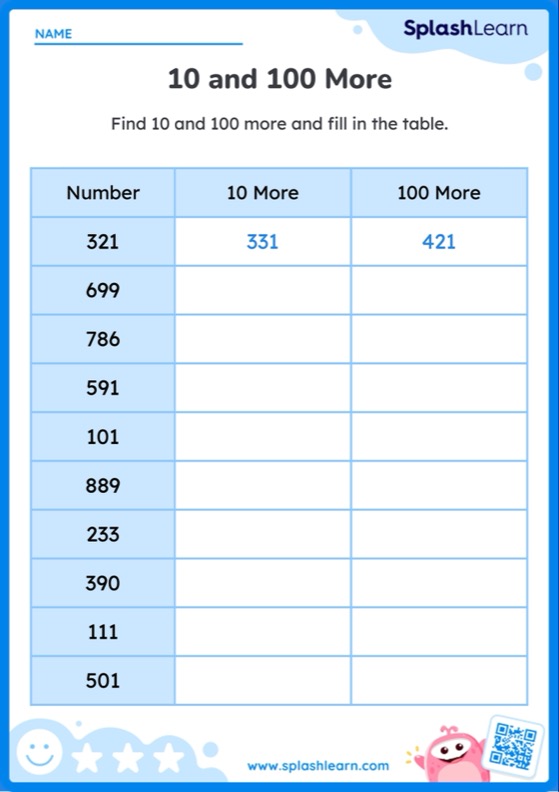
We use the first symbol “$=$” sign when things are exactly the same but if we estimate then we make an approximate guess hence we use the second symbol “$\approx$ “ which means ‘approximately equal to’.

How to Estimate in Math?

An important method of estimating numbers in math is to skillfully round off the numbers. What is rounding of numbers? Rounding a number refers to changing or altering the number to a less exact but more convenient number, making it simpler for calculations. The estimated answer is easier to use. Rounding off comes in handy while finding solutions to estimation questions.

Let us consider an example of estimation: The headmistress of a school estimates that about 24 students are standing in rows in the playground. She does this by counting the number of students in a single row and then multiplying that figure by the total number of rows. The actual number may be more than or less than 24.

The General Rules in Estimating

First, we must know the digit in the place we want to round the number off to. Next, we check the number to its right. Example: To round off to the nearest ten, we check the ones place.

1) If the number is less than 5, we round it down. 

For example, 723 rounded off to the nearest ten is 720. 

          We drop 3 since $3 \lt 5$. We do not change the tens digit.

2) If the number is more than or equal to 5, we round it up. 

For example, 787 rounded off to the nearest ten is 780. 

           We round the tens digit 8 up to 9 since $7 \gt 5$.

How to Estimate Different Place Values?

The simplest way to estimate is by rounding off numbers to the nearest whole number.  Rounding off helps achieve an approximate answer faster. For example, Laura pays a monthly installment of $\$3950$ for her new house. We can round off this number to $\$4000$ to simplify.

You can round off a number to the nearest 10, 100, or 1000 and so on. 

When working on problems involving large numbers, we may have to estimate our answers to the closest million or billion. Let us understand this better with the estimated digit examples. 

Example: Let’s round off the number 381.93 to three different place values.

1. Round it to a whole number:

It means we wish to lose the decimal part. The tenth place is 9, which is greater than 5. So, we round it up. Let us increase the digit in one’s place by 1. We will get 382.

2. Round to the nearest ten: 

To round a number to the nearest ten, we check the ones place. Here, it is 1. We round it down, since $1 \lt 5$. We will simply drop 1. The rounded number is 380.

3. Round it to the nearest hundred: 

The tens place is 8. We round it up and increase the digit in the hundreds place by 1. The rounded number is 400.

4. Round it to the nearest tenth:

The hundredths place is 3 and $3 \lt 5$. So, we drop 3 and round the decimal to 381.9.

General Rule of Estimation Summary:

• As soon as you pick the number you want to estimate/round, first find the digit at the place you want to round the number to.
• Next look at the digit right to that place to see which way you will round. 
• If the digit to the right is four or less (as in 4, 3, 2, 1, 0), your number remains the same. 
• If the digit to the right is five or higher (as in 5, 6, 7, 8, or nine), your number increases by one. 
• In the end, all the extra digits that weren’t rounded off, should be removed. 

A quick way to remember this rule is:

Estimation in Real Life

Estimating is a vital part of our daily lives. We are always estimating things, sometimes without even being aware of it.

Example 1:

When we are purchasing a few things at the supermarket, we try to estimate the total cost in our head. The estimated amount is usually a round number in tens, hundreds, or even thousands, depending on what items we wish to purchase.

Suppose you buy three items whose prices are $\$2.35$,  $\$13.85$ and $\$4.25$. To estimate the total cost, you can simply round the price to the nearest whole number.

Example 2: Dividing $\$798$ bill among 8 people.

Rounding off 798 to the nearest ten, we get 800.

$800 \div 8 = 100$

So, the estimate of the share of each person is $\$100$.

Example 3: Estimate the product of 62 and 29. We round off to the nearest ten. We change 62 to 60, and 29 to 30. 

Estimate Using Compatible Numbers

When we use estimation to approximate a calculation, we can replace actual numbers with compatible numbers (friendly numbers). Compatible numbers are numbers that are easy to add, subtract, multiply, and divide.

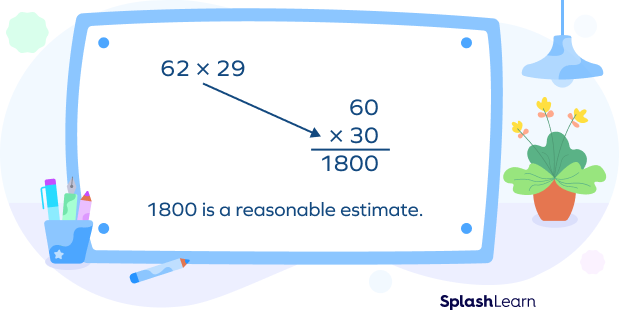
Example: Multiply 14 and 68 using compatible numbers.

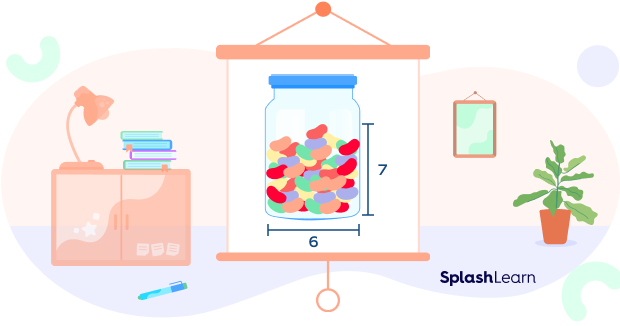
Estimation Jar: How Does It Work?

An estimation jar is a delightful and engaging teaching aid. It is widely used to introduce the concept of estimation to kids. 

Children love making predictions. The jar can be filled with fun items children enjoy, like rubber ducks, marshmallows, Cheerios, beads, or jelly beans. Kids are usually asked to estimate the number of candies in the jar. 

An approximate method to calculate the number of sweets in a jar is to multiply the approximate number along the base by the approximate number of sweets along the height of the jar.

We can say that there are approximately $7 \times 6 = 42$ candies in the given jar.

Conclusion

You have learned that there is much more to estimation than guesswork. It is a concept that helps you gauge, analyze and come up with solutions. It encourages you to think out of the box.

It also improves your attention to detail and makes you a better negotiator. Now that you have all the skills required to be an expert at estimating, I estimate that you are about to have a good time with it.

Solved Examples

1. Round 412.74 to the nearest tenth.

Solution:

Hundredths digit $= 4 \lt 5$

Thus, we drop 4.

Rounding 412.74 to the nearest tenth, we get 412.7.

2. Round off the number 525.71 to the nearest whole number.

Solution:

The tenth place of the number 525.71 is 7. So, we round it up. Let us increase the digit in ones place by 1. We will get 526.

3. A parking garage has 4 levels. If each level can house 105 cars, estimate the number of cars parked there.

Solution:

Let us multiply the number of levels with the rounded number of cars.

$4 \times 100 = 400$

So, the estimated number of cars parked in the garage is 400.

4. Aaliyah has 47 baseball cards, and Harry has 62. Estimate how many cards they have altogether.

Solution:

Let us round off the number of baseball cards Aaliyah and Harry have. Let’s round the numbers to the nearest ten. 47 is rounded to 50, and 62 is rounded to 60.

Therefore the total number of cards they have altogether is $50 + 60 = 110$ baseball cards (approximately)

5. Estimate the difference of 14.21 and 5.67.

Solution:

Let us round off the numbers.

14.21, rounded to the nearest whole number, is 14.

5.67 is rounded to 6.

By subtracting we get $14 – 6 = 8$

The estimated difference is 8.

6. Aaron scored 87.91% in his seventh grade Science finals. Round off his percentage to the nearest whole number. 

Solution: Aaron scored approximately 88% in seventh grade Science finals. This estimation was made after rounding off the number 87.91% to the nearest whole number. Since the number to the right after the decimal is 9 which is greater than 5, the number to the left(7) increases by one digit. 

7. Gina collected 56 coins and Carol collected 86 coins. Choose a better estimate to find the number of coins they own together. 

Solution: Gina collected 56 coins. We can round off 56 to 60 coins and we can round off 86 to 90 coins. After adding 60 and 90, we get 150. The estimated answer is 150. 

8. Sam wants to buy 5 books, each costs $\$2.95$. The bundle of the 5 books together costs $\$20$. Is that correct?

Solution:No, that doesn’t seem correct.

Each book costs approximately $\$3$. Five such books should cost $5 \times \$3 = \$15$. 

$\$20$ seems too much.

Practice Problems

Frequently Asked Questions