What is Zero – Definition with Examples

Zero – Introduction

Have you ever wondered what the definition of zero is in math?

Zero is the number that represents no amount or no objects. The numbers 1, 2, 3, and onwards are called natural numbers. Zero and the natural numbers together are called whole numbers. Zero is represented by the symbol “0.”

If you’re wondering what is zero in math, you might also be wondering, is zero a real number in math?

Yes! Zero is a real number because it is an integer. Integers include all negative numbers, positive numbers, and zero. Real numbers include integers as well as fractions and decimals.

Zero also represents the absence of any negative or positive amount. For example, if you have 3 oranges and add zero oranges to that, you still have 3 oranges.

Another name for zero in math is thus “null,” as it represents the absence of any number.

Alt tag: Null representation using an example

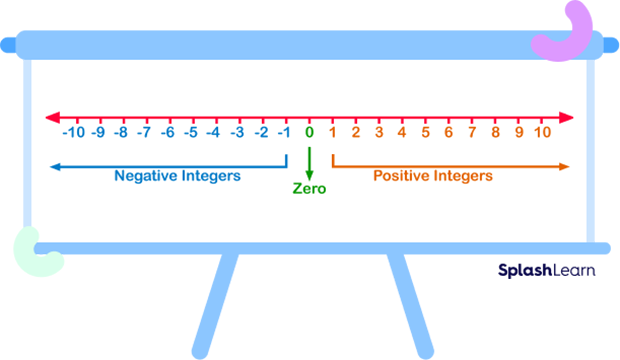
Position of Zero on the Number Line

Zero occurs between $-1$ and 1. It is the integer that separates negative numbers from positive numbers. Zero itself is neither negative nor positive. Don’t you think that’s fascinating?

Alt tag: Position of zero (0) on the number line

History of Zero

• The Mayans used zero between numbers to express time periods and denote the dates of the calendar.
• The Indians were the first to use zero like any number and gave the zero meaning in math. For this reason, the concept of zero in math is considered to have originated in India. 
• The Arabians adopted zero as a number to represent emptiness as well as infinity.

What Are the Properties of Zero?

Zero also has certain special properties that make it unique. These properties help define what zero is in math.

Each property of zero tells us how it interacts with other numbers through operations like addition, subtraction, division, or multiplication. Let’s understand how these properties work in operations with zero!

Different Arithmetic Operations with Zero

Operations with zero can be understood based on its addition property, subtraction property, multiplication property, and division property. Let’s take a look at these:

Addition Property

• When zero is added to another number, the sum will be the number itself.

$a + 0 = a$

For example: $5 + 0 = 5$

Subtraction Property

• When zero is subtracted from another number, the difference will be the number itself.

$a – 0 = a$

For example, $8$ $-$ $0 = 8$. 

• When a number is subtracted from itself, the result will also be zero.

$a$ $-$ $a = 0$

For example, $4$ $-$ $4 = 0$. 

Multiplication Property

• When zero is multiplied by another number, the product will always be zero.

$0 \times a = 0$

For example, $0 \times 6 = 0$

Division Property

• If zero is divided by another number, the quotient is zero.

For example, $0/11 = 0$

• However, if a number is divided by 0, the result is undefined.

Imagine trying to divide 12 oranges into zero groups—it’s not possible! There has to be at least one group.

For this reason, when a number is divided by 0, the result is considered to be undefined in math.

The Use of Zero as a Placeholder

Alt tag: Using zero as a placeholder

Zero plays an important role as a placeholder in numbers.

For example, in 502, 0 marks the tens place. If not for the 0, the number would be 52, or it would have to be written as 5 2. This would be confusing because it would not be clear if it represents 502, 5002, or 500002. This is why 0 is used as a numerical digit.

How Many Zeros Are In 1 Million?

There are six zeros in 1 million. Without all those zeros, 1 million would be 1. You can thus see the importance of zero in math!

Place Value Of Zero In Decimals

• In a decimal number, the zero or zeros between other digits are important because they act as placeholders.

For example, in 4.055, the zero is a placeholder.

In 3.502 as well, zero is a placeholder. 

• However, the zero or zeros to the right of the decimal number after the decimal points does not impact the value of the number.

For example, in 5.60, zero does not impact the value of the number and is the same as 5.600.

Conclusion

Zero is an important number, even though it represents a quantity of nothing!

To summarize: Zero is a number between negative numbers and positive numbers. It is necessary as a placeholder in whole numbers and decimal numbers. It represents a place with no amount or null value.

The properties of zero are unique. No other number behaves the way zero does in math operations. These properties of zero help us understand what zero is in math.

Solved Examples

1. If one of the digits in a 3-digit number is 0, where should it be placed (at hundreds, tens or ones) to make the smallest 3-digit number.

Solution: The position of 0 has to be in the tens place.

2. Calculate the following: $66$ $-$ $66 + 9$ $-$ $0 =$ ?

Solution: When a number is subtracted from itself, the resulting number is zero.

Therefore, $66$ $-$ $66 = 0$

When a number is added to zero, the sum is the number itself.

Therefore, $0 + 9 = 9$

If you subtract zero from a number, you get that number itself.

Therefore, $9$ $-$ $0 = 9$

So, $66$ $-$ $66 + 9$ $-$ $0 = 9$

3. Calculate the following: $7 \times 10 \times 0 \times 65 =$ ?

Solution: When we multiply a number by 0, the resulting number is 0 itself. Similarly, when zero is multiplied by a number, the product is 0. 

Therefore, $7 \times 10 \times 0 = 0$ 

$0 \times 65 = 0$ 

So, $7 \times 10 \times 0 \times 65 = 0$

4. Solve the following: $25/0 =$ ? 

Solution: A number cannot be divided by 0 as it is not logically possible. So the result is considered to be undefined. Therefore, $25/0 =$ Undefined

5. Solve the following: $0 / 34 =$ ?

Solution: When 0 is divided by a number, the resulting number is 0.

So, $0/34 = 0$.

Practice Problems

Frequently Asked Questions