Octagon Formula For Area and Perimeter With Derivation

What Are The Octagon Formulas?

The octagon is an 8-sided polygon. An octagon is referred to as a regular octagon if all of its sides have equal lengths and angles are of equal measures. A regular octagon has each interior angle measuring $135^{\circ}$ and each exterior angle measures $45^{\circ}$. 

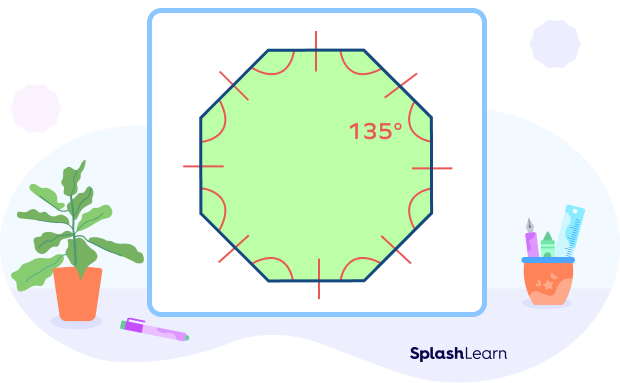
We will discuss octagon formulas such as the area of an octagon, perimeter of an octagon.

The Formula for the Area of an Octagon

Area of an octagon is the region bounded within the boundaries of an octagon. The area of an octagon $= 2a^{2}(\sqrt{2} + 1)$

where a represents the side of the octagon.

Derivation

To find the area of an octagon, it is divided into 8 equal isosceles triangles. The entire area of the polygon can be determined by multiplying the area of one triangle by 8. 

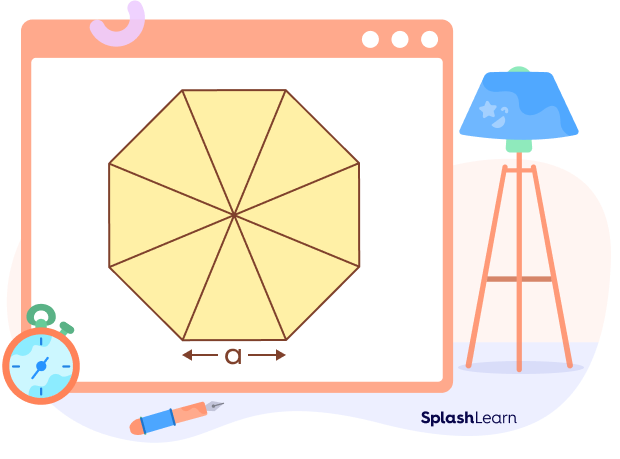
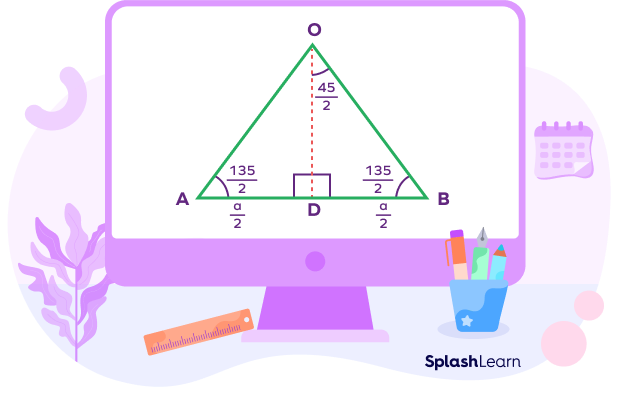
One isosceles triangle is shown below where $OA = OB$. 

Here, OD is the height of the triangle, and AB is the base of the triangle. Let OD bisects the angle AOB and the side AB.

Here, base $= AB = a$

Area of octagon $= 8 \times\; Area\; of\; one\; isosceles\; triangle$

By using the identities, we have

$tan^{2}(\frac{\theta}{2}) = \frac{1 \;-\; cos\; \theta}{1 \;+\; cos\;\theta} = \frac{1\;-\; cos\; 45^{\circ}}{1\;+ \;cos\; 45^{\circ}} = \frac{1-(1\sqrt{2})}{1+(1\sqrt{2})} = \frac{\sqrt{2}\;-\;1}{\sqrt{2}\;+\;1} = (\sqrt{2}\;-\;1)^{2}$

$tan\; (\frac{45^{\circ}}{2}) = \frac{BD}{OD} = \sqrt{2}\;-\;1$

Thus, $OD = \frac{BD}{\sqrt{2}\;-\;1} = \frac{a/2}{\sqrt{2}\;-\;1} = \frac{a(\sqrt{2}\;+\;1)}{2}$

Area of $\Delta AOB\; = 12 \times AB \times OD$

$= \frac{1}{2} \times a \times \frac{a}{2}(\sqrt{2}\;+\;1)$

$= \frac{1}{4}a^{2}\;(\sqrt{2}\;+\;1)$

Area of octagon $= 8 \times$ Area of one isosceles triangle

Area of octagon $= 8 \times \frac{1}{4}a^{2}\;(\sqrt{2}\;+\;1)$

Area of octagon $= 2a^{2}\;(\sqrt{2}\;+\;1)$

Formula of the Perimeter of Octagon

The length of an octagon’s boundary is referred to as its perimeter. Therefore, the perimeter will equal the total length of all sides. The formula for the perimeter of a regular octagon having 8 sides each measuring “a” units is given by

So, the perimeter of a regular octagon = 8a units

Octagon Formulas

Area of a regular octagon $= 2s^{2}\;(1\;+\;\sqrt{2})$

Perimeter of a regular octagon $= 8s$

Properties of a Regular Octagon

• There are 8 sides and 8 interior angles.
• A regular octagon has a total of 20 diagonals.
• Each inside angle measures $135^{\circ}$. The sum of interior angles is $1080^{\circ}$.
• Each exterior angle measures $45^{\circ}$, so the sum of all the exterior angles is $360^{\circ}$.

Conclusion

In this article, we learned about octagon, octagonal formulas, derivation of octagon formula, and properties of a regular octagon.  Let’s solve a few examples now.

Solved Examples based on Octagon Formulas

1. If the length of an octagon’s side is 14 inches, calculate its area.

Solution:

The side’s length, “s,” is 14 inches.

Using the octagon’s surface area formula,

$A = 2s^{2}\;(\sqrt{2}\;+\;1)$

$A = 2 \times14^{2}\;(\sqrt{2}\;+\;1)$

$A = 946.37$ square inches

As a result, the octagon has a surface area of 946.37 square inches.

2. The area of an octagon is 25.54 square units. Find the length of the side.

Solution:

The octagon’s area is 25.54 square units.

$A = 2s^{2}(1\;+\;\sqrt{2})$

$25.54 = 2 \times s^{2}\;(1\;+\;\sqrt{2})$

$s = 2.3$ units

The octagon’s side length is 2.3 units.

3. If a normal octagon’s side is 5 units long, calculate its area and perimeter.

Solution:

An ordinary octagon has equal-length sides. 

The side length in this case is 5 units, or “s.”

Area of a regular octagon $= 2s^{2}\;(1 \;+\; \sqrt{2}) = 2 (5)^{2} (1 \;+\; \sqrt{2}) = 50 (1 \;+\; 2) = 120.71$ square units 

Perimeter of a regular octagon $= 8s = 40$ units

Practice Problems on Octagon Formulas

Frequently Asked Questions about Octagon Formulas