What Are One-step Equations?
One-step equations are algebraic equations that can be solved in one step only. They can be solved in just one step by isolating the variable using the inverse operations. An equation is a mathematical statement that shows that two mathematical expressions are equal.
The most basic and simple algebraic equations consist of one or more variables in math.
An equation consists of two sides, L.H.S. (Left Hand Side) and R.H.S. (Right hand Side) separated by “=” sign. Solving an equation simply means finding the value of the unknown variable.
Consider an equation.
$x\;-\;7 = 93$
Let’s add 7 on both sides to cancel out 7 and isolate the variable.
$x\;-\;7 + 7 = 93 + 7$
Thus, $x = 100$
Wasn’t that simple? This is what we call a “one-step equation.”
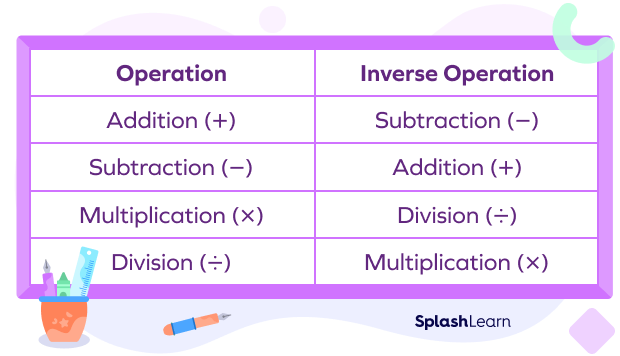
Note: Take note of inverse operations that help in solving the one-step equations.
Definition of One-step Equations
One-step equations are simple algebraic equations that can be solved in just one step.
To solve one-step equations, we determine the value of the variable involved using different properties of equality. The operation you perform on one side of the equation must be carried out on the other side as well, in order to keep the equation balanced. One-step equations may involve integers, fractions, or decimals.
Recommended Games
Rules for One-step Algebraic Equations
While keeping the equation balanced on both sides, the subsequent operations are carried out to isolate the variable. By doing this, LHS continues to be equal to RHS, and eventually, the balance is maintained. There are some rules for one-step algebraic equations. They are as follows:
- One-step Equation with Addition
If the equation involves addition, we can isolate the variable using the inverse operation, which is the subtraction operation.
If we subtract the same number from both sides of an equation, both sides will remain equal. This is the subtraction property of equality.
For example,
$x + 5 = 2$
$\Rightarrow x + 5\;-\;5 = 2\;-\;5$ …subtract 5 from both sides
$\Rightarrow x =\;-\;3$
- One-step Equation with Subtraction
If the equation involves subtraction, we isolate the variable using the addition property of equality. If we add the same number to both sides of an equation, both sides will remain equal.
For example,
$c\;-\;1.1 = 12$
$\Rightarrow c\;-\;1.1 + 1.1 = 12 + 1.1$ …adding 1.1 on both sides
$\Rightarrow c = 13.1$
- One-step Equation with Multiplication
If the equation involves multiplication, we can isolate the variable using division. However, note that we cannot divide by 0.
If we divide both sides of an equation by the same number, both sides will remain equal.
For example,
$4x = 16$
$\frac{4x}{4} = \frac{16}{4}$ …divide both sides by 4
$\Rightarrow x = 4$
- One-step Equation with Division
If the equation involves division, we use multiplication to solve the equation.
If we multiply both sides of an equation by the same number, both sides will remain equal.
For example,
$\frac{x}{4} = \frac{1}{5}$
$\frac{x}{4} \times 4 = \frac{1}{5}\times4$ … multiply both sides by 4
$x = \frac{4}{5}$

Recommended Worksheets
How to Solve One-step Equations
When you’re solving one-step algebraic equations, the goal is to get the variable on one side and all the remaining numbers on the other. We use the inverse operation or the opposite operation to the operation acting on the variable. The inverse operations pairwise are addition and subtraction and division and multiplication.
The steps to solve one-step equations are as follows:
Step 1: Note down the equation.
For example $x\;-\;5 = 10$
An equation will have a variable (x), which denotes an unknown value, and it will also have a constant, which is a number you need to add or subtract from the variable to equal a certain sum or difference.
Step 2: Isolate the variable.
You must conduct an inverse operation to cancel the constants in order to isolate a variable, on one side of the equation.
For example, in the equation, $x \;-\; 5 = 10 , 5$ is subtracted from the variable, so to isolate the variable you must cancel the 5 by adding it on both sides.
Step 3: Adding or subtracting the constant from both sides.
While solving the equation, we have to keep both sides balanced.
So, if you need to add a value to isolate the variable, you must also add that same value to the other side of the equation, also if you need to subtract a value on one side of the equation you have to subtract it from the other side.
In the equation, $x \;-\; 5 = 10$, we need to add 5 on the left as well as on the right.
$x \;-\; 5 + 5 = 10 + 5$
Thus, $x = 15$
Step 4: Verify your solution.
To verify the solution, simply plug in the value of x in the equation.
$x \;-\; 5 = 10$, the value of x as we found out is 15.
Thus, substituting the value, the equation becomes, $15 \;-\; 5 = 10$.
Since this equation is true, your solution is correct.
Similarly, if the variable is multiplied by a number, divide both sides of the equation by the same number to isolate the variable. (If the variable is divided by a number, multiply both sides of the equation by the same number.)
For example, let’s solve an equation. $\frac{x}{6} = 12$
As the variable is divided by 6, to isolate it, you need to multiply by 6.
$6(\frac{x}{6}) = 12\times6$
$\Rightarrow x = 72$
Verifying the solution, as $\frac{72}{6} = 12$ , the solution is correct.
Facts about One-step Equations
- A one-step equation is an equation that requires only one step to solve.
- The most common one-step equations are linear algebraic equations.
- When solving an equation, you may keep the variable on either side of the equation. As long as in the end, the variable that you are solving is isolated on one side with a coefficient of $+1$.
Conclusion
In this article, we have learned how to solve one-step equations, its rules and the steps of solving the equations. Let’s now solve some examples to better understand the concept.
Solved Examples On One-Step Equations
1. Solve this equation with a negative constant: $\;-\;8 + x = 14$
Solution: Since the constant is negative, adding it to both sides will isolate the variable.
$\Rightarrow -8 + x = 14$
$\Rightarrow -8 + x + 8 = 14 + 8$
$x = 22$
Verifying the solution, $-8 + 22 = 14$. The solution is correct.
2. Solve this equation with a negative coefficient: $-4x = 32$
Solution:
Since the variable is multiplied by $-4$, to isolate the variable, you must divide each side by $-4$.
Remember that dividing a positive number by a negative number equals a negative quotient.
$-4x = 32$
$\frac{-4x}{-4} = \frac{32}{-4}$
$\Rightarrow x = \;-\; 8$
Verifying the solution, $-4(\;-8) = 32$. The solution is correct.
3. Jennifer weighed herself on the scale and found her weight to be 120 lbs. Then, she held the cat and stepped on the scale and found the combined weight to be 132 lbs.
Create an equation that models the situation and solve the equation to find c, the cat’s weight.
Solution: To model the following situation, we will create an equation to show the combined weights of Jennifer and cat.
$c + 120 = 132$
To solve for c, we will do the inverse operation of addition and subtract 120 from each side:
$c + 120 \;-\; 120 = 132 \;-\; 120$
$\Rightarrow c = 12$ lbs.
To verify answer we will plug in the values in the equation
$12 + 120 = 132$
Therefore, $c = 12$ lbs is the correct solution.
4. Solve the equation: $10 = \frac{p}{10}$
Solution: Since the variable is divided by 10, we have to isolate it by multiplying it by 10.
$10 = \frac{p}{10}$
$\Rightarrow 10\times10 = \frac{p}{10}\times10$
$\Rightarrow P = 100$
Verifying the solution, $10 = \frac{100}{10}$ . The solution is correct.
Practice Problems On One-Step Equations
Solving One-step Equations
What is the value of x in the equation $5x = 40$?
We will isolate the variable by dividing both sides of the equation by the same number, both sides will remain equal and we will get the solution. For example,$\frac{5x}{5} = \frac{40}{5}$ .Thus, $x = 8$
Identify the equation, where the value of $z = 7$.
We will isolate the variable by dividing both sides of the equation by the same number. $\frac{4z}{4} = \frac{28}{4}$ Thus, $z = 7$.
Identify the equation that does not have a solution at $w = 5$.
Substituting the value in equation, w $-\; 5 = 10$
$5 \;-\; 5 = 10$, which is a false statement.
What equation matches this situation?
Maria had some pencils then bought 4 more. Now she has a total of 10 pencils.
Let's consider pencil as p, Maria has p number of pencils, and she bought 4 more,
i.e., $P + 4$. Now she has a total of ten pencils, which means $P + 4 = 10$.
What is the first step to solve this equation: $2x = 18$.
In the equation above, x is being multiplied by 2. Thus, to isolate the equation, we have to do the inverse and divide both sides of the equation by 2.
Frequently Asked Questions On One-Step Equations
What are the various methods for solving equations?
There are three methods used to solve systems of equations. They are as follows:
- Graphing
- Substitution
- Elimination
What is the difference between one-step equations and two-step equations?
One-step equations require only one step, one inverse operation to be solved and have only one operation. Two-step equations require two inverse operations to solve and have two operations.For eg., $x^2 = 64$ is a one-step equation, while $3x + 2 = 14$ is a two-step equation.
What are linear equations in one variable?
A linear equation in one variable is an equation in which the degree of the variable is 1. These are also known as first degree equations, because the highest exponent on the variable is 1. All linear equations eventually can be written in the form $ax + b = c$, where a, b, and c are real numbers and $a \neq 0$.
What is a one-solution equation?
Some equations have exactly one solution. In these equations, there is only one value for the variable that makes the equation true. You can tell that an equation has one solution if you solve the equation and get a variable equal to a number.
For eg., $5x = 25$ has a variable term, $5x$ on one side of the equation and a constant term, 25, on the other side of the equation. So, it has one solution. Let’s solve the equation to see why.
$5x = 25$ . Divide both sides by 5.
$x = 5$
So, $5x = 25$ has one solution, $x = 5$.
What are equations with no solutions?
If a linear equation has the same variable term but different constant values on opposite sides of the equation, it has no solutions.
For eg., $2x + 4 = 1 + 2x$ has the same variable term, $2x$, but different constant terms, 4 and 1, on opposite sides of the equation. So, it has no solutions. Let’s solve the equation to see why.
$2x + 4 = 1 + 2x$
Subtract 2x from both sides.
$4 = 1$The statement $4 = 1$ is false. So, $2x + 4 = 1 + 2x$ has no solutions.




































