What Is Ordering Decimals?
Arranging decimal numbers in a specific order, i.e, ascending or descending, on the basis of the place values is known as ordering decimals.
Decimals are numbers that have a whole number part and a fractional part divided by a decimal point. Decimals just like any other numbers can be compared and ordered in either ascending or descending order.
Recommended Games
Place Values Chart in Decimals
Comparing and ordering decimals gets easier with the place value chart. The following image shows the place value chart in decimals.
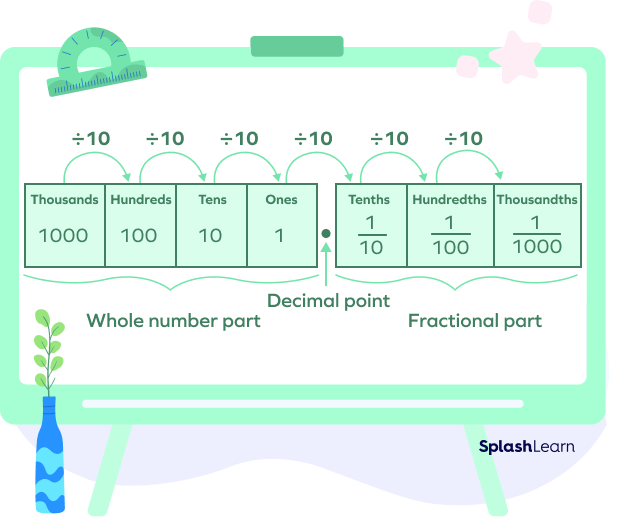
Let’s understand the place values of decimals with an example. Consider the decimal number 1111.1111. Every place has the same digit. However, their place values are different!
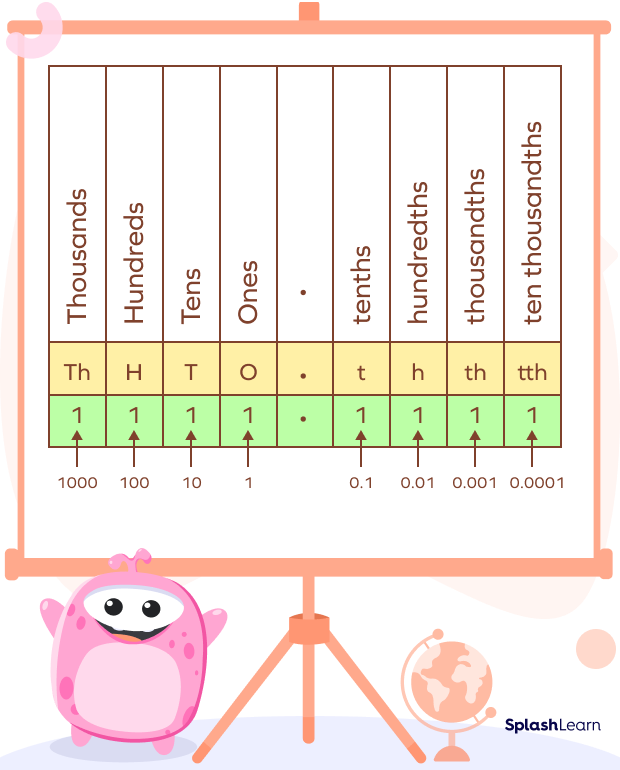
Recommended Worksheets
Steps of Ordering Decimals
To order decimal numbers, we need to first learn how to compare decimal numbers.
Step 1: Use the place value chart!
Write the decimals in the place value chart such that the place values of all the decimals are aligned. The empty boxes at the end of the decimal can be filled with zeroes.
Step 2: Compare the whole number part first.
Always start comparing the digits at the highest place value. Thus, the decimal having the greater whole number part is greater!
For example: Consider the decimals 12.5 and 15.2.
12 is less than 15
Thus, 15.2 is greater than 12.5.
Step 3: Compare the tenths!
If the whole number part matches, compare the next place value, tenth.
Consider the decimals 1.5 and 1.4.
The whole number is 1 in both numbers, thus we will compare the digits after the decimal point—4 and 5.
$5 \gt 4$
Thus, $1.5 \gt 1.4$
Step 4: Compare the hundredths.
If the digits at the tenth place are the same, move to the next place value and compare the digits.
Example: Consider the decimals 23.56 and 23.53.
We will write them in the place value chart for better understanding!
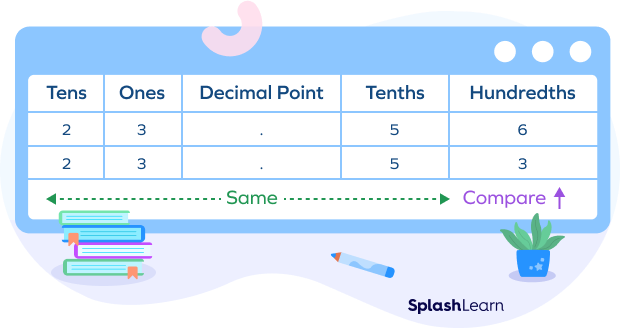
The part 23.5 is the same in both the decimals.
Thus, we compare the digits at the hundredths place, 3 and 6.
$3 \gt 6$ and hence 23.56 is greater than 23.53.
Once you compare the given decimals, ordering them is just the matter of arranging them in increasing or decreasing order.
Different Types of Ordering
There are two different types of the ordering of decimals:
- Ascending order: The order of decimal numbers such that, in a sequence, each decimal number is not less than the previous number, or we can also say that the terms are either equal or greater than the previous number.
- Descending order: The order of decimal numbers such that, in a sequence, each decimal number is not more than the previous number, or we can also say that the terms are either equal or lesser than the previous number.
How to Order Decimals
To order decimals, we will first compare the decimals. Write the decimals in the place value chart in order to compare them. To arrange them in ascending order, we write them from the smallest to the greatest. To arrange them in descending order, we write them from the greatest to the smallest.
Example 1: Order decimals from least to greatest.
5.31, 6.88, 7.21, 6.45
Compare the digits at ones place: we get $7 \gt 6 \gt 5$
Thus, 7.21 is the greatest decimal and 5.31 is the smallest.
To compare 6.88 and 6.45, compare the digits at the tenths place.
Since $4 \lt 8$, we get $6.45 \lt 6.88$
Thus, $5.31 \lt 6.45 \lt 6.88 \lt 7.21$
The given decimals can be arranged in ascending order as: 5.31, 6.45, 6.88, 7.21
Ordering Decimals in Ascending Order
To order the decimal numbers in ascending order, we will arrange the numbers in such a way that each decimal number is smaller than the next decimal number. It means increasing order. How can we order decimals from least to greatest? Simply compare them using the place value chart and start listing them in the increasing order.
Ordering Decimals in Descending Order
To order the decimal numbers in descending order, we will arrange the numbers in such a way that each decimal number is larger than the next decimal number. It means decreasing order.
Fun Facts!
- The decimal numbers are of three types—terminating, non-terminating repeating, and non-terminating non-repeating.
- The terminating and non-terminating repeating decimal numbers are classified as rational numbers.
- The non-terminating non-repeating decimal numbers are classified as irrational numbers.
Conclusion
This article gives an insight into the concept of decimals, teaching us how to compare decimals and how to arrange them in ascending or descending order. Ordering decimals is a part of daily life, which we see commonly while comparing amounts of some objects and the values are in decimal numbers.
Solved Examples on Ordering Decimals
1. Compare and arrange the following decimal numbers in descending order:
0.51, 0.45, 3.22, 1.67, 0.452.
Solution:
Write the numbers in the place value chart. Start comparing the digits at the highest place value, that is, the ones place.
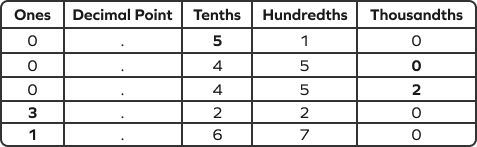
Comparing the ones place digits, we get
$1.67 \lt 3.22$
For the decimals 0.51, 0.45, and 0.452, we compare the tenths, hundredths, and thousandths place.
$0.51 \lt 0.450 \lt 0.452$
The numbers in descending order are:
$3.22 \gt 1.67 \gt 0.51 \gt 0.452 \gt 0.45$
2. Which one is greater—1.01 or 1.10?
Solution:
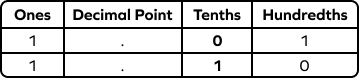
The numbers 1.01 and 1.10 both have the same whole number part 1.
We will compare the digits at the tenths place, which are 0 and 1.
$0 \lt 1$
Thus $1.10 \gt 1.01$.
3. Arrange the given decimals in ascending order.
0.96, 6.01, 0.0009, 0.93
Solution: Start comparing the digits at the highest place value.
We get that 6.01 is the greatest decimal.
Between 0.96, 0.93 and 0.0009, we get
$0.93 \lt 0.96 \lt 0.0009$
Thus, the given decimals can be written in the ascending order as:
$0.93 \lt 0.96 \lt 0.0009 \lt 6.01$
Practice Problems on Ordering Decimals
Ordering Decimals: Definition, Types, Examples
Which one of the following is the same as 1.1?
$1.1 = 1.10$
The empty place at the end of the decimal can be filled with zeros.
Which of the following represents an ascending order of decimal numbers?
Ascending order means that the numbers are arranged in increasing order of their value. Thus, 1.2, 1.4, 2.5 is the only correct answer.
Which one of the following decimals is the smallest?
We will compare the numbers by their place value, and after comparison, we find that 0.009 is the smallest among all the options.
Choose the correct sign.
0.119 ____ 0.091
Both decimals have 0 at their ones place.
Compare the tenths place: $1 \gt 0$
Thus,$0.119 \gt 0.091$
Frequently Asked Questions on Ordering Decimals
What are terminating decimal numbers?
Terminating decimal numbers are numbers that have a finite number of digits after the decimal point, and they terminate after certain decimal places. For example, 0.5, 1.2345, etc.
What is the significance of ordering?
Ordering is an important part of life. Without ordering, analysis of sufficiently large data is almost impossible. We see ordering in almost every part of our life, like the order of events in a party, the order of items on a shelf, etc.
What are rational numbers in terms of decimals?
Rational numbers are numbers that have either terminating or non-terminating repeating decimal forms. These numbers can be represented as a fraction where the denominator is non-zero.
What are decimal fractions?
Decimal fractions are fractions whose denominator is a power of 10.




































