Percent to Decimal: Definition with Examples

What is Percent to Decimal Conversion?

To convert a percent to decimal, divide the percentage value by 100 and remove the $\%$ sign. Decimals are numbers that consist of a whole number part and a fractional part separated by the decimal point.

Check out the Percent to Decimal Calculator available online. It converts any percentage value into a decimal instantly! 

What Is a Percent?

“Percent” means “per 100.” A percent means a fraction with denominator 100. 

1% is equal to “one hundredth” or $\frac{1}{100}$.

30% is equal to “thirty hundredths” or $\frac{30}{100}$. 

We use percentages to represent parts out of 100 equal parts. 

What Is a Decimal?

​​A decimal is a number that consists of a whole and a fractional part. Decimal numbers lie between integers and represent numerical value for quantities that are whole plus some fractional part.

Percent to Decimal Conversion: Definition

Percent to decimal conversion is a method of converting a percent value to decimal value by dividing the percentage by 100 and removing the $\%$ sign. 

Division by 100 shifts the decimal point two positions to the left. Thus, to convert percent to decimal, simply shift the decimal point two positions to the left and remove the $\%$ sign.

Example 1: Convert 15 percent to decimal.

Note that $15\% = 15.0\ %$

$15\% = \frac{15}{100} = 0.15$

Example 2: Convert 10 percent to decimal.

$10\% =  \frac{10}{100} =  110 = 0.1$

Try to visualize such percent to decimal conversions on a number line. Need help? Take a look at the image below!

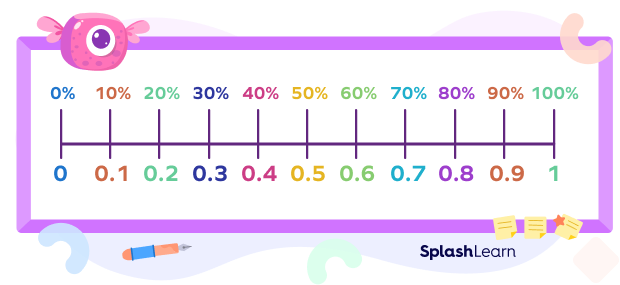
How to Convert Percentage into Decimal

Let’s understand the steps to convert percentage into decimal.

Step 1: Remove the percentage sign $(\%)$ from the number by dividing the number by 100.

Step 2: Shift the decimal point two places towards the left.

Example 1: Convert $20\%$ to a decimal. 

$20\%$ means 20 parts out of 100 equal parts.

$20\% = \frac{20}{100} = \frac{2}{10} = 0.2$

Example 2: Convert $4.5\%$ to decimal.

Shift the decimal point two places to the left. Remove the % sign.

So, $4.5\% = 0.045$.

Example 3: Convert $85\%$ to decimal.

How to Convert Fraction Percent into Decimal

A percent given in the fractional form, such as $\frac{2}{5}\%$ or $\frac{14}{3}\%$, can also be converted into decimal form. Suppose we have to convert 112% into decimal, we follow the steps given below:

Step 1: The is given in the mixed fraction form. So, we will convert it to an improper fraction first. 

$1\frac{1}{2}\% = 32\%$

If it already exists in the fraction form, go to step 2.

Step 2: Convert the given fraction to a decimal by dividing the numerator with the denominator. 

Here, $\frac{3}{2} = 1.5$

Thus, $\frac{3}{2}\% = 1.5\%$.

Step 3: Remove the percent sign and shift the decimal point two places to the left. 

In this case, we get

$1\frac{1}{2}\% = \frac{3}{2}\% = 1.5\% = 0.015\%$

Percent to Decimal Chart

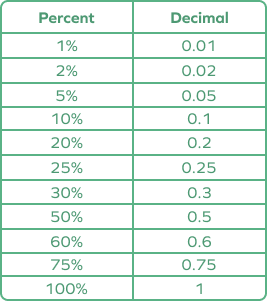
Percent to Decimal Conversion: Visual Example

Solved Examples on Percent to Decimal Conversion

1. Convert $25\%$ to decimal.

Solution: 

Remove the percent sign and divide the number by 100. To get the answer, shift the decimal point.

$25\% = \frac{25}{100} = 0.25$

2. What will be the decimal value for $90\%$?

Solution: 

Remove the percent sign. Shift the decimal point two places towards the left.

$90\% = \frac{90}{100} = 0.90$.

3. Mark ate 30% of the apple pie while Sherry ate $20\%$ of it. Find the portion of cake left in decimals, using the percent to decimal conversion.

Solution: There is one apple pie, so the whole is 1. Now, Mark ate $30\%$ of the cake, which means he ate 0.3 portions. Similarly, Sherry ate $20\%$, which is equivalent to 0.2 portions of the cake. 

The portion of the cake left is $[1 \;–\; (0.3 + 0.2)]$.
$\Rightarrow 1 \;–\; 0.5$
$\Rightarrow 0.5$
Therefore, 0.5 portions of the apple pie is left.

4. Convert $1\frac{3}{2}\%$ into decimal. 

Solution: 

$1\frac{3}{2}\% = \frac{5}{2}\%$

$\frac{5}{2} = 2.5$

So, $\frac{5}{2}\% = 2.5\%$

Remove the percent sign and divide 2.5 by 100.

$2.5\% = \frac{2.5}{100}$

Shifting the decimal point two places towards the left, we get

$2.5\% = \frac{2.5}{100} = 0.025$

Practice Problems on Percent to Decimal Conversion

Frequently Asked Questions on Percent to Decimal Conversion