Convert Percent to Fraction –  Definition, Steps, Examples

What Is Percent to Fraction Conversion?

Percent to fraction conversion refers to converting a percentage value to fraction form.

The meaning of the word “percent” is “per 100.” A fraction represents the parts of a whole. A percent is a fraction whose whole is always 100. In other words, we can say that the denominator of a percentage is 100, which implies a percent can be converted into a fraction.

Example: Suppose that you eat $50\%$ of a whole pizza. In other words, you eat $\frac{1}{2}$ fraction of the pizza.

How can we turn a percent into a fraction? Here, we simply divided 50 by 100, removed the $\%$ sign and simplified the fraction! Let’s understand the steps in detail.

Steps to Convert Percent to Fraction

Writing percentages as fractions is pretty straightforward. To convert percent to a fraction, there are only three easy steps. Let’s understand how to turn a percent into a fraction using three simple steps.

Step 1: Remove the percent sign $\%$.

Step 2: Divide the number by 100.

Step 3: Reduce the resulting fraction.

How to Convert a Percent to a Fraction

In accordance with the steps for converting a percent to a fraction, remove the $\%$ sign, divide the number by 100. Also, simplify the fraction if required. 

Example 1: Convert $97\%$ to a fraction. 

$97\% = \frac{97}{100}$ 

Example 2: What is the fraction form of $75\%$?

$75\% = \frac{75}{100}$

Simplify further by dividing both numerator and denominator by 25.

$75\% = \frac{75}{100} = \frac{3}{4}$

Visualize Percent to Fraction Conversion

The below example shows some standard percentage-to-fraction conversions.

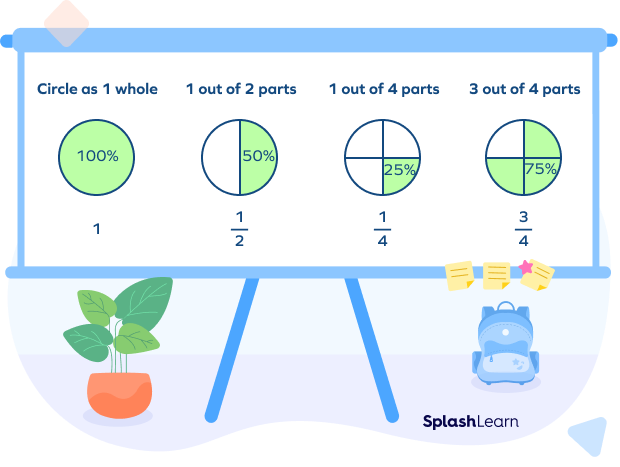
Percent-to-Fraction Conversion: Types

The percent-to-fraction conversion of different types of numbers associated with percentages can be categorized as

• Whole number percent to fraction
• Mixed number percent to fraction
• Decimal number percent to fraction

Let’s discuss each of these conversions in detail.

Whole Number Percent to Fraction

As mentioned earlier, the following steps can be used to convert the whole percent to a fraction.

Step 1: Eliminate the percent sign “%” and divide the number by 100.

Step 2: Reduce the resulting fraction to make a simple fraction.

Examples:

$20\% = \frac{20}{100} = \frac{1}{5}$  

$80\% = \frac{80}{100} = \frac{4}{5}$

$60\% = \frac{60}{100} = \frac{3}{5}$

7 percent as a fraction $= \frac{7}{100}$

3 percent as a fraction $= \frac{3}{100}$

20 percent as a fraction $= \frac{7}{100}$

25 percent as a fraction $= \frac{25}{100} = \frac{1}{4}$

40 percent as a fraction $= \frac{40}{100} = \frac{2}{5}$

Mixed Number Percent to Fraction

What can we do if we get percents with fractions instead of numbers? The following steps can be used to convert the mixed number percent to fraction.

Step 1: First convert mixed fractions into improper fractions.

Step 2: Eliminate the percent sign “$\%$” and divide the number by 100.

Step 3: Reduce the resulting fraction to make the fraction in its simplest form.

Example: Convert $2\frac{3}{5}\%$ to a fraction.

$2\frac{3}{5} = \frac{(5\times2) + 3}{5} = \frac{13}{5}$

$\frac{13}{5}\% = \frac{\frac{13}{5}}{100} = \frac{13}{5}\times\frac{1}{100} = \frac{13}{500}$

Decimal Number Percent to Fraction

The following steps can be used to convert the decimal percent to fractions.

Step 1: Eliminate the percent sign “$\%$” and divide the number by 100.

Step 2: For each number after the decimal point, multiply the top and bottom by 10 if there is only one number after the decimal point. (If there are two decimal digits, multiply by 100, and so on.)

Step 3: Reduce the resulting fraction to make a fraction in its simplest form.

Example: Convert 44.75% to a fraction.

Remove the$\%$ sign and divide 45.7 by 100.

$44.75\% = \frac{44.75}{100}$

Eliminate the decimal point by multiplying the numerator and denominator by 100.

$\frac{44.75}{100}\times\frac{100}{100} = \frac{4475}{10000}$

Percent-to-Fraction Conversion Table

Percent	Fraction
$1\%$	$\frac{1}{100}$
$2\%$	$\frac{1}{50}$
$4\%$	$\frac{1}{25}$
$5\%$	$\frac{1}{20}$
$8.5\%$	$\frac{17}{200}$
$10\%$	$\frac{1}{10}$
$12.5\%$	$\frac{1}{8}$
$16.6\%$	$\frac{83}{500}$
$20\%$	$\frac{1}{5}$
$25\%$	$\frac{1}{4}$
$30\%$	$\frac{3}{10}$
$33\%$	$\frac{33}{100}$
$40\%$	$\frac{2}{5}$
$50\%$	$\frac{1}{2}$
$55.75\%$	$\frac{223}{400}$
$60\%$	$\frac{3}{5}$
$66\%$	$\frac{33}{50}$
$70\%$	$\frac{7}{10}$
$75\%$	$\frac{3}{4}$
$80\%$	$\frac{4}{5}$
$90\%$	$\frac{9}{10}$
$100\%$	$1$

Facts about Percent to Fraction Conversion

Solved Examples on Percent to Fraction

1. Convert $12\%$ to a fraction.

Solution:

Eliminate the percent sign “$\%$” and divide the number by 100.

$12\% = \frac{12}{100}$

Now, reduce the resulting fraction to make a simple fraction.

$\Rightarrow 12\% = \frac{12}{100} = \frac{12 \div 4}{25 \div 4} = \frac{3}{25}$

Hence, $12\% = \frac{3}{25}$

2. Convert $6\frac{4}{5}\%$ into fractions.

Solution:

First convert the mixed fraction $6\frac{4}{5}$ into an improper fraction.

$6\frac{4}{5} = \frac{34}{5}$

Eliminate the percent sign “$\%$” and divide the fraction by 100.

$6\frac{4}{5}\% = \frac{\frac{34}{5}}{100} = \frac{34}{5\times100} = \frac{34}{500}$

Now, reduce the resulting fraction to the simplest form.

$\Rightarrow 6\frac{4}{5}\% = \frac{34}{500} = \frac{17 \times22}{50\times 2} = \frac{17}{250}$

Hence, the fraction form of $6\frac{4}{5}\%$ is $\frac{17}{250}$.

3. Convert $15.5\%$ into fractions.

Solution:

Eliminate the percent sign “$\%$” and divide the number by 100.

$15.5\% = \frac{15.5}{100}$

Multiply the numerator and denominator by 10.

$15.5\% = \frac{15.5}{100}\times\frac{10}{10} = \frac{155}{1000}$

Reduce the resulting fraction to make a fraction in its simplest form.

$15.5\% = \frac{155}{1000} = \frac{5\times31}{5\times200} = \frac{31}{200}$

Hence, the fractional form of $15.5\%$ is $\frac{31}{200}$.

4. What are the steps to convert $5.25\%$ into a fraction?

Solution:

Given percentage is $5.25\%$.

Step 1: Eliminate the percent sign “$\%$” and divide the number by 100.

$5.25\% = \frac{5.25}{100}$

Step 2: Multiply the top and bottom by 100.

$5.25\% = \frac{5.25}{100}\times\frac{100}{100} = \frac{525}{10000}$

Step 3: Reduce the resulting fraction to make a fraction in its simplest form.

$5.25\% = \frac{525}{10000} = \frac{5\times5\times21}{5\times5\times400} = \frac{21}{400}$

Hence, the fractional form of $5.25\%$ is $\frac{21}{400}$.

5. Noah finished $85\%$ of the math notebook. What fraction of the notebook is finished?

Solution:

Eliminate the percent sign “$\%$” and divide the number by 100.

$85\% = \frac{85}{100}$

Now, reduce the resulting fraction to make a simple fraction.

$\Rightarrow 12\% = \frac{85}{100} = \frac{5 \times 17}{5 \times 20} = \frac{17}{20}$

Thus, $\frac{17}{20}$ part of the notebook is finished.

Practice Problems on Percent to Fraction Conversion

Frequently Asked Questions on Percent to Fraction Conversion