What Is a Perfect Number?
Perfect numbers in math are the numbers (positive integers) that can be expressed as the sum of their factors (excluding the number itself).
Factors of a number are the numbers that divide a given number exactly without leaving a remainder. A factor of a number is always less than or equal to the number.
Recommended Games
Perfect Numbers Definition
A perfect number is defined as a positive integer that can be expressed as the sum of its proper factors (factors except for the number itself).
Perfect number examples: 6, 28, 496
The factors of 6 are 1, 2, 3 and 6.
We can write $6 = 1 + 2 + 3$.
The smallest perfect number is 6.
When the sum of all the divisors of a number is equal to twice the number, the number is known as complete number. All the perfect numbers are also complete numbers.
Recommended Worksheets
Theorem of Even Perfect Numbers
An even natural number N is perfect if and only if it is of the form $N = 2^{n-1}(2^n\;−\;1)$, where $2^n\;−\;1$ is a prime number.
Example: Put $n = 2\; in(2^n\;−\;1)$
$2^n\;−\;1 = 2^2\;−\;1 = 3$ …a prime number
Thus, $2^{n-1}(2^n\;−\;1) = 2^{2-1}\;(3) = 6$ …a perfect number
How to Find a Perfect Number
According to Euclid, there is an expression that can be used to check if a number is a perfect number. Around 2000 years ago, Euclid showed that any even perfect number can be represented by,
If $(2^n\;-\;1)$ is a prime number, then $2^{n-1}(2^n\;-\;1)$ is a perfect number.
In other words, $2^{n-1}(2^n\;-\;1)$ is a perfect number, if (2n-1) is a prime number.
Let’s find a value of “n” for which $(2^n\;-\;1)$ is prime. All such numbers will help us form a list of perfect numbers.
| n | $2^{n-1}$ | $(2^n\;-\; 1)$ | $2^{n-1} \times (2^n\;-\; 1)$ |
|---|---|---|---|
| 1 | 1 | 1 | – |
| 2 | 2 | 3 (prime number) | 6 (perfect number) |
| 3 | 4 | 7 (prime number) | 28 (perfect number) |
| 4 | 8 | 15 (not a prime number) | – |
| 5 | 16 | 31 (prime number) | 496 (perfect number) |
| 6 | 32 | 63 (not a prime number) | – |
| 7 | 64 | 127 (prime number) | 8128 (perfect number) |
| 8 | 128 | 255 (not a prime number) | – |
| 9 | 256 | 511 (not a prime number) | – |
| 10 | 512 | 1023 (not a prime number) | – |
Perfect Numbers Chart
A few perfect numbers are 6, 28, 496 and 8128. Let us observe their divisors and their sum through the table given below. Their sum results in the number itself.
| Perfect Number | Sum of Divisors |
|---|---|
| 6 | $1 + 2 + 3 = 6$ |
| 28 | $1 + 2 + 4 + 7 + 14 = 28$ |
| 496 | $1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496$ |
| 8128 | $1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128$ |
Perfect Numbers From 1 to 100
There are only two perfect numbers between 1 to 100, which are 6 and 28.
History of Perfect Numbers
The history of perfect numbers and its study goes back to the ancient Egyptians, Greeks, and also the followers of Pythagoras.
The smallest perfect number found out was 6, which encouraged people to study the properties of the perfect numbers. The early definition of perfect numbers was given as: a perfect number n is a positive integer, which is equal to the sum of its factors, excluding n itself.
Facts about Perfect Numbers
- For any number, the number itself is the greatest factor. A proper factor of a number is any factor of the number except the number itself.
- There’s a quote from Philo of Alexandria, a Jewish Philosopher from Egypt (born 25 BCE) that says: The world was created in 6 days and the moon orbits in 28 days because 6 and 28 are perfect.
- A Mersenne Prime is a prime number that is one less than a power of two. That means it is a prime number of the form $M_n = 2^n \;−\; 1$ for some integer n. Examples: 3, 7, 31
Solved Examples on Perfect Numbers
1. Is 6 a perfect number?
Solution:
Yes. $6 = 1 + 2 + 3$
where 1, 2 and 3 are the proper factors of 6.
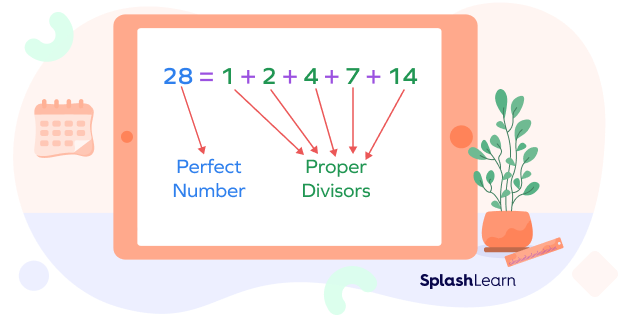
2. Check whether 28 is a perfect number or not by finding the sum of its factors.
Solution:
The factors of 28 are 1, 2, 4, 7, 14 and 28.
Proper factors of 28 are 1, 2, 4, 7, and 14.
Sum of proper factors $= 1 + 2 + 4 + 7 + 14 = 28$.
Thus, 28 is a perfect number.
3. Is 15 a perfect number?
Solution:
Factors of 15 are 1, 3, 5 and 15.
$1 + 3 + 5 = 9 \neq 15$.
Thus, 15 is not a perfect number.
4. If we substitute $n = 11$ in $2^n\;-\;1$, will it give us a perfect number?
Solution:
$n = 11$
If $(2^n\;-\;1)$ is a prime number, then $2^n\;-\;1(2^n\;-\;1)$ is a perfect number.
So, $2^11\;-\;1 = 1023$ which is not a prime number.
So, it will not give us a perfect number.
5. Check whether 39 is a perfect number by finding the sum of its factors.
Solution:
Factors of $39 = 1, 3, 13$ and 39.
Proper factors of $39 = 1, 3, 13$
$1 + 3 + 13 = 17 \neq 39$.
Thus, 39 is not a perfect number.
Practice Problems on Perfect Numbers
What Are Perfect Numbers? Definition, List, Formula, Examples
Which of the following is a perfect number?
Only 28 can be written as the sum of its proper factors
$28 = 1 + 2 + 4 + 7 + 14$
Thus, 28 is a perfect number.
2. Which of the following is the smallest perfect number?
The smallest perfect number is 6.
Which of the following is not a perfect number?
Factors of 27 are 1, 3, 9, and 27.
$1 + 3 + 9 = 13 \neq 27$.
A perfect number can be written as the ____ of its proper factors.
A perfect number can be written as the sum of its proper factors.
Frequently Asked Questions on Perfect Numbers
What is the difference between perfect numbers and perfect squares?
A perfect square is a number, which can be expressed as the square of a number from the same number system whereas a perfect number is a number, which can be expressed as the sum of its factors except itself.
Are all perfect numbers even?
The perfect numbers found till date have been even. There is no evidence of odd perfect numbers.
How many perfect numbers are known?
So far, 51 perfect numbers are known till date.
Why is 1 not a perfect number?
A perfect number can be written as the sum of its proper factors. The only factor of 1 is 1. So, 1 is not a perfect number.
What are the first 5 perfect numbers?
The first 5 perfect numbers are 6, 28, 496, 8128, and 33550336.




































