Point Slope Form: Definition, Derivation, Facts, Examples, FAQs

What Is Point Slope Form?

The point slope form of the equation of a line refers to the equation of a line with slope m and passing through the point with coordinates (x₁, y₁). It can be given as

(y − y₁) = m(x − x₁)

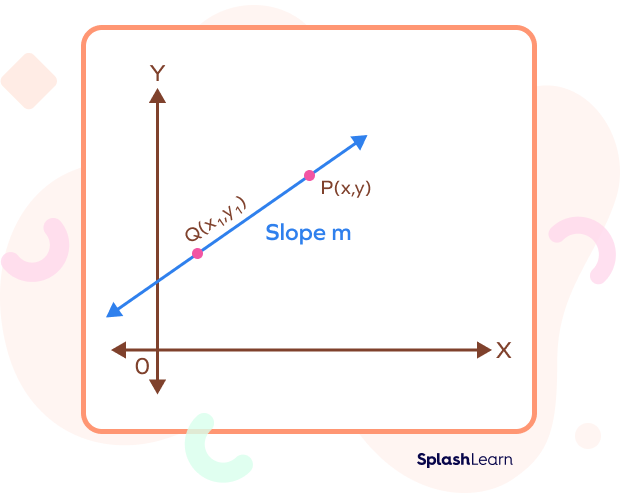
We can write the equation of a line using different forms such as slope-intercept form, two-point form, etc., based on the information known to us. The point slope form, as the name suggests, uses the slope of the line and the coordinates of any point lying on the line to define the equation of the line.

What is a Slope?

The slope or the gradient of a line is denoted by m. It tells us about the steepness of a line. It is defined by the rise over run ratio. 

If a line passes through the points (x₁, y₁) and (x₂, y₂), its slope can be defined as

Slope $= m = \frac{Rise}{Run} = \frac{Change\; in\; y}{Change\; in\; x} = \frac{(y2 − y_{1})}{(x2 − x_{1})}$

Point Slope Formula

The point slope form formula of the equation of a straight line is given by 

(y − y₁)= m(x − x₁) 

where,

• (x, y) represents the coordinates of any point on the line.
• (x₁, y₁) represents the coordinates of a given fixed point on the line.
• m is the slope of the line.

Derivation of Point Slope Formula

Let us consider a line with slope m . Assume that (x₁, y₁) is a fixed and known point on the line and (x, y) is just an ordinary point. 

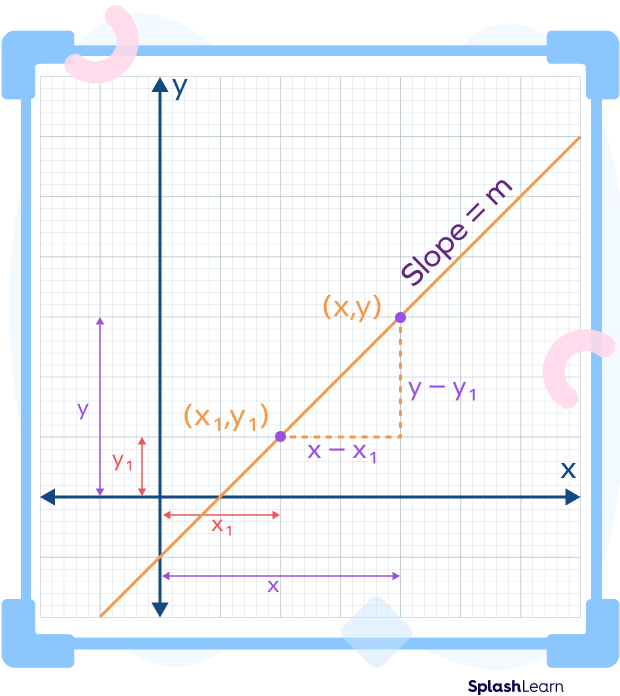
Let’s understand how to find m in point slope form. We know that the formula for the slope of a line passing through the points (x₁, y₁) and (x₂, y₂) is given by

Slope $= m = \frac{Rise}{Run} = \frac{Change \;in\; y}{Change \;in\; x} = \frac{(y2 − y_{1})}{(x2 − x_{1})}$

Suppose that we know the coordinates of only one point (x₁, y₁). Let the coordinates of the other random point on the line be (x, y). We can rewrite the formula for the slope with one point as

$\Rightarrow m = \frac{(y − y_{1})}{(x − x_{1})}$

On cross multiplication, we get the point-slope formula as

(y − y₁) = m(x − x₁)

Equation of a Line with Slope and Coordinates of a Point

We can find the equation of a line with slope m and coordinates of a point (x₁, y₁) using the point slope formula.

Example: Find the equation of a line with slope −2 such that the point is (2, 3) lies on the line. 

Here, (x₁, y₁) = (2, 3) is the point on the line.

m = −2 is the slope.

Using the point slope form, we get 

(y − y₁) = m(x − x₁)

(y − 3) = (− 2)(x − 2))

y− 3 = −2x + 4

y = (− 2)x + 7

\Rightarrow 2x + y = 7

Deriving Two Point Form Using Point Slope Form

Consider a case where the slope of the line is not given. We only know the coordinates of two points on the line. Let the two points be (x₁, y₁) and  (x₂, y₂). 

In such a case, we will first find the slope by:

$m = \frac{(y_{2} − y_{1})}{(x_{2} − x_{1})}$

Now that we know the slope of the line, we can find the the equation of a line by using the Point Slope Form (y − y₁) = m(x − x₁). 

(You can use the coordinates of any of the given two points here.)

(y − y₁) = m(x − x₁)

(y − y₁) $= \frac{(y_{2} − y_{1})}{(x_{2} − x_{1})} (x − x_{1})$

This is called two-point form.

Example: Find equation of a line where (− 1, 2) and (3, 0) are two points on the line.

The equation of the line is:

 (y − 0) $= \frac{0 − 2}{3− (− 1)} (x − (− 1))$

$y = \frac{− 2}{3} (x + 1)$

$\Rightarrow 3y = −2x − 2$

$\Rightarrow 2x − 3y = −2$

Facts about Point Slope Form

Conclusion

In this article, we learned how to find the equation of a straight line using the slope point form. We discussed its formula, derivation by visualizing it on a graph, and examples. Let’s check our understanding by solving a few examples and practice problems based on the Point Slope Form.

Solved Examples on Point Slope Form

1. Find the slope and equation of a line if the coordinates of two points on the line are (0,-1) and (3,-5).

Solution: 

Let (x₁, y₁) = (0, −1) and (x₂, y₂) be (3, − 5). 

Slope $(m) = \frac{(y_{2} − y_{1})}{(x_{2} − x_{1})} = \frac{− 5− (− 1)}{3 − 0} = \frac{− 5 + 1}{3} = \frac{− 4}{3}$ 

Let’s use (x₁, y₁) = (0, −1) and m $= \frac{− 4}{3}$ to find the equation of the line in the slope point form.

(y − y₁) = m(x − x₁)

$(y− (− 1)) = \frac{− 4}{3}(x − 0)$

$(y + 1) = \frac{− 4}{3}x$

3y + 3 = − 4x

4x + 3y = − 3

2. Find the equation of a line passing through the point (3, 6) and has a slope $− \frac{1}{2}$.

Solution: 

Slope $(m) = − \frac{1}{2}$

Let the fixed point be (x₁, y₁) = (3, 6).

Point Slope Form: (y − y₁) = m(x − x₁)

The equation of the line will be: 

(y − 6) $= (− \frac{1}{2}) (x − 3)$

2(y − 6)= − 1(x − 3)

2y − 12 = − x + 3

x + 2y = 15

3. What is the equation of a line with slope -5 and passing through the point (− 7, 1)?

Solution: 

Slope (m) $= − \frac{1}{2}$

Let the fixed point be (3, 6).

Point Slope Form: (y − y₁) = m(x − x₁)

The equation of the line will be: 

(y − 6) $= (− \frac{1}{2})(x \;-\; 3)$

2(y − 6) = − 1(x − 3)

2y − 12 = − x + 3

x + 2y = 15

4. Find the equation of a line passing through the points (2,− 3) and (−1, 10).

Solution: 

Let (x₁, y₁) = (2, − 3) and (x₂, y₂) be (−1, 10).

The point slope linear equation will be:

 $(y − y_{1}) = \frac{(y_{2} − y_{1})}{(x_{2} − x_{1})} (x − x_{1})$

$(y− (− 3)) = \frac{(10− (− 3))}{(− 1 − 2)}(x − 2)$

$y + 3 = \frac{1}{3} −3(x − 2)$

− 3(y + 3) = 13(x − 2)

− 3y − 9 = 13x − 26

13x + 3y = 17

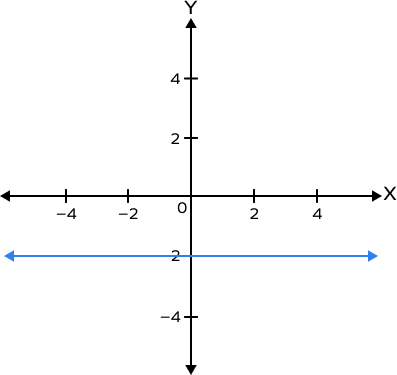
5. What is the equation of a line with slope 0 and passing through the point (7, − 2)? What can you say about this line? Graph the line.

Solution: 

Let (x₁, y₁) = (7, − 2) and m = 0.

Point Slope Form: (y − y₁) = m(x − x₁)

The point slope form equation of the line will be:

 (y − (− 2)) = 0 (x − 7)

(y− ( −2)) = 0

y + 2 = 0

y = −2

As the slope of the line is 0, it is a horizontal line parallel to the x-axis. Also, since the equation of the line is y = −2, it is a horizontal line passing through the point (0, −2). The value of the y-coordinate y = −2 remains constant.

Practice Problems on Point Slope Form

Frequently Asked Questions about Point Slope Form