Properties of Whole Numbers: Definition with Examples

What Are the Properties of Whole Numbers?

Properties of whole numbers include certain rules or facts that help us perform basic arithmetic operations like addition and multiplication. Using the properties of whole numbers, one can calculate mathematical expressions and solve them quickly.

Properties of whole numbers make it easier to perform basic arithmetic operations like addition, subtraction, and multiplication on the whole numbers. Using these properties, we can simplify calculations and solve math problems in less time.

What Are Whole Numbers?

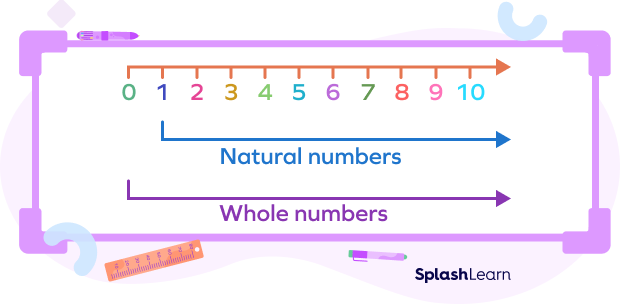
A set of whole numbers include natural numbers and zero (0).

A set of whole numbers is represented by the letter W.

$W = \left\{0, 1, 2, 3, 4,…\right\}$. 

Whole numbers do not include fractions, decimals, or negative integers. We can also describe whole numbers as the union of the natural numbers (or positive integers) and 0.

List of Properties of Whole Numbers

Properties of whole numbers are as follows:

1. Closure Property
2. Commutative Property of Addition and Multiplication
3. Associative Property of Addition and Multiplication
4. Distributive Property of Multiplication over Addition
5. Identity Property

The chart of properties of whole numbers summarizes these properties as shown below.

Now, let’s discuss the properties of whole numbers with examples.

Closure Property

The closure property of whole numbers states that the addition or multiplication of two whole numbers will always give us a whole number. In other words, whole numbers are closed under multiplication and addition. 

Consider a and b to be two whole numbers such that a, $b \in W$, then,

$a + b \rightarrow W$

$a \times b \rightarrow W$

The closure property does not apply over subtraction and division of whole numbers since the difference and division between two whole numbers might not give us a whole number.

Example: 

$4\;-\;7 = \;-3$, negative integer

$\frac{4}{7} = 0.5714$, a decimal number.

Also, division by the whole number zero $(0)$ gives us an undefined number.

Commutative Property of Addition and Multiplication

The commutative property of whole numbers states that even if we change the order of the two whole numbers in addition and multiplication, the sum or the product stays the same. In other words, one can add or multiply two whole numbers in any order and will get the same answer. 

Consider two whole numbers A and B, the commutative property states that:

for all a, $b \in W$,

$a + b = b + a$           … addition

and

 $a \times b = b \times a$ … multiplication

For example, 

in addition: $1 + 4 = 4 + 1 = 5$,

and in multiplication: $2 \times 4 = 4 \times 2 =8$.

The commutativity does not apply over subtraction and division of two whole numbers. The reason being, if we change the order of the numbers during subtraction, the resulting answer will change in sign.

Example: 

$4 \;-\; 2 = 2$ and $2 \;-\; 4 = \;-2$

$\frac{4}{2} = 2$ and $\frac{2}{4} = 0.5$

Associative Property of Addition and Multiplication

Under the associative property, the sum or product obtained of three or more numbers remains the same even if we rearrange or regroup numbers in different order.

Consider three whole numbers a, b, and c. The associative property states that:

$a+ \left[b + c\right]= \left[a + b\right] + c$ …addition

$\left[a \times b\right] \times c = a \times \left[b \times c\right]$ …multiplication

Example:

• $3 + \left[5 + 7\right] = \left[3 + 5\right] + 7$

$3 + 12 = 8 + 7$

$15 = 15$

• $3 \times \left[5 \times 7\right] = \left[3 \times 5\right] \times 7$

$3  \times  35 = 15  \times  7$

$105 = 105$

Associative property does not apply over subtraction and division of two whole numbers.

Distributive Property of Multiplication Over Addition and Subtraction

The distributive property of multiplication over addition states that multiplication is distributive over the sum of two or more whole numbers. 

Consider three whole numbers a, b, and c. 

The associative property states that:

  $a \times \left[b + c\right] = \left[a \times b\right] + \left[a \times c\right]$ …multiplication over addition

  $a \times \left[b \;-\; c\right] = \left[a \times b\right] \;-\; \left[a \times c\right]$ …multiplication over subtraction

Example of distributive property of multiplication over addition:

$4 \times \left[6 + 8\right] = \left[4 \times 6\right] + \left[4 \times 8\right]$

$4 \times 14 = 24 + 32$

$56 = 56$

Example of distributive property of multiplication over subtraction:

$5 \times \left[4 + 2\right] = \left[5 \times 4\right] + \left[5 \times 2\right]$

$5 \times 6 = 20 + 10$

$30 = 30$

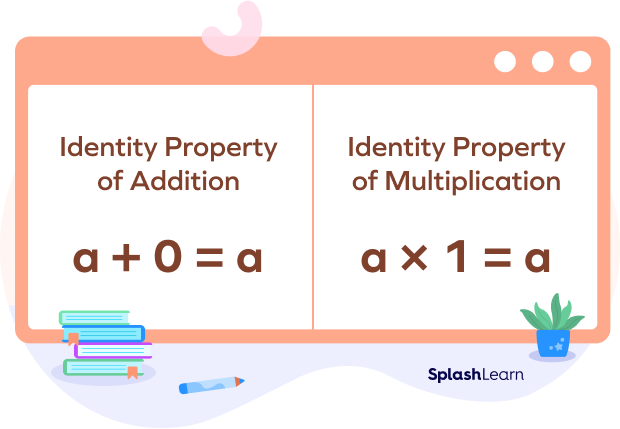
Identity Property

Additive Identity:

This property states that when zero is added to a whole number, the result is the whole number itself. This makes zero the additive identity for the whole numbers. 

If a is a whole number, then

$a + 0 = a = 0 + a$

For example, 

$0 + 8 = 8 = 8 + 0$.

Multiplicative Identity:

This property states that the product of a whole number and 1 results in the whole number itself. This makes 1 the multiplicative identity for whole numbers. 

If A is a whole number, then

 $a \times 1 = a = 1 \times a$. 

For example,

$23 \times 1 = 23 = 1 \times 23$.

Fun Facts!

• The closure, associative, and commutative properties do not satisfy subtraction and division in whole numbers.

• When zero is subtracted from any number, we obtain that number itself. But if we subtract any number from zero, we obtain its additive inverse.

Conclusion

In this article, we learned about what whole numbers are and looked at some of the properties that whole numbers offer over addition, subtraction, multiplication and division.

Solved Examples On Properties of Whole Numbers

1. Which of the following expressions express the multiplicative and additive identity property?

(i)   $7 \times 1 = 7$

(ii)  $0 \times 3 = 3 \times 0 = 0$

(iii) $0 + 90 = 90$

(iv) $34 \times \frac{1}{34} = 1$

Solution: 

(i)  $a \times 1 = 1 \times a = a$, where $a = 7$.

It represents multiplicative identity property.

(iv) $a + 0 = 0 + a = a$, where $a = 90$.

It represents additive identity property.

2. By using properties of whole numbers, fill in the blanks in the following expression: $165 \times 78 \times 12 = \underline{} \times 12 \times 165$

Solution:

The commutative property of multiplication states that the order of the multiplication operation does not change the product.

Thus, $165 \times 78 \times 12 = 78 \times 12 \times 165$

3. By using properties of whole numbers, fill in the blanks in the following expression: $49 + (43 + 23) = (49 + \underline{}) + 23$

Solution:

The associative property of addition states that the sum of numbers does not change regardless how we group the numbers.

Thus, $49 + (43 + 23) = (49 + 43) + 23$

4. Find the addition of $10 \times (15 + 1)$.

Solution:

By distributive property, we have

$10 \times (15 + 1) = (10 \times 15) + (101)$ 

       $= 150 + 10$

       $= 160$

Practice Problems On Properties of Whole Numbers

Frequently Asked Questions on Properties of Whole Numbers