Pythagorean Triples

Introduction to Pythagorean Triples

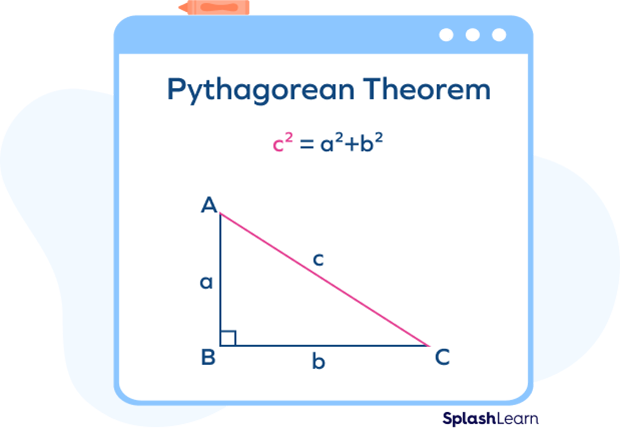
Pythagorean triples are three positive integers which satisfy the Pythagoras’ theorem. Pythagoras’ theorem states that in any right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides of the right triangle.

Any three positive integers that fully satisfy the Pythagorean theorem are known as “Pythagorean triples.” 

What Are Pythagorean Triples in Geometry?

Pythagorean triples, in simple words, are the integer solutions to the Pythagoras’ theorem, containing positive integers.

Here, “c” is the “hypotenuse” or the longest side of the triangle, and “a” and “b” are the other two sides of the right-angled triangle. We represent the Pythagorean triples as $(a, b, c)$.

The three sides a, b, c of the any right angled triangle satisfy $a^{2} + b^{2} = c^{2}$. 

So, $(a, b, c)$ form a Pythagorean triple.

Pythagorean Triples: Definition

A set of 3 positive numbers that satisfy the formula of the Pythagoras’ theorem that is expressed as $a^{2} + b^{2} = c^{2}$, where a, b, and c are positive integers, are called Pythagorean triples.

Example: $(3, 4, 5)$ is the first known, the smallest and the most popular example of Pythagorean triple. 

Let us verify if 3, 4 and 5 satisfy the equation $a^{2} + b^{2} = c^{2}$. 

$3^{2} + 4^{2} = 9 + 16 = 25 = 5^{2}$

What is the Formula for Pythagorean Triples?

For a right-angled triangle, there exists a relationship between the three sides of the triangle.

If the longest side is called the hypotenuse, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

So, we can form the formula for the Pythagoras triples as 

$a^{2} + b^{2} = h^{2}$

where 

h is the hypotenuse,

a and b are the other two sides.

Pythagorean Triples: Examples

There is an endless list of Pythagorean triples. $(3, 4, 5)$ is the first Pythagorean triple. A few more triples can be generated by multiplying all the original numbers by another positive integer.

Pythagorean Triples List

It is not possible to list down all Pythagorean triples since the list is endless. The table given below shows some examples of Pythagorean triples.

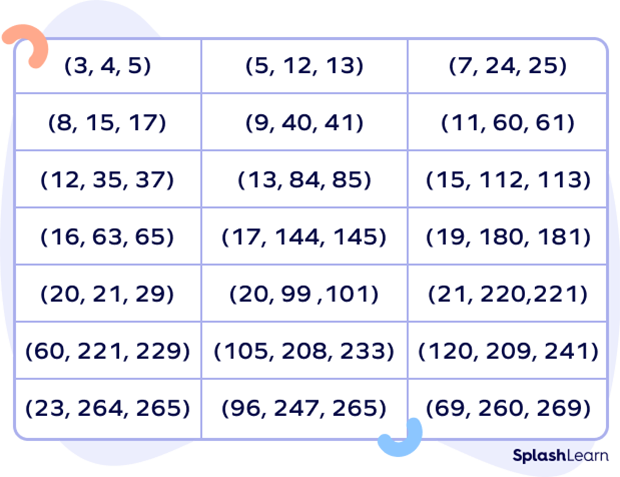
Common Pythagorean Triples

Here are a few common Pythagorean triples.

• 3-4-5
• 5-12-13
• 6-8-10
• 9-12-15
• 12-16-20

What are Primitive Pythagorean Triples?

The set of three numbers which have no common divisor other than 1 is considered to be a primitive Pythagorean triple.

The first Pythagorean triple is primitive, since 3, 4, and 5 have no common divisors other than 1. An example of an imprimitive or non-primitive Pythagorean triple is $(15, 20, 25)$ multiple of 5.

How to Find Pythagorean Triples?

Let’s understand how to find Pythagorean triples using an example.

1. Pick an even number (other than 2) to be the longer leg’s length.

So, let $b = 4$

2. Find a prime number one greater than that even number, to be the hypotenuse. 

So, hypotenuse $= h = 4 + 1 = 5$

3. Calculate the third value to find the Pythagorean triple.

          We know that, $a^{2} + b^{2}  = h^{2}$

Thus,  $a^{2} + 4^{2} = 5^{2}$

$a^{2} = 25 − 16 = 9$

$a = 3$

Pythagorean triple $= (3, 4, 5)$

Formula for Generating Pythagorean Triples

To find the Pythagorean triples, the following formula can also be used. If a, b are two sides of the right triangle and c is the hypotenuse, then

$a = m^{2} − n^{2}$

$b = 2 mn$

$c = m^{2} + n^{2}$

These values form sides of a right triangle or Pythagorean triple.

(i) m, n are positive integers.

(ii) $m > n$

(iii) m and n are coprime and both should not be odd numbers.

How to Form Pythagorean Triples?

Let us now see how we can find or generate Pythagorean triples using formulas.

Case 1: For odd numbers

Let ‘x’ be an odd number.

The Pythagorean triple will be: 

1. $x$
2. $\frac{x^{2}}{2} − 0.5$
3. $\frac{x^{2}}{2} + 0.5$.

Let us take an example: (3, 4, 5). Now, let us see how to form this Pythagorean triple.

Here,  $x = 3$, which is an odd number.

$\frac{x^{2}}{2} − 0.5 = \frac{9}{2} − 0.5 = 4.5 − 0.5 = 4$

$\frac{x^{2}}{2} + 0.5 = \frac{9}{2} + 0.5 = 4.5 + 0.5 = 5$

Hence, the Pythagorean triple formed is $(3, 4, 5)$.

Case 2: For even numbers

If “x” is an even number, then the Pythagorean triple is given as

1. $x^{2}$, 
2. $\frac{x^{2}}{2} − 1$, 
3. $\frac{x^{2}}{2} + 1$.

Let us take an example, (16, 63, 65). Now, we will check how to form the Pythagorean triple.

Here, $x = 16$, which is an even number.

$\frac{x^{2}}{2} − 1 = \frac{16^{2}}{2} − 1 = 82 − 1 = 64 − 1 = 63$

$\frac{x^{2}}{2} +1 = \frac{16^{2}}{2} + 1 = 82 + 1 = 64 + 1 = 65$.

Hence, we get the Pythagorean triple $(16, 63, 65)$

Pythagorean Triples Formula: Proof

Consider a square shown below with side (a+b).

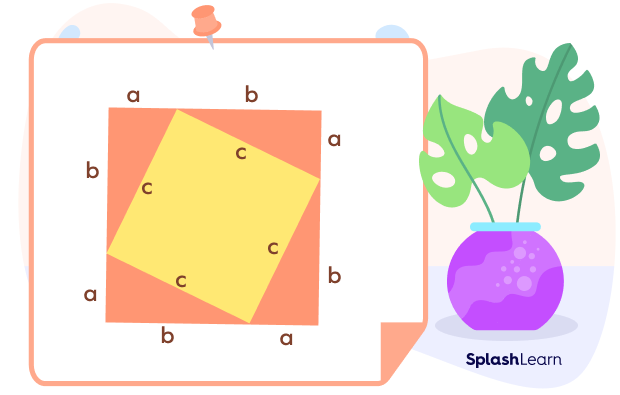
Area of the given square $= (a + b)^{2}$

Area of each small right triangle $= \frac{1}{2} ab$

Area of 4 right triangles $= 4 \times \frac{1}{2} ab = 2ab$

Area of the yellow square formed inside $= side^{2} = c^{2}$

Here, area of the whole square $=$ Area of 4 right triangles $+$ Area of Yellow square

$(a + b)^{2} = 2ab + c^{2}$

$a^{2} + 2ab + b^{2} = 2ab+ c^{2}$

$a^{2} + b^{2} = c^{2}$

Hence proved.

What are Triangular Numbers?

A triangular number or triangle number is used to count objects arranged in an equilateral triangle. A triangular number is a number that can be written as the sum of the first n positive integers. 

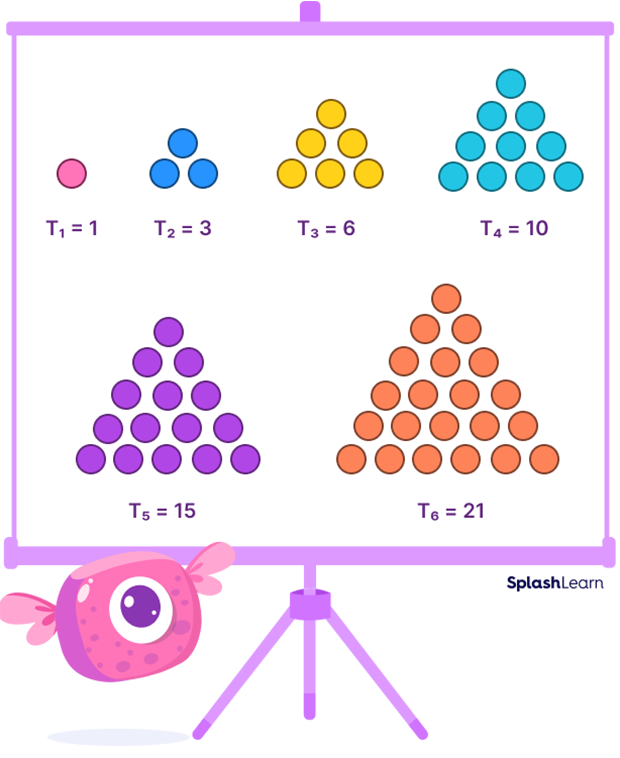
The $n^{th}$ triangular number is the sum of the n natural numbers from 1 to n. The sequence of triangular numbers, starting with the 0th triangular number, is 

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66 and so on.

Each perfect square is the sum of two successive triangular numbers.

$0 + 1 = 1$

$1 + 3 = 4$

$3 + 6 = 9$

$6 + 10 = 16$; and so on.

Fun Facts!

• The 5 most common Pythagorean triples are $(3, 4, 5), (5, 12, 13), (6, 8, 10), (9, 12, 15)$, and $(15, 20, 25)$.
• Pythagorean triples contain either all even numbers or two odd numbers and an even number. 
• A Pythagorean triple never be made up of all odd numbers or two even numbers and an odd number.

Conclusion

In this article, we learned what Pythagorean triples are. We saw many examples of Pythagorean triples and learnt the formula to find them. We also learned about triangular numbers and saw some facts about Pythagorean triples. Now let us solve some practice problems to understand the above concepts well. 

Solved Examples

1. For the Pythagorean triple (p, 15, 17) , what is the value of p?

Solution: 

Using the Pythagoras’ theorem formula, let us substitute the values in the equation: $a^{2} + b^{2} =c^{2}$, where, $a = p, b = 15, c = 17$. (Since the hypotenuse is the longest side, we have taken $c = 17)$

$c^{2} = a^{2} +b^{2}$

$17^{2} = p^{2} +15^{2}$

$289= p^{2} + 225$

$p^{2} = 64$

$p = 8$

Therefore, the value of $p = 8$

2. Does (5, 12, 13) satisfy the Pythagorean theorem? Is it a Pythagorean triple?

Solution: 

Using the Pythagoras’ theorem formula, let us substitute the values in the equation: $c^{2} = a^{2} +b^{2}$ , where, $a = 5, b = 12, c = 13$. (Since hypotenuse is the longest side, we have taken $c = 13)$

$c^{2} = a^{2} +b^{2}$

$13^{2} = 5^{2} +12^{2}$

$169 = 25 + 144$

$169 = 169$

Hence, (5, 12, 13) satisfies the Pythagorean theorem.

Therefore it is a Pythagorean triple.

3. Check if (4, 5, 6) is a Pythagorean triple.

Solution: 

Using the Pythagoras’ theorem formula, let us substitute the values in the equation: $c^{2} = a^{2} +b^{2}$ , where $a = 4, b = 5, c = 6$. (Since hypotenuse is the longest side, we have taken $c = 6)$

$c^{2} = a^{2} +b^{2}$

$6^{2} =4^{2} +5^{2}$

$c^{2} = a^{2} +b^{2}$

$36 \neq 41$

Hence $(4, 5, 6)$ is not a Pythagorean triple.

4. Find the two numbers in a Pythagorean triple if one number is 9.

Solution: First, we need to check if the given number is odd or even.

Here, 9 is an odd number. 

Hence the other two numbers in the triple will be:

$\frac{x^{2}}{2} − 0.5 = \frac{81}{2} − 0.5 = 40.5 − 0.5 = 40$

$\frac{x^{2}}{2} + 0.5 = \frac{81}{2} + 0.5 = 40.5 + 0.5 = 41$

Hence the triple $(9, 40, 41)$ will be formed.

5. Is 9-12-15 a Pythagorean triple?

Solution: 

$15^{2} = 225$

$12^{2} + 9^{2} = 144 + 81 = 225$

Thus, $12^{2} +9^{2} = 15^{2}$

The given three integers satisfy the Pythagoras’ theorem formula.

So, it is a Pythagorean triple.

Practice Problems

Frequently Asked Questions

Related Articles

• Right Angled Triangle
• Acute Angle
• Formula
• Geometry