Radicand: Definition, Symbol, Examples, FAQs, Practice Problems

What Is a Radicand in Math?

A radicand is the number or expression that appears under the radical symbol (√ ). The radicand can be any real number, positive or negative, or it can also be an algebraic expression.

The radical symbol (√ ) is used to denote the square root or the n^th roots.  In other words, the meaning of radicand is the value or quantity that you want to find the square root or the n^th root of. This definition helps to identify the radicand when the radical sign is not mentioned.

Radicand examples:

Expression	Radicand
$\sqrt{25}$	25
$\sqrt{ab}$	ab
$^{4}\sqrt{120}$	120
$^{3}\sqrt{8}$	8
$\sqrt{x + 6}$	x + 6
$^{3}\sqrt{\;-\;8}$	-8
What is the fifth root of 32? (Here, we need to find $^{5}\sqrt{32}$.)	32

The term “radicand” is commonly used in mathematics when dealing with radicals and their operations, such as square roots, cube roots, and higher roots. It helps identify or address the number or expression that is being operated on by the radical symbol.

Radicand: Definition

A radicand is part of the radicle written under the root or radical symbol. It is the value or expression being operated on.

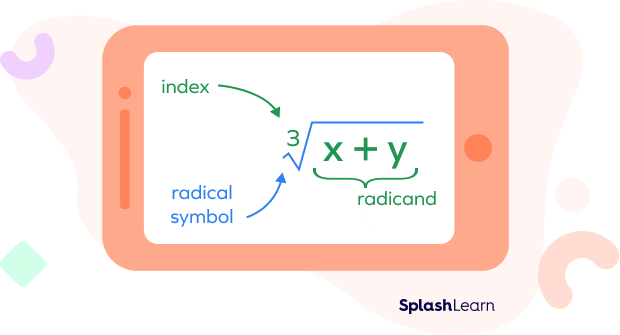
Radicand and Index

Index or index number is a small number present on the top left of the radical symbol. It specifies the type of root being taken. If the index is not mentioned, it is assumed to be 2, indicating a square root. The index value should be a positive integer greater than or equal to 2.

For example, in the expression  $^{3}\sqrt{27}$, the index is 3. 

In the expression$\sqrt{5}$, there is no index value written. In this case, the index value is assumed to be 2. 

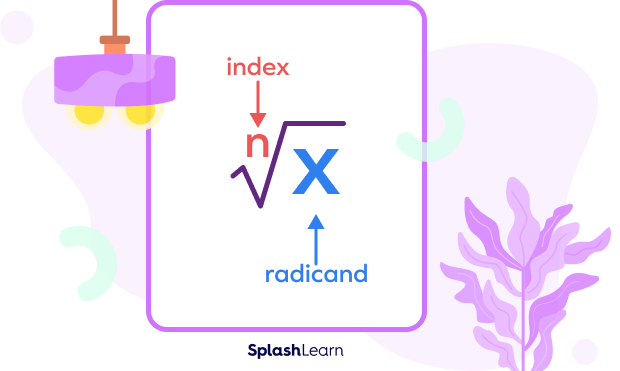
Radicand, Radical Symbol, and Radical Expression

Radical symbol: A radical is a mathematical symbol that is used to denote the square root or the n^th root of a number. Radicand sign is represented as √ or $\sqrt{}$. 

Radicand: As mentioned earlier, the radicand is the expression, or a number that appears under the radical symbol.

Radical Expression: Radical expressions, also known as radicals, are the expressions involving square roots or n^th roots. These expressions involve at least one value within a radical sign. The radicand and the radical symbol together form a radical expression.

General Rules with Radicands

• $^{n}\sqrt{a \times b} = ^{n}\sqrt{a} \times ^{n}\sqrt{b}$

• $^{n}\sqrt{\frac{a}{b}} = \frac{^{n}\sqrt{a}}{^{n}\sqrt{b}}$

• $^{n}\sqrt{a} = a^{\frac{1}{n}}$

• $^{n}\sqrt{a^{m}} = a^{\frac{m}{n}}$

• If $x^{n} = a$, then $^{n} \sqrt{a} = x$.

For example, $2 \times 2 \times 2 = 2^{3} = 8$, then $^{3}\sqrt{8} = 2$.

Positive and Negative Radicands

We generally deal with positive radicand values, however, radicands can also be negative.

If the index is even, then we must consider only positive radicands in order to get real solutions.

Here are a few examples to understand this.

Example 1: In some cases, it is not difficult to solve a cube root with negative value under the root sign. It is because a negative value multiplied with itself three times gives a negative answer.

$^{3}\sqrt{-27} = (\;-\;3)$ since $(\;-\;3) \times (\;-\;3) \times (\;-\;3) = (\;-\;27)$

Example 2: It is not possible to get a real solution if the index is even and the radicand is negative, since a negative number multiplied with itself an even number of times will never give a negative result.

$\sqrt{\;-\;4} =$ ? 

We know that 

$2 \times 2 = 4$ …the root cannot be 2!

$(\;-\;2)(\;-\;2) = 4$ …the root cannot be -2!

​​The square root of a negative number does not exist among the set of real numbers. To address such problems, we have to study imaginary numbers or complex numbers.

Can a Radicand Be a Fraction?

Yes, a radicand can be a fraction. 

Example 1: $^{3}\sqrt{\frac{2}{3}}$ , in this expression, the radicand is $\frac{2}{3}$ and the index is 3.

In some cases, we can simplify the radicand, which is in fraction form, using the formula 

$\sqrt{\frac{a}{b}} = \sqrt{\frac{a}{b}}$

Example 2:  $\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}}$

$\sqrt{\frac{4}{9}} = \frac{\sqrt{2 \times 2}}{\sqrt{3 \times 3}}$

$\sqrt{\frac{4}{9}} = \frac{3}{2}$

Facts on Radicand

Conclusion

In this article, we learned about the concept of radicand in math, definition, and examples to understand the parts of a radical expression, such as radicand, index, radical symbol, etc. Let’s solve a few examples and practice problems for better understanding.

Solved Examples on Radicand

1. From the given expression, identify the radicand: $^{3}\sqrt{8} + 27\;-\;b$.

Solution:

Given expression:  $^{3}\sqrt{8} + 27\;-\;b$

$^{3}\sqrt{8}$  is the only term that involves a radical symbol.

8 is the number written under the radical symbol.

Thus, 8 is the radicand in the given expression.

2. Simplify the given expression: $\sqrt{128} \times \sqrt{32}$.

Solution:

By applying  $\frac{x} \times \sqrt{y} = \sqrt{x \times y}$

$\sqrt{128} \times \sqrt{32} =  \sqrt{128 \times 32}$

$\sqrt{128 \times 32} =  \sqrt{4096}$

$\sqrt{128 \times 32} = \sqrt{64 \times 64}$

$\sqrt{128} \times \sqrt{32} = 64$

3. Identify the radicand and index in the expression $^{8}\sqrt{13^{2}}$.

Solution: 

Given expression: $^{8}\sqrt{13^{2}}$

$^{8}\sqrt{13^{2}}$  can also be written as $^{8}\sqrt{16^{9}}$  because $13^{2} = 169$.

The index is the number written on the top left of the radical sign, which is 8.

The radicand is the number written inside the radical symbol, which is $13^{2} = 169$.

Practice Problems on Radicand

Frequently Asked Questions about Radicand