Rate Definition in Math – Unit Rate, Ratio, Examples, Facts, FAQs

What Is Rate in Math?

A rate is a way of comparing two related quantities that are measured in different units. It tells us how much of one thing is happening in relation to another. 

Example: If you are driving a car and you want to know how fast you are going, you can look at your speedometer, which measures your speed in miles per hour (mph). The rate tells you how many miles you are driving in one hour. 

Rates are used in many everyday situations, like measuring how much you save per week or how many points you score in a game per minute. 

In ratios, we use the word “to” for comparison, while in rates, we use the word “per” to indicate the comparison between two quantities with different units. The use of “per” or “/” symbol in rate problems helps to represent the amount of one quantity in relation to another quantity with distinct units. 

Example: Robert’s typing rate is 100 words per minute. It means that he can type 100 words in one minute. Here, words and minutes are two different units being compared.

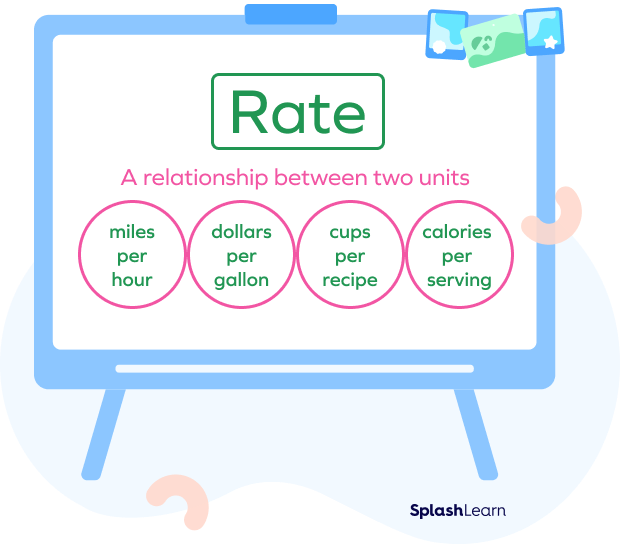
Rate Definition In Math

In mathematics, a rate is a comparison between two quantities with different units, expressed as a ratio representing the amount of one quantity per unit of another. Rate can be defined as a ratio that expresses the comparison of two different quantities which have different units.

Common examples of rate:

• Speed: Miles per hour (mph) when driving a car.
• Price: Dollars per gallon ($\$$/gal) for gasoline at the pump.
• Cooking: Cups per recipe for ingredients like flour or sugar.
• Exercise: Calories burned per minute during a workout.
• Sports: Points scored per game in basketball or touchdowns in football.

How to Find Rate

Rate involves comparing two connected quantities, with the second one often being time (such as per second or per hour) but not limited to it. It can be expressed as “this per that” or as a single value obtained through division. 

The unit of rate depends on the quantities being compared. For example, if you’re measuring speed in miles per hour, the unit would be “miles per hour.” Similarly, for a consumption rate of water, it could be “liters per minute.” The unit of rate provides context and helps understand the comparison between different quantities.

Usually, the rate formula is derived as the ratio of two different quantities with different units. Thus, it can be written as :

Rate $= \frac{Quantity\;1}{Quantity\;2}$

To calculate the rate of quantities, follow the steps given below:

Step 1: Write two quantities with different units.

Step 2: Calculate the ratio of quantity 1 to quantity 2.

Step 3: To find the rate, the ratio should be simplified to its simplest form.

Step 4: Write the answer in $\frac{Unit\;1}{Unit\;2}$ form.

Example: John traveled in a car for 3 hours and reached 27 miles. To calculate the rate of speed let us use the formula: Rate $= \frac{Quantity\;1}{Quantity\;2}$

Quantity 1 = 27 miles

Quantity 2 = 3 hours

Substituting both values in the formula,

Rate $= \frac{27}{3} = 9$.

Thus, the speed of the car is the rate which is 9 miles/hour or 9 miles per hour.

What Is Unit Rate?

Unit rate is a way to compare how much of something happens or is used in relation to one unit of something else. It helps us understand how things change for every single unit of something else. 

Unit rate is also a comparison between two quantities of different units; however, the quantity of the denominator is always 1.

Example: If you’re driving at a speed of 60 miles per hour, the unit rate is 60 miles traveled for every 1 hour passed. 

Unit Rate Definition in Math

In mathematics, a unit rate refers to the measurement of a single unit of one quantity in relation to another quantity. It’s often expressed as a ratio, where the numerator represents the amount of the first quantity and the denominator represents the corresponding amount of the second quantity. 

The concept of a unit rate sets it apart from a general rate, as it involves comparing a specific number of units from the first quantity to a single unit from the second quantity. Essentially, the second quantity in the comparison is fixed at 1. 

It is a certain number of units of the first quantity that is compared to 1 unit of the second quantity. When these quantities are put in ratio, the unit rate is found. Unit rates are used to compare values with different units and help understand how they relate to each other in a standardized way.

Example: Imagine driving a car that covers a distance of 300 miles using 15 gallons of gasoline. In this scenario, the unit rate can be calculated as “20 miles per gallon,” indicating that for every gallon of gasoline, the car can travel 20 miles.

How to Find Unit Rate

To find the unit rate, divide the quantity being measured by the unit of reference. In a unit rate, the second quantity is always 1. To find the unit rate, divide the top number by the bottom number so that the bottom number becomes 1.

This will help you determine how much of the quantity corresponds to one unit of the reference. For example, if you traveled 240 miles in 4 hours, the unit rate would be 60 miles per hour.

Usually, the unit rate formula is derived as the ratio of the first quantity to one unit of the second quantity. 

Difference Between Rate and Ratio

Rate	Ratio
Rate is the comparison of different units.	Ratio is the comparison of the same units.
It is expressed by the word ‘per’ or the symbol ‘/’.	It is expressed by the word ‘to’ or the symbol ‘:’.
Example: 200 miles per hour or 200 miles/hour.	Example: 5 cups of sugar to 2 cups of milk or expresses as 5:2

Facts about Rate

Conclusion

In this article, we learned about rates and how they help us compare different quantities with varying units. Understanding rates is crucial for various real-world scenarios. Now, let’s solidify our understanding by exploring examples and practicing multiple-choice questions to enhance our comprehension.

Solved Examples on Rate

Example 1: Find the unit rate if the printer can print 50 pages in 10 seconds.

Solution:

The number of pages printed in 10 seconds = 50 pages

So, number of pages in 1 second $= \frac{50}{10} = 5$ pages.

The unit rate is 5 pages per second.

Example 2: What is the speed of the train if it has traveled 240 miles in 12 hours?

Solution:

Train traveled in 12 hours = 240 miles

Train traveled in one hour $= \frac{240}{12}$ miles = 20 miles.

The speed of the train is 20 miles per hour.

Example 3: What is the rate of cake baking per hour, if 40 cakes are baked over the course of 8 hours?

Solution:

Number of cakes baked in 8 hours = 40 cakes

Number of baked in one hour $= \frac{40}{8}$ cakes. = 5 cakes

So, the average number of cakes baked in an hour is 5 cakes per hour.

Practice Problems on Rate

Frequently Asked Questions about Rate