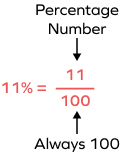Ratio to Percentage Conversion – Steps, Formula, Table, Examples, FAQs

What Is the Ratio to Percentage Conversion?

The ratio to percentage conversion refers to the method of converting any given ratio into its equivalent percentage value.

Two quantities of the same kind and same unit are compared using the ratio. So, a ratio tells us how much of one quantity is present in relation to another quantity. For example, if the water to milk ratio is 1:2, it means that for 1 glass of water, you must add 2 glasses of milk.

 A percentage, on the other hand, is a particular kind of ratio where the value of the denominator is always equal to 100. For example, $25\%$ means $\frac{25}{100}$.

How to Convert Ratio to Percentage 

Let’s understand how to express a ratio as a percentage.

Step 1: Write the ratio a:b in the fraction form $\frac{a}{b}$.

Step 2: Multiply $\frac{a}{b}$ by 100.

Step 3: Add the percentage sign $(\%)$ to the resultant value.

Example 1: Convert the ratio 3 : 5 into percentage.

The ratio 3 : 5 is written in the fraction form as $\frac{3}{5}$.

Multiply $\frac{3}{5}$ by 100.

 $\frac{3}{5} \times 100 = 60$

Adding the percentage symbol $(\%)$ to the resultant value, we get $60\%$.

The ratio 3 : 5 in percentage form is $60\%$.

In certain examples, identifying the ratio can be tricky. Let’s see one such example.

Example 2: The ratio of blue pens to red pens in a box is 1 : 4. What is the percentage of blue pens present in the box?

The ratio of pens to pencils $= 1 : 4$

It means that if there are $1 + 4 = 5$ items in the box, there will be 1 blue pen and 4 red pens.

Ratio of blue pens to the total number of items $= 1 : 5$

Ratio to percentage $= \frac{1}{5} \times 100 = 20\%$

Percentage of blue pens in the box $= 20\%$

Ratio to Percentage Formula

The formula for converting ratios to percentages is as follows:

Percentage $=$ Ratio $\times 100$ 

Add the sign $\%$ is used to denote the percentage.

Example:  $5 : 10 =  \frac{5}{10} \times 100 = 50\%$

Ratio to Percentage Table

Ratio	Percentage Conversion	Percentage
1: 2	$\frac{1}{2} \times 100$	$50\%$
1: 3	$\frac{1}{3} \times 100$	$33.33\%$
1: 4	$\frac{1}{4} \times 100$	$25\%$
1: 5	$\frac{1}{5} \times 100$	$20\%$
1: 10	$\frac{1}{10} \times 100$	$10\%$
2: 5	$\frac{2}{5} \times 100$	$40\%$
1: 25	$\frac{1}{25} \times 100$	$4\%$
4: 5	$\frac{4}{5} \times 100$	$80\%$
1: 50	$\frac{1}{50} \times 100$	$2\%$
1: 100	$\frac{1}{100} \times 100$	$1\%$

Facts about Ratio to Percentage Conversion

Conclusion

In this article, we learned how to convert a ratio to a percentage, formula, and steps. Let’s solve a few examples and practice problems to revise the concept.

Solved Examples on Fractions to Percentage Conversion

1. Convert 4 : 5 ratio into percentage.

Solution: 

Given ratio $= 4 : 5$

The ratio 4 : 5 is written as $\frac{4}{5}$.

Multiplying  $\frac{4}{5}$ by 100. Add $\%$ sign to the result.

 $\frac{4}{5} \times 100 = 80\%$

2. The ratio of Monica’s expenses and savings is 8 : 2. What percentage of her income did she spend, and what percent did she save?

Solution: 

Expenses to savings ratio $= 8 : 2$

Total parts $= 2 + 8 = 10$

 This suggests that $\frac{8}{10}$ of the salary is spent, and only $\frac{2}{10}$ is saved.

Converting ratio to percentage we get,

Percentage of expenditure $= \frac{8}{10} \times 100 = 80\%$

Similarly, percentage of savings $= \frac{2}{10} \times 100 = 20\%$

3. On a canvas, the ratio of the red and black is 2 : 3. What percentage of red color is used?

Solution: 

Total number of  parts $= 2 + 3 = 5$

$\frac{2}{5}$ parts are filled in red.

Percentage of red color $= \frac{2}{5} \times 100 = 40\%$

35 parts are filled in black.

Percentage of black color $= \frac{3}{5} \times 100 = 60\%$

Practice Problems on Ratio to Percentage Conversion

Frequently Asked Questions on Ratio to Percentage Conversion