What is a Reciprocal in Math?
The word “reciprocal’ comes from the Latin word “reciproc(us)”, meaning “returning” or “alternating.”
So, what is the meaning of reciprocal in math? How to find the reciprocal of a number? Simply divide 1 by the given number. In other words, we turn the number upside down, or interchange the numerator and denominator.
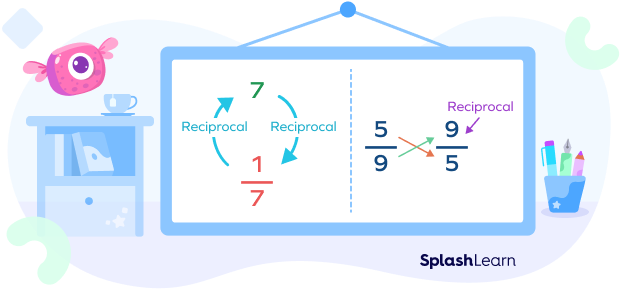
Definition of Reciprocal in Math
In math, the reciprocal of any quantity can be defined as 1 divided by that quantity.
How To Find Reciprocal
For any non-zero number “x,” the reciprocal will be $\frac{1}{x}$.
If we multiply the given number by its reciprocal, we get the product 1.
The reciprocal of x is also represented by $x^{-1}$.
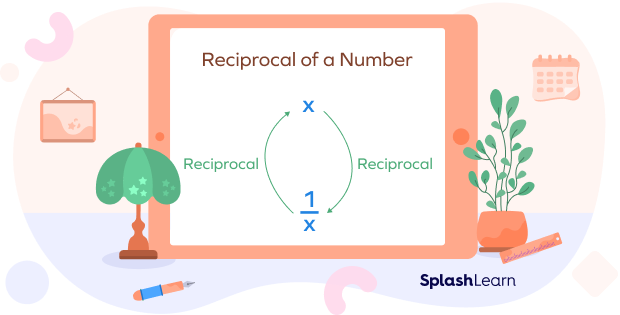
Rules of Reciprocals
Let’s discuss two reciprocal rules.
- For a number x, the reciprocal will be $\frac{1}{x}$ and it can also can be written as $x^{-1}$.
For example, if 10 is the number, then the reciprocal will be $\frac{1}{10}$.
- For a fraction $\frac{x}{y}$, the reciprocal will be $\frac{y}{x}$.
For example, the reciprocal of $\frac{2}{7}$ is $\frac{7}{2}$.
What Is the Reciprocal of Zero?
We can find the reciprocal of any number, but we cannot apply the reciprocal condition on zero, since it will give an indefinite value. Division of any number by 0 is undefined.
Thus, we can have a reciprocal for all real numbers except 0.
Reciprocal of a Natural Number
The reciprocal of a natural number is defined as the one divided by the given number.
Suppose we have to find the reciprocal of 5.
We know that reciprocal of a number x is $\frac{1}{x}$.
Therefore, reciprocal of a 5 is $\frac{1}{5}$.
Reciprocal of Negative Numbers
For any negative number $(\;-\;x)$, we can find the reciprocal by writing the inverse of the given number with a minus sign along, $-\frac{1}{x}$.
Suppose we have to find the reciprocal of $-\;8$, we follow the steps given below:
Step 1: We write the given number in the form of an improper fraction by writing the number 1 in the denominator. So, 8 can be written as $\frac{8}{1}$.
Step 2: Interchange the numerator and denominator values. On interchanging in the example, we get 18.
Step 3: Add a minus sign $( \;–\; )$ to the resultant number. We get $-\;\frac{1}{8}$.
Reciprocal of a Fraction
The reciprocal of a fraction is obtained by interchanging the numerator and the denominator.
Suppose we have to find the reciprocal of $\frac{4}{5}$.
Use the formula, reciprocal of $x = \frac{1}{x}$,
Here, $x = \frac{4}{5}$
Thus, $\frac{1}{x} = \frac{1}{\frac{4}{5}} = \frac{5}{4}$
Therefore, the reciprocal of a fraction $\frac{4}{5}$ is $\frac{5}{4}$.
Reciprocal of a Mixed Fraction
Suppose we have a mixed fraction $5\frac{1}{3}$.
Step 1: Convert the mixed fraction into an improper fraction.
In this case, we get $\frac{16}{3}$.
Step 2: Flip the numerator and denominator.
In this case, we get $\frac{3}{16}$.
Thus, the reciprocal of $5\frac{1}{3}$ is $\frac{3}{16}$.
Reciprocal of a Decimal
We calculate the reciprocal of a decimal by one over the decimal number.
Method 1:
Suppose we have to find a reciprocal of 0.25.
Step 1: Flip the numerator and the denominator.
In this case, we get $\frac{1}{0.25}$.
Step 2: Change it to fractional form.
In this case, we get $\frac{100}{25} = 4$
Step 3: If we get a whole number, we leave it till Step 2. If we get a fraction, we convert it into decimal by dividing the numerator by denominator.
Method 2:
Suppose we have to find the reciprocal of 0.52.
Step 1: Check whether the given decimal number is possible to convert into a fractional number. Here 0.52 is written as $\frac{52}{100} = \frac{13}{25}$.
Step 2: Find the reciprocal of the fraction. Here, we get $\frac{25}{13}$.
Step 3: Convert the fraction into decimals. Here, we get 1.92.
Unity: Product of a Number and Its Reciprocal
If we multiply the number by the reciprocal of the number, we will get unity, that is, 1.
Some examples are given below:
- $5\times\frac{1}{5} = 1$
- $\frac{2}{3}\times\frac{3}{2} = 1$
- $50\times\frac{1}{50} = 1$
- $\frac{9}{10}\times\frac{10}{9} = 1$
Applications of Reciprocal
The most important application of reciprocal is that it is used in division operation for fractions. If we want to divide the one fraction by the second fraction, we can find it by multiplying the first fraction with the reciprocal of the second fraction.
Suppose we have to find $\frac{1}{5}\div\frac{7}{5}$.
Here, the first fraction is $\frac{1}{5}$.
The second fraction is $\frac{7}{5}$.
Thus, the reciprocal of the second fraction is $\frac{5}{7}$.
Hence, $\frac{1}{5}\div\frac{7}{5} = \frac{1}{5}\times\frac{5}{7}= \frac{1}{7}$.
Facts about Reciprocal
- Reciprocal of a number is also called its multiplicative inverse.
- Reciprocal of a number is 1 divided by the number.
Solved Examples on Reciprocal
1. What is the reciprocal of 7?
Solution: The reciprocal of 7 is $\frac{1}{7}$.
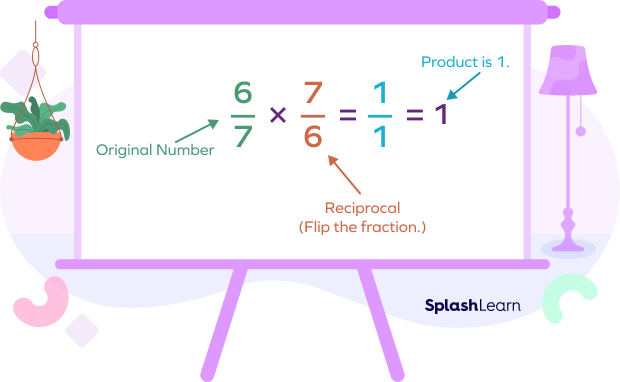
2. What is the reciprocal of $\frac{6}{7}$? Verify your answer.
Solution: The reciprocal of a fraction $\frac{x}{y}$ is $\frac{y}{x}$. So, reciprocal of $\frac{6}{7}$ is $\frac{7}{6}$.
Also, $\frac{6}{7}\times\frac{7}{6} = 1$. Hence, verified.
3. What is the reciprocal of $\frac{5x}{3}$?
Solution:
Reciprocal of $\frac{5x}{3}$ is $\frac{3}{5x}$.
4. A pizza is sliced into 8 pieces. Tom eats 3 slices of the pizza and leaves the rest. Determine the reciprocal of the quantity of the pizza left by Tom.
Solution:
Total number of slices $= 8$
Number of slices Tom ate $= 3$
Number of slices left $= 8 \;–\; 3 = 5$
Fraction of pizza left by Tom $= \frac{5}{8}$
Reciprocal $= \frac{8}{5}$
5. Stuart bought 4 apples from the market. He ate $2\frac{1}{2}$ apples from the 4 he bought. Determine the reciprocal of the fraction of the apples he ate.
Solution: Fraction of the apples he ate $= 2\frac{1}{2} = \frac{5}{2}$
Reciprocal $= \frac{2}{5}$
Practice Problems On Reciprocal
Reciprocal: Definition, Rules, Solved Examples, Facts, FAQs
Which of the following statements is false?
Reciprocal of $–\; 15$ is $\;-\;\frac{1}{15}$.
The reciprocal of 0 is ______.
The reciprocal of 0 is not defined.
Which of the following is the reciprocal of $21\times5$?
Reciprocal of 21 is $\frac{1}{21}$ and reciprocal of 5 is $\frac{1}{5}$. So, reciprocal of $21\times5$ is $\frac{1}{21\times5}$.
Identify the reciprocal of 0.075 from the following options.
$0.075 = \frac{75}{1000} = \frac{3}{40}$ Reciprocal of $\frac{3}{40}$ is $\frac{40}{3} = 13.3$
If the reciprocal of an algebraic expression is $2x^2y$, then the expression will be _______________.
Reciprocal of $2x^2y$ is $\frac{1}{2x^2y}$.
Frequently Asked Questions On Reciprocal
What is the reciprocal of infinity?
The reciprocal of infinity is 0.
Which natural number has the same reciprocal as the number itself?
Reciprocal of 1 is $\frac{1}{1} = 1$. So, 1 has the same reciprocal as the number itself.
What is the difference between reciprocal and inverse?
Inverse means opposite and reciprocal means equality. A reciprocal is a type of inverse but inverse is not necessarily a reciprocal.
What is the other name of reciprocal?
The other name of reciprocal is multiplicative inverse.
What is the reciprocal of the reciprocal of a number?
The reciprocal of the reciprocal of a number is the number itself. For example: The reciprocal of 2 is $\frac{1}{2}$ and the reciprocal of $\frac{1}{2}$ is $\frac{1}{\frac{1}{2}} = 2$.
















