Relatively Prime

Relatively Prime Numbers: Introduction

We know that a prime number is a number that has only two factors, 1 and the number itself. So, what are relatively prime numbers? What does relatively prime mean? Numbers that have 1 as the only common factor are said to be relatively prime. Relatively prime numbers need not be prime numbers!

What are Relatively Prime Numbers?

When two numbers have no common factors other than 1, they are said to be relatively prime. In other words, no number other than 1 can divide them both exactly (without any remainder). 

Relatively prime numbers are also called “coprime numbers” or “mutually prime numbers.”

Two numbers m and n are said to be relatively prime if GCF(a,b) $= 1$.

In that case, the pair (a, b) is called a relatively prime pair.

Example: 5, 7 are relatively prime since GCF $(5,7) = 1$

The two numbers that are relatively prime may be prime or composite. Two composite numbers can also be relatively prime. But the common factor of both the numbers is none other than “1.”

Consider an example. What are the common factors between 9 and 25?

The only common factor of 9 and 25 is 1. 

Thus, 9 and 25 are relatively prime. 

Note that 9 and 25 are composite numbers (not prime numbers!).

Example 1: 15 and 16

Factors of 15  are 1, 3, 5 and 15.

Factors of 16 are 1, 2, 4, 8 and 16.

Common factor of 15 and 16 is only 1.

Hence, 15 and 16 are relatively prime numbers. However, 15 and 16 both are composite numbers.

Example 2: 15 and 18

Factors of 15  are 1, 3, 5 and 15.     

Factors of 18 are 1, 2, 3, 6, 9, 18.

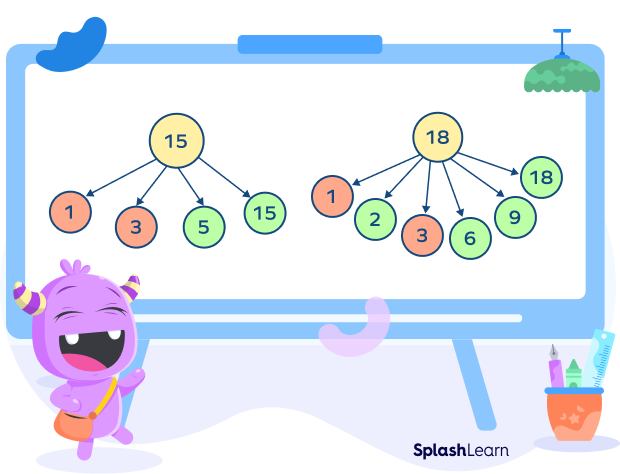
Common factors of 15 are 1 and 3.

Hence, 15 and 18 are not relatively prime numbers.

How to Find Relatively Prime Numbers

To find whether two numbers are relatively prime or not, we find the Highest Common Factor (HCF) (or Greatest Common Divisor GCD) of the given numbers.

 If the HCF is 1, then the two numbers are said to be relatively primes.

To find the HCF (Highest Common Factor) of two numbers, we first list all the factors and then identify the highest common factor out of those.

Example 1: 11 and 12

The factors of 11 are 1 and 11.

The factors of 12 are 1, 2, 3, 4, 6 and 12.

Here, 1 is the only common factor of 11 and 12.

HCF of $(11, 12) = 1,$

Thus, (11, 12) is relatively prime because only 1 is a common factor.

Example 2: 14 and 16

The factors of 14 are 1, 2, 7, and 14.

The factors of 16 are 1, 2, 4, 8 and 16

Here, 1 and 2 are the common factors of 14 and 16.

HCF $(14, 16) = 1 \times 2 = 2$

Thus, (14, 16) is not relatively prime. 

Properties of Relatively Prime Numbers

Here are a few properties of relatively prime numbers. You can easily form a “list of relatively prime numbers” using these properties.

• Any two consecutive integers are always relatively prime.

Example: (2, 3) ; (11, 12) ; (21, 22) ; (100, 101) and so on.

• Any two prime numbers are relatively prime to each other. As every prime number has only two factors 1 and the number itself, the only common factor of two prime numbers will be 1.

Example: 11 and 13 are two prime numbers. Factors of 11 are 1, 11, and factors of 13 are 1, 13. The only common factor is 1 and hence they are relatively prime.

• If two numbers have 0 and 5 at ones place, then they are not relatively prime to each other.

For example: 10 and 15 are not relatively prime since their HCF is 5 (or divisible by 5).

• The sum of two relatively prime numbers is always relatively prime with their product.

 For example, 4 and 5 are relatively prime numbers. Here, $4 + 5 = 9$ is relatively prime with $4 \times 5 = 20$. As the only common factor of 9 and 20 is 1.

• The Least Common Multiple (LCM) of two relatively prime numbers is always equal to their product.

For example: LCM of 4 and 5 (relatively prime numbers) $= 20$.

•  If n is a prime number, then all integers less than or equal to n are relatively prime to n.
•  If a and b are two relatively prime numbers, then $a + b$ is relatively prime to $a \times b$.
• If a and b are relatively prime numbers, then HCF $(a, b) = 1$ and LCM $(a, b) = a \times b$.  

Fun Facts!

• 1 is relatively prime with every number even itself.
• 0 and 1 are relatively prime numbers, as the common factor is 1.
• 0 is not relatively prime with any other integer except 1. It is divisible by any integer.
• Any two prime numbers are relatively prime.
• Any two consecutive numbers are relatively prime.
• A prime number is relatively prime with any other number if the other number is not the multiple of the given prime number.
• Two even numbers can never form a relatively prime pair as all the even numbers have a common factor as 2.
• Relatively prime numbers don’t need to be prime numbers. For example, two composite numbers 12 and 35 are relatively prime numbers because their HCF is 1.
• Relatively Prime numbers are also called “coprime” numbers or “mutually prime” numbers.
• The Least Common Multiple (LCM) of two relatively prime numbers is always equal to their product.

Conclusion

In this article, we learned that two integers are relatively prime if the common factor or the Highest Common Factor (HCF) of the two numbers is “1.” So two consecutives integers are relatively prime.  Relatively prime numbers don’t need to be prime numbers. Two composite numbers can be relatively prime.

Solved Examples 

1. Check whether 11 and 21 are relatively prime/co-prime numbers.

Solution:

Factors of 11 are 1 and 11. 

Factors of 21 are 1, 3, 7 and 21. 

They have only 1 as a common factor. Thus, 11 and 21 are relatively prime/co-prime numbers. 

2. Check whether 13 and 23 are relatively prime/co-prime numbers.

Solution: 

13 and 23 both are prime numbers. 

From the property of relatively prime numbers, numbers 13 and 23 are relatively prime numbers.

Alternatively, since 13 is a prime number, its factors are 1 and 13 only. 

And 23 is also a prime number, so its factors are 1 and 23 only.

They have only 1 as a common factor, so 13 and 23 are relatively prime/co-prime numbers. 

3. Check whether 155 and 290 are relatively prime/co-prime numbers. 

Solution:

The given two numbers are 155 and 290.

155 and 290 are divisible by 5, as the last digit of the numbers are 5 and 0 respectively. 

From the properties of relatively prime numbers, 155 and 290 are not relatively prime.

Alternatively,

$155 = 1 \times 5 \times 31$

$290 = 1 \times 2 \times 5 \times 29$

HCF $(155, 290) = 1 \times 5 = 5 \neq 1$

Therefore, 155 and 290 are not relatively prime. 

4. Check whether 200 and 201 are relatively prime/co-prime numbers.

Solution:

Numbers 200 and 201 are consecutive integers.

Hence, 200 and 201 are relatively prime/co-prime numbers. 

5. If a and b are two relatively prime numbers whose lowest common multiple is 195. If a = 15, what is the value of b?

Solution:

The Least Common Multiple (LCM) of two relatively prime numbers is always equal to their product.

So, $a \times b = 195$

 $15 \times b = 195$

 $b = \frac{195}{15}$

$b = 13$

Practice Problems

Frequently Asked Questions