What Is Sample Mean Formula?
Sample mean formula is used to calculate the sample mean, which is a statistical measure that represents the average value of a set of data points in a sample, which is basically a subset of a much larger data set (called population). It is used to estimate the population mean.
Sample mean is calculated by summing up all the data points in the sample and dividing the sum by the number of data points.
In mathematical terms, the sample mean (denoted as x) of a sample with “n” data points x₁ , x₂ , x₃ ,…, xₙ is calculated as:
Sample Mean Formula: $x = \frac{(x₁ + x₂ + x₃ + … + xₙ)}{n}$
The sample mean is commonly used to estimate the population mean by choosing a small subset of the population as a sample, especially when it is not feasible or practical to collect data from the entire population. By calculating the sample mean, we can gain insights into the central tendency or average value of the sample data.
Recommended Games
Understanding Sample Mean and Population Mean
Let’s consider a real-life situation to understand sample mean and population mean.
Imagine you want to determine the average height of all 10 year olds in the USA. The population mean would represent the true average calculated for the heights of all 10 year old kids in the USA. Here, you have to measure the height of each 10 year old kid, which is not a practical approach.
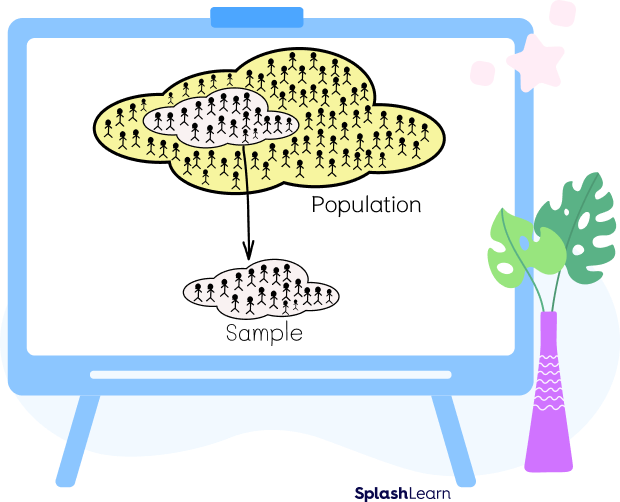
Instead, you can take a small sample of 10-year-old kids from different regions, measure their heights, and calculate the mean. This is called a sample mean, calculated by taking the average of the observations in the sample. It gives a fair estimate of the population mean.
So, using the sample mean, you can find a reasonable approximation of the average height of all 10-year-old kids in the country without actually measuring the height of every individual.
The important thing to understand is that the bigger the sample size, the more accurate your results are!
Sample Mean Formula
Let x₁, x₂, x₃, …, xₙ be the individual data points in a sample of size “n.” The sample mean, denoted as x is calculated using the formula:
$x = \frac{(x₁ + x₂ + x₃ + … + xₙ)}{n}$
This formula calculates the sum of all the data points in the sample and then divides it by the number of data points to find the average or mean value. It represents a statistical measure of the central tendency of the sample data.
How to Find Sample Mean
To find the sample mean, start with a set of data points for which you want to find the sample mean.
Step 1: Note down the values in the sample.
Let your data points be: 10, 15, 20, 25, and 30.
Step 2: Add up all the data points.
$10 + 15 + 20 + 25 + 30 = 100$.
Step 3: Count the number of data points in your sample.
In this case, there are five data points.
Step 4: Divide the sum of the data points by the number of data points to calculate the sample mean.
Sample mean$= \frac{100}{5} = 20$
So, the sample mean of the data points 10, 15, 20, 25, and 30 is 20.
Facts about Sample Mean Formula
- The sample mean is a statistical measure that represents the average value of a set of data points in a sample.
- The sample mean aims to be representative of the population mean, especially when it is not feasible to collect data from the entire population. It allows for making inferences about the larger population based on the sample data.
- The sample mean can be influenced by outliers or extreme values in the data. Outliers have a greater impact on the mean compared to other measures of central tendency, such as the median.
- The sample mean becomes more reliable and accurate as the sample size increases. A larger sample size reduces the variability and sampling error in estimating the population mean.
- Notation: The sample mean is often denoted as “x-bar” (x) to distinguish it from the population mean (μ).
- Unbiased estimator: When the sample is drawn randomly and independently from the population, the sample mean is an unbiased estimator of the population mean. This means that, on average, the sample mean is equal to the population mean.
- Statistical significance: The sample mean can be used to test hypotheses and determine statistical significance. Techniques like t-tests and ANOVA rely on comparing sample means to make inferences about population means.
- Interpretation: It is important to interpret the sample mean in the context of the data and the research question. Consider the variability, distribution, and other relevant factors to draw meaningful conclusions from the sample mean.
Solved Examples on Sample Mean
1. Consider a sample of test scores obtained by five students: 78, 85, 92, 88, and 95. Calculate the sample mean.
Solution:
To find the sample mean, we sum up all the data points and divide by the number of data points in the sample.
Sample mean $(\overline{x}) = \frac{(78 + 85 + 92 + 88 + 95)}{5}$
$= \frac{438}{5}$
$= 87.6$
2. Suppose you have a sample of the heights of six individuals in centimeters: 165, 170, 175, 162, 168, and 180. Find the sample mean.
Solution:
Sample mean $(\overline{x}) = \frac{(165 + 170 + 175 + 162 + 168 + 180)}{6}$
$= \frac{1020}{6}$
$= 170$
Hence, the sample mean of the heights is 170 centimeters.
3. You collect a sample of monthly incomes (in dollars) of eight individuals: 2500, 3000, 3500, 2800, 3200, 2900, 2600, and 2700. Determine the sample mean.
Solution:
To calculate the sample mean, we sum up all the incomes and divide by the number of data points.
Sample mean $(\overline{x}) = \frac{(2500 + 3000 + 3500 + 2800 + 3200 + 2900 + 2600 + 2700)}{8}$
$\overline{x} = \frac{23600}{8}$
$\overline{x} = 2950$
Thus, the sample mean of the incomes is $\$2950$.
4. Suppose you conduct a survey asking participants to rate their satisfaction with a new product on a scale of 1 to 5. The responses from a sample of six participants are as follows: 4, 3, 5, 2, 4, and 3. Calculate the sample mean satisfaction rating.
Solution:
To find the sample mean, sum up all the satisfaction ratings and divide by the number of participants.
Sample mean $(\overline{x}) = (4 + 3 + 5 + 2 + 4 + 3)6$
$= 216 ≈ 3.5$
5. The daily temperatures (in degrees Celsius) recorded for a week in a particular city are: 25, 27, 24, 23, 26, 28, and 29. Calculate the sample mean. What does it say about the temperature throughout the month?
Solution:
To determine the sample mean, sum up all the temperatures and divide by the number of days.
Sample mean $(\overline{x}) = \frac{(25 + 27 + 24 + 23 + 26 + 28 + 29)}{7}$
$= \frac{182}{7}$
$≈ 26\; C^{\circ}$
The temperature throughout the month will be around 26 degree celsius.
Practice Problems on Sample Mean Formula
How to Find Sample Mean: Definition, Formula, Examples
A survey asks participants to rate their satisfaction with a new restaurant on a scale of 1 to 10. The responses from a sample of seven participants are as follows: 7, 8, 9, 6, 8, 7, and 9. Find the sample mean.
Sample mean $(\overline{x}) = \frac{(7 + 8 + 9 + 6 + 8 + 7 + 9)}{7} = \frac{54}{7} ≈ 7.71$
Find the sample mean. 0.3, 0.4, 0.35, 0.38, and 0.42.
Sample mean $(\overline{x}) = \frac{(0.3 + 0.4 + 0.35 + 0.38 + 0.42)}{5} = \frac{1.85}{5} = 0.37$
The bigger the ________, the more accurate is the estimate of the population mean.
The bigger the sample size, the more accurate is the estimate of the population mean.
Cato’s daily expenses are: $\$1000,\; \$1200,\; \$900$, and $\$1100$. Estimate his weekly expenses.
Sample mean $= \frac{(1000 + 1200 + 900 + 1100)}{4} = \frac{4200}{4} = 1050$
Estimate of weekly expenses $= \$1050 \times 7 = \$7350$
Frequently Asked Questions about Sample Mean Formula
What is the purpose of calculating the sample mean?
The sample mean is calculated to estimate the average or central tendency of a sample. It is often used to estimate the population mean when it is not feasible to collect data from the entire population.
How is the sample mean different from the population mean?
The sample mean represents the average value of a sample, while the population mean represents the average value of an entire population. The sample mean is used as an estimate of the population mean, providing insights into the larger population based on the sampled data.
Can outliers affect the sample mean?
Yes, outliers can have a significant impact on the sample mean. Outliers are extreme values that deviate greatly from the other data points. Due to their large magnitude, outliers can skew the sample mean toward higher or lower values, making it less representative of the overall data.
Is the sample mean always an unbiased estimator of the population mean?
No, the sample mean is not always an unbiased estimator of the population mean. However, when the sample is drawn randomly and independently from the population, the sample mean is an unbiased estimator, meaning that, on average, it is equal to the population mean.
How does sample size affect the sample mean?
Sample size plays a crucial role in determining the reliability and accuracy of the sample mean. A larger sample size reduces the variability and sampling error, resulting in a more precise estimate of the population mean. With a larger sample size, the sample mean tends to be closer to the population mean.

















