What Is SAS Theorem (Side-Angle-Side Theorem) in Geometry?
The SAS theorem, which stands for Side-Angle-Side theorem, is a criterion used to prove triangle congruence and also triangle similarity. However, the terms or the conditions of the SAS theorem for triangle congruence and triangle similarity are slightly different.
Congruent Triangles: Two triangles are said to be congruent if they have the same shape and the same size. Corresponding angles and corresponding sides of two congruent triangles are also congruent. The triangle congruence is denoted using the symbol ≅.
Similar Triangles: Two triangles are said to be similar if they have the same shape but different sizes. Corresponding angles of similar triangles are congruent. Corresponding sides of two similar triangles are proportional. We denote the triangle similarity using the symbol .
The SAS theorem helps to prove the triangle congruence (or similarity) based on the lengths of any two sides and the measurement of the included angle between these sides.
SAS Definition in Geometry
SAS Congruence Theorem: When the two sides of a triangle are equal to the two sides of another triangle, and the angles formed by these sides (the included angles) are also equal, then the two triangles are congruent.

SAS Similarity Criterion: If two sides of a triangle are proportional with two sides of another triangle, and if the corresponding included angles formed by these sides are congruent, then the two triangles are similar.
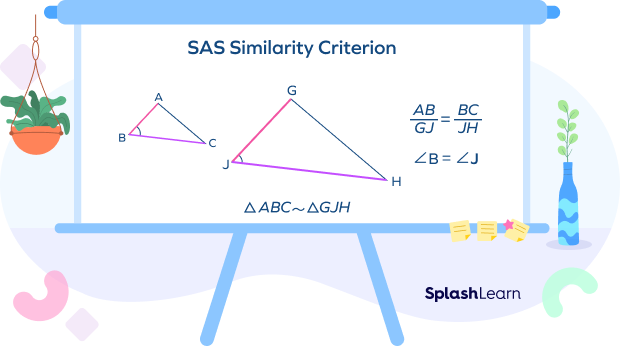
SAS (Side-Angle-Side) Congruence Theorem
SAS congruence theorem states that, if two sides and the included angle of one triangle are congruent to the two sides and the included angle of another triangle, then the triangles are congruent.
SSS Congruence Theorem Example:
Are the given two triangles congruent?
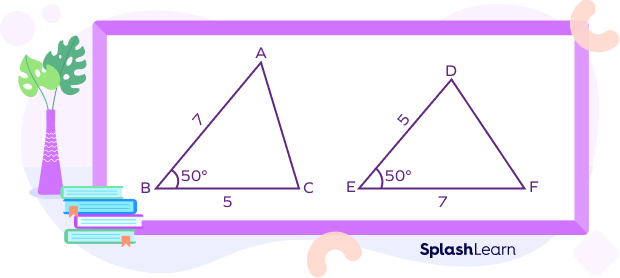
AB= EF = 7 units
BC = DE = 5 units
∠B= ∠E = $50^{\circ}$
Thus, ΔABC ≅ ΔFED by SAS congruence theorem
SAS (Side-Angle-Side) Similarity Rule
SAS congruence theorem states that, if two sides of one triangle are proportional to the corresponding sides of another triangle, and if the corresponding included angles are also equal, then the triangles are similar.
SAS Similarity Theorem Example:
Are the two triangles similar?
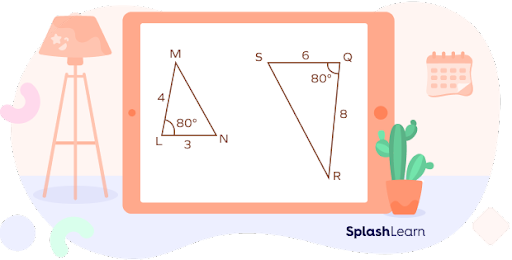
Here,
$\frac{ML}{RQ} = \frac{LN}{QS} = \frac{1}{2}$
m∠ L = m∠ Q $= 80^{\circ}$
By SAS similarity rule, ΔMLN ≅ ΔQRS
Facts about SAS theorem
- SAS theorem is applicable to all types of triangles as long as the conditions of the SAS rule are satisfied.
- The positions of letters in SAS are significant. It refers to the combination of sides and angles used to prove the congruence or similarity. Since the angle A lies between two sides (S), we use the term “included angle.”
Conclusion
In this article, we learned about the SAS theorem for both congruence and similarity rule examples. Now let us practice solving problems on the SAS Theorem.
Solved Examples on SAS Theorem
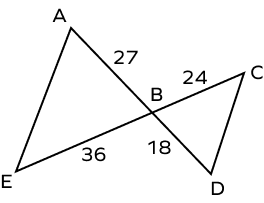
1. Are triangles ABC and BCD similar?
Solution:
In ΔABC and ΔBCD,
$\frac{AB}{BD} = \frac{27}{18} = \frac{3}{2}$
$\frac{EB}{BC} = \frac{36}{24} = \frac{3}{2}$
Thus, $\frac{AB}{BD} = \frac{EB}{BC}$
Also, ∠ABE = ∠CBD (vertical angles)
Thus, ΔABC~ ΔBCD by SAS similarity rule
2. Prove that ΔYXZ ≅ ΔSRT.
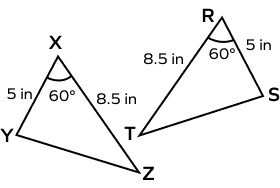
Solution:
XY = RS = 5 in
XZ = RT = 8.5 in
∠YXZ is the included angle between XY and XZ.
∠SRT is the included angle between SR and RT.
∠YXZ = ∠SRT = 60°
Thus, by SAS congruence rule, ΔYXZ ≅ ΔSRT.
3. Prove that ΔABC ≅ ΔCDA.
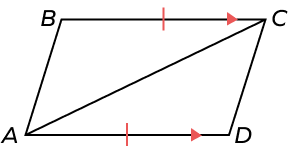
Solution:
BC = AD (given)
AC = AC (common side)
BC || AD (given)
∠DAC = ∠BCA (Alternate angles formed by a transversal cutting two parallel lines)
∠DAC is included angle between AC and AD.
∠BCA is included angle between BC and AC.
Thus, ΔABC ≅ ΔCDA By SAS congruence rule.
Practice Problems on SAS Theorem
SAS (Side Angle Side) Theorem | Definition, Congruence, Examples
What is the full form of the SAS theorem?
SAS stands for Side-Angle-Side.
In SAS theorem, the angle A refers to
In SAS theorem, A is the angle included between the given two sides.
Which of the following measurements of sides and angles are required to prove congruence using the SAS theorem?
To prove that two triangles are congruent by SAS rule, two sides and the included angle of a triangle must be congruent to two sides and included angle of another triangle.
Frequently Asked Questions on SAS Theorem
What is the difference between SAS congruence rule and ASA congruence rule?
We apply the SAS rule when two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle. The ASA congruence rule is used when two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle.
What is the difference between SAS and SSS rules?
SAS stands for “Side-Angle-Side” and SSS stands for “Side-Side-Side.” Both rules are the triangle congruence rules.
Can the SAS theorem be used to prove similarity of triangles?
Yes, SAS is the criterion in both triangle congruence and triangle similarity theorems.
















