What Is the Slope of Parallel Lines?
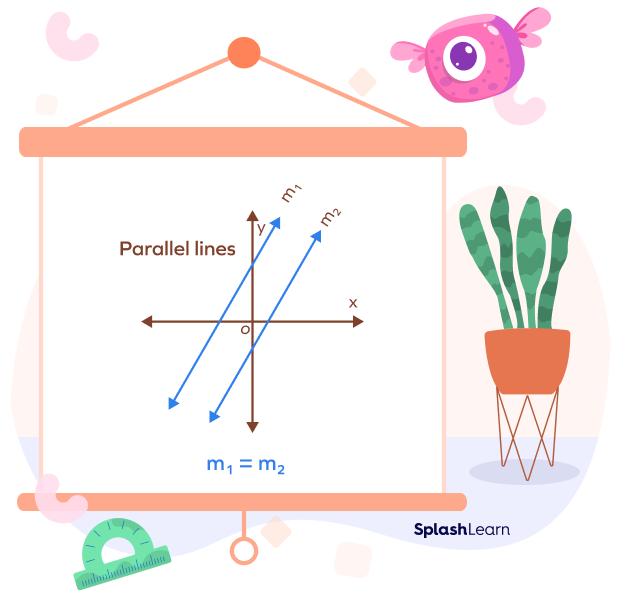
The slope of parallel lines is always equal. Parallel lines have the same slope because their rise over run ratio is equal. They make an equal angle with the positive x-axis.
In geometry, parallel lines can be defined as two lines in the same plane that never meet and are at equal distance. The slope of a line is defined as the rise over run ratio or the ratio of the change in vertical distance over the change in the horizontal distance.
If we have two parallel lines with slopes $m_1$ and $m_2$, then $m_1 = m_2$.
Conversely, if the slopes of two lines are equal, then the lines are parallel to each other.
Recommended Games
Why Is the Slope of Parallel Lines Equal?
In geometry, two or more coplanar lines that never intersect and are equidistant are parallel lines. As parallel lines always rise and run at the same rate, they never intersect and have the same slope.
Two parallel lines have the same slope but different y-intercepts. If they have the same y-intercept, they will coincide.
Slope of parallel lines examples:
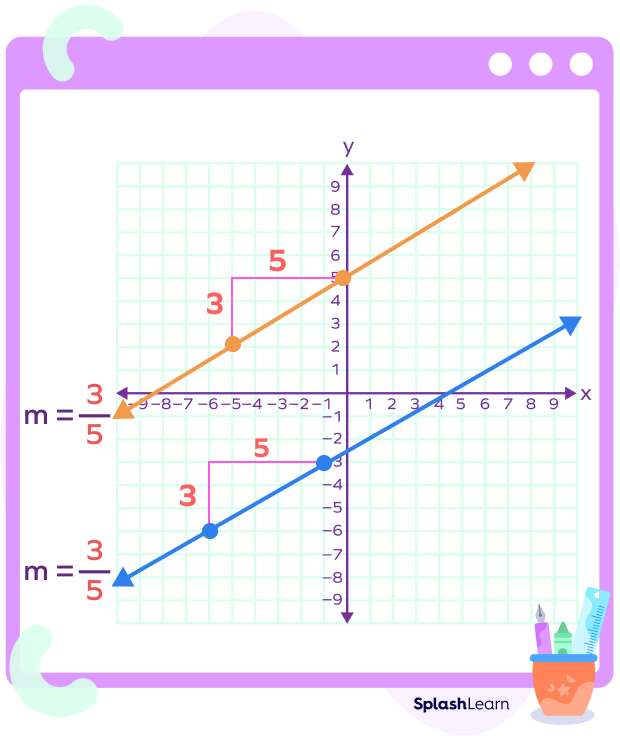
Example 1: Consider two lines having the slope of $\frac{3}{5}$. Their graph shows that they have the same rise over run ratio. These lines are parallel.
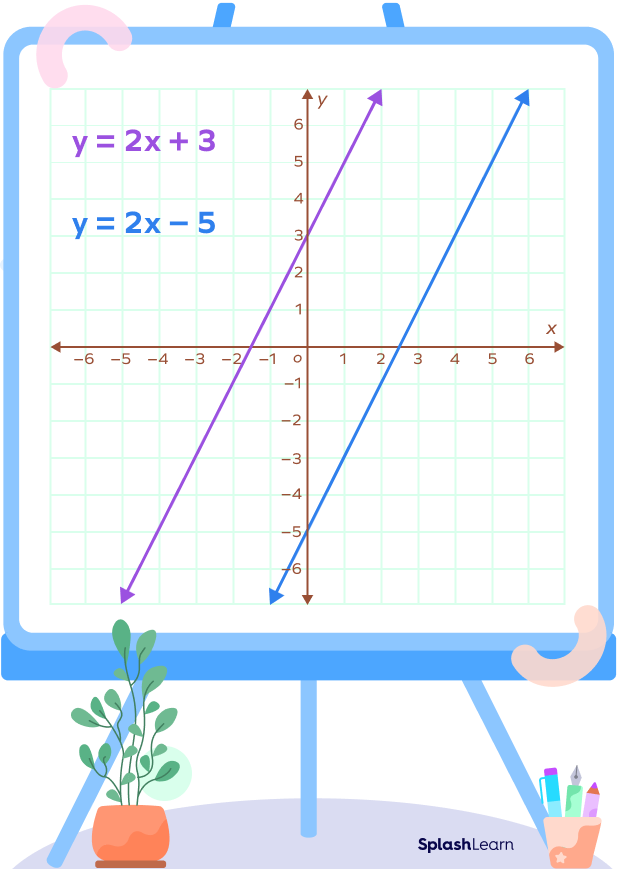
Example 2: Consider the lines $y = 2x + 3$ and $y = 2x \;-\; 5$. These two lines have the same slope, 2. However they have different y-intercepts.
How to Identify Parallel Lines
Let’s understand how to find the slope of parallel lines or how to determine whether the given equations of lines represent parallel lines or not.
Using Slope-Intercept Form
The slope-intercept form of the equation of a line is given by $y = mx + b$. Write the equations of given lines in the slope-intercept form, compare the equations with $y = mx + b$ to find the value of m (slope). If their slopes are equal, the two equations represent parallel lines.
Using General Equation
The equations representing parallel lines have equal coefficients for x and y. The line parallel to $ax + by + c_1 = 0$ has the equation of the form $ax + by + c_2 = 0$.
Derivation of Slope of Parallel Lines
If the two lines have slopes of $m_1$ and $m_2$, then the angle between them is given by
$tan\theta = \frac{m_1\;-\; m_2}{1 + m_1\;m_2}$
The angle formed between two parallel lines is either $0^\circ$ or $180^\circ$.
$tan(0^\circ)$ or $tan(180^\circ)= \frac{m_1\;-\; m_2}{1 + m_1\;m_2}$
$\Rightarrow 0 = \frac{m_1\;-\;m_2}{1 + m_1\;m_2}$ $\left[ \therefore tan(0^\circ) = tan(180^\circ) = 0\right]$
$\Rightarrow 0 = m_1\;-\;m_2$
$\Rightarrow m_1\;-\;m_2 = 0$
$\Rightarrow m_1 = m_2$
Thus, the slopes of two parallel lines are equal.
Hence, the slope of parallel lines formula is given by $m_1 = m_2$
Equation of Parallel Lines
The line parallel to $ax + by + c_1 = 0$ is $ax + by + c_2 = 0$. Here, we observe that both equations have equal coefficients for x and y. If the equation of a line is given by $y = mx + c$ then the slope of this line is equal to “m.”
Now let’s understand how to find an equation of a parallel line passing through a point with an example.
Example: Find the equation of a line passing through the point (2,3) and parallel to the line $2x − 3y + 8 = 0$.
The required line is parallel to the line $2x \;−\; 3y + 8 = 0$.
We can rewrite it as
$−3y = −2x \;−\; 8$
$y = \frac{2}{3}x + \frac{8}{3}$
The slope of the line $2x − 3y + 8 = 0$ is $m = \frac{2}{3}$.
Thus, the slope of the required line is also $\frac{2}{3}$.
The slope-point form of the equation of line is given by $y \;−\; y_1 = m (x \;−\; x1)$.
Here, $(x_1,\; y_1) = (2,\; 3)$ and $m = \frac{2}{3}$
$y \;−\; 3 = \frac{2}{3} (x \;−\; 2)$
$3y \;−\; 9 = 2x \;−\; 4$
$2x \;−\; 3y = \;−\; 5$
Facts about Slope of Parallel Lines
- Parallel lines are not always equal in length, but they are always at an equal distance from each other.
- Parallel lines do not meet.
- A triangle has no parallel line, but opposite sides of the square/rectangle are parallel, and hence, its slope is the same.
- We can draw an infinite number of lines parallel to a given line.
- All horizontal lines are parallel since the slope of horizontal lines is 0.
- Slope of vertical lines is not defined. However, all vertical lines are parallel.
Conclusion
In this article, we learned about the slope of parallel lines, how to find the slope of parallel lines, its derivation, and how to find equations of parallel lines. Let’s solve a few examples and practice problems.
Solved Examples on Slope of Parallel Lines
- Find the slope of a line parallel to $y = 5x + 4$.
Solution:
The equation of the line is $y = 5x + 4$.
On comparing it with $y = mx + c$, we get $m = 5$.
Two parallel lines have the same slope.
Hence, the slope of the line parallel to $y = 5x + 4$ must be $m = 5$.
- If the slopes of two parallel lines “p” and “q” are $4k \;−\; 1$ and $k + 8$ respectively, then find the value of “k.”
Solution:
If we have two parallel lines with slopes as $m_1$ and $m_2$, then $m_1 = m_2$.
$\Rightarrow 4k\;-\;1 = k + 8$
$\Rightarrow 4k\;-\;k = 8 + 1$
$\Rightarrow 3k = 9$
$\Rightarrow k = 3$
Hence, the value of k is 3.
- Find the slope “m” of the line $y = mx + 5$ if it passes through $(\;−\;2,\; 1)$.
Solution:
The line $y = mx + 5$ passes through $(\;−\;2,\; 1)$.
So, the point $(\;−\;2,\; 1)$ must satisfy the equation.
$\therefore 1 = m (\;−\;2) + 5$
$\Rightarrow 1\;-\;5 =−2m$
$\Rightarrow -\;4 =\;−\;2m$
$\Rightarrow 4 = 2m$
$\Rightarrow 2m = 4$
$\Rightarrow m = 2$
The required value of “m” is 2.
- Find the slope of a line parallel to $3x + 13y + 5 = 0$.
Solution:
Given the equation of the line is $3x + 13y + 5 = 0$.
To find the slope of the line, let’s express the given equation in $y = mx + c$ form.
$3x + 13y + 5 = 0$
$\Rightarrow 13y = \;-\;3x + 5$
$\Rightarrow y = \;-\;\frac{3}{13}x + \frac{5}{13}$
Here, $m = \;-\;\frac{3}{13}$
As we know, the slope of parallel lines is equal.
Hence, the slope of a line parallel to $3x + 13y + 5 = 0$ is $m =\;-\;\frac{3}{13}$.
- If a line passes through the points $(\;−\;2,\; \;−\;1)$ and $(1,\; 3)$ and another line has the slope 43. Are both lines parallel?
Solution:
Given, the first line passes through the points $(\;−\;2,\; \;−\;1)$ and $(1,\;3)$, and another line has the slope $\frac{4}{3}$.
Here, we will find the slope of the first line using the slope from the two-point formula, which is given by $m_1 = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} = \frac{3\;-\;(\;-\;1)}{1\;-\;(\;-\;2)} = \frac{4}{3}$.
Slope of the second line is given as $m_2 = \frac{4}{3}$
Since, $m_1 = m_2$
Hence, both lines are parallel.
Practice Problems on Slope of Parallel Lines
Slope of Parallel Line: Formula, Derivation, Example
The slopes of two parallel lines are
The slopes of two parallel lines are equal.
Two lines with slopes m1 and m2 are parallel if _____.
Two lines with slopes m1 and m2 are parallel if $m_1 = m_2$.
What is the slope of a line that is parallel to a line that has a slope of $\frac{1}{\sqrt{3}}$?
Parallel lines have the same slope.
Hence, the slope of a line that is parallel to a line that has a slope of $\frac{1}{\sqrt{3}}$ is also equal to $\frac{1}{\sqrt{3}}$.
The slope of a line parallel to $y = \;–\;x + 4$ is equal to
On comparing $y = \;–\;x + 4$ with $y = mx + c$, we get m $= \;–\;1$
The slope of a line parallel to $y = \;–\;x + 4$ is also equal to $–\;1$.
The lines $y = 8x + 1$ and $y = \;–\;8x + 5$ are
The line $y = 8x + 1$ has the slope 8.
The line $y = \;–\;8x + 5$ has the slope $\;–\;8$.
Two lines with slopes $m_1$ and $m_2$ are parallel if $m_1 = m_2$.
Thus, the given lines are not parallel.
Frequently Asked Questions on Slope of Parallel Lines
How can you prove that two lines are parallel?
Two lines are parallel if both lines have equal slopes.
What is the condition for three lines to be parallel to each other?
Let three lines have slopes $m_1,\; m_2$, and $m_3$. Then the condition for three lines to be parallel to each other is $m_1 = m_2 = m_3$.
What is the slope of perpendicular lines?
Two lines with slopes $m_1$ and $m_2$ are perpendicular if $m_1= \;-\;\frac{1}{m_2}$ .
What is the formula for the slope of parallel lines?
If we have two parallel lines with slopes as $m_1$ and $m_2$, then the formula for the slope of parallel lines is $m_1 = m_2$.
What is the angle between two parallel lines?
The angle between two parallel lines is either $0^\circ$ or $180^\circ$.


























