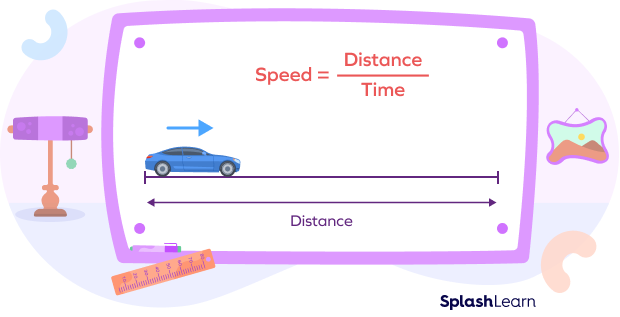
What Is the Formula for Speed in Math?
The formula for speed in math is determined by dividing the distance traveled by the time taken to cover that distance.
Speed $= \frac{Distance}{Time}$
Speed is a measure of how quickly an object moves or the rate at which an object covers a certain distance. It is a scalar quantity and is typically expressed in units such as meters per second (m/s), kilometers per hour (km/h), or miles per hour (mph).
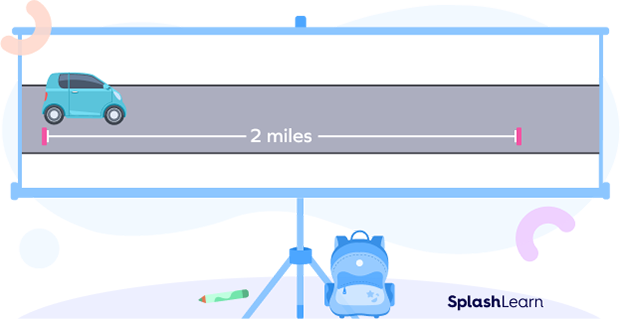
Example: Suppose that a car travels from point A to point B in half an hour. If the distance between A and B is 2 miles, what was the speed of the car?
Distance = 2 miles
Time taken = 0.5 hour
Speed $= \frac{Distance}{Time} = \frac{2}{0.5} = 4$ miles per hour
Recommended Games
Formula for Speed
A mathematical equation called the speed formula is used to determine how fast an object is moving. It is determined by dividing the total distance traveled by the time needed to complete that distance.
The formula to find speed is
Speed$ = \frac{Distance}{Time}$
S $= \frac{D}{T}$
where
S: Speed
D: Distance
T: Time
The unit of the speed calculated by this formula is dependent on the units of time and distance.
How to Calculate Speed in Math
In order to determine the speed in mathematics, it is necessary to know both the distance traveled and the amount of time taken to cover that distance. Follow this step-by-step method to calculate speed.
Step 1: Determine the total distance traveled
Note that if the problem mentions a round journey, it means that the same distance is covered twice.
Step 2: Measure or determine the time taken to cover the distance
Step 3: Use the formula for speed
Speed $= \frac{Distance}{Time}$
To find the speed, divide the distance by the amount of time taken.
Step 4: Write the answer using the correct unit of measurement.
The speed will be given in meters per second (m/s), for instance, if the distance is in meters and the time is in seconds. The speed will be expressed in miles per hour (mph) if the distance is measured in miles and the time in hours.
Speed, Distance, and Time: Formulas
| Speed | Distance | Time |
|---|---|---|
| Distance divided by time equals speed. | Speed multiplied by time equals distance. | Distance divided by speed equals time. |
| Speed $= \frac{Distance}{ Time}$ | Distance $= Speed \times Time$ | Time$= \frac{Distance}{Speed}$ |
To calculate one quantity, one must have information about the other two quantities involved.
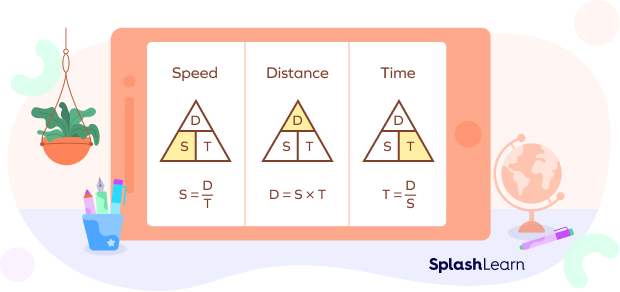
The picture given above shows three different triangles showing rearrangements of the formula of speed. The first triangle shows the formula for speed. The second and third triangles depict the formulae for distance and time, respectively.
Facts on Speed Formula
- Speed is a scalar quantity. Speed does not consider the direction of motion, only the magnitude.
- Distance is the measure of how much ground an object has covered or the total movement of an object on ground.
- Time is the measure of the duration or the interval between two events.
- Speed is inversely proportional to time. As the speed increases, the time required to travel a certain distance decreases.
Conclusion
In this article, we learned about the concept of speed and its formula, which calculates the rate of motion. Speed is a scalar quantity that considers only magnitude. To reinforce our understanding, let’s now apply the speed formula through solving examples and attempting MCQs for better comprehension.
Solved Examples on Speed Formula
1. What is the average speed of a car that travels a distance of 120 miles in 2 hours?
Solution:
Distance = 120 miles
Time = 2 hours
Use the speed formula to calculate the speed.
Speed $= \frac{Distance}{Time}$
Speed $= \frac{120 \;miles}{2 \;hours} = 60$mph
Therefore, the average speed of a car that travels a distance of 120 miles in 2 hours is 60 mph.
2. What is the average speed of a cyclist who covers a distance of 30 miles in 1.5 hours?
Solution:
Distance = 30 miles
Time = 1.5 hours
Use the speed formula to calculate the speed.
Speed $= \frac{Distance}{Time}$
Speed $= \frac{30 \;miles}{1.5 \;hours} = 20$mph
Therefore, the average speed of a cyclist who covers a distance of 30 miles in 1.5 hours is 20 mph.
3. How much distance does a train cover when traveling at a constant speed of 80 miles for 3 hours?
Solution:
Speed = 80 mph
Time = 3 hours
Use the rearranged speed formula to calculate the distance.
Distance $= Speed \times Time$
Distance $= 80\; mph \times 3\; hours = 240$ miles
Therefore, the train, when traveling at a constant speed of 80 miles for 3 hours, is 240 miles.
4. What is the time required by a car that travels a distance of 400 miles at a speed of 60 mph?
Solution:
Distance $= 400$ miles
Speed $= 60$ mph
Use the rearranged speed formula to calculate the time.
Time $= \frac{Distance}{Speed}$
Time = \frac{400 \;miles}{60 \;mph} ≈ 6.67$ hours
Therefore, for the car to cover a distance of 400 miles, it takes approximately 6.67 hours (or 6 hours and 40 minutes).
5. What will be the time a car takes at a speed of 60 miles per hour to move a distance of 180 miles?
Solution:
Distance = 180 miles
Speed = 60 miles per hour
Using the formula of time, we can calculate the time-
Time$= \frac{Distance}{Speed}$
Time $= \frac{180 \;miles}{60 \;miles\; per\; hour} = 3$ hours
Therefore, the car takes approximately 3 hours to move a distance of 180 miles at a speed of 60 miles per hour.
Practice Problems on Speed Formula
Speed Formula - Definition, Examples, Practice Problems, FAQs
What is the formula to calculate speed?
The speed formula is an accurate representation of how to calculate speed by dividing a distance by time.
What is the speed of a car that travels a distance of 120 miles in 2 hours?
Using the speed formula, we can calculate the speed-
Speed $= \frac{Distance}{Time}$
Speed $= \frac{120m}{2 \;hours} = 60$ mph
How much time does it take for a cyclist to travel a distance of 45 miles at a speed of 15 mph?
Using the derived time formula from the speed formula, we can calculate time-
Time $= \frac{Distance}{Speed}$
Time $= \frac{45m}{15m/h} = 3$ hours
What is a runner’s average speed for completing a marathon at a distance of 42.195 miles in 3.5 hours?
Using the speed formula, we can calculate the average speed:
Time$= \frac{Distance}{Speed}$
Time $= \frac{42.195 \;m}{3.5\; hours} = 12.055 \;mph$ (rounded to three decimal places)
How far did a train travel at a speed of 80 mph for 2.5 hours?
Using the derived distance formula, we can calculate the distance
Distance $= Speed \times Time$
Distance $= 80 \;m \times 2.5\; hours = 200\; m$
Frequently Asked Questions about the Speed Formula
What is the difference between speed and average speed?
Speed is a one-time calculation. Speed represents the rate of travel at a specific moment, but the average speed takes into account the different speeds maintained throughout the trip and provides an overall average rate of travel.
How do you calculate speed by using the speed formula?
Typically, the formula for speed is written as:
Speed $= \frac{Distance}{Time}$
In this equation, “Speed” denotes the rate at which an object goes, “Distance” denotes the total distance covered by the object, and “Time” denotes how long it takes for the thing to travel that distance.
How is speed different from velocity?
Speed and velocity have distinct meanings in physics. Speed is a scalar quantity that refers to the magnitude of the rate at which an object covers a distance, while velocity is a vector quantity that includes both the magnitude and direction of the object’s motion.
What is the difference between speed from acceleration?
An object’s speed is how quickly it travels, whereas its acceleration is how quickly its speed varies. Positive (speeding up) or negative (slowing down) acceleration are both possible.
What is the mileage of a vehicle?
The mileage of a vehicle refers to the distance it can travel on a certain amount of fuel. It is a measure of the vehicle’s fuel efficiency.

















