What is Count Back?
The count back strategy is one of the easiest ways to learn subtraction. Counting back will help you find out what’s left after taking one number away from another. Subtraction has many everyday applications like calculating the amount you are left with after shopping, finding the number of candies left in a bag if you eat some, etc. There are many instances where we find this method convenient to find the difference between two numbers.
Counting back is a method of learning subtraction by taking away the smaller number from the larger number by counting backward from the larger number. Here, we remove one number in every step.
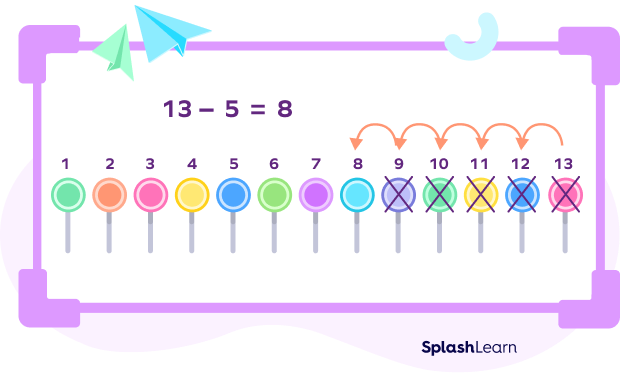
For example: Suppose that there are 13 lollipops and you eat 5 of them; how many lollipops will remain? Let’s count back to subtract 5 from 13.
On counting back, we get
$13$ $-$ $5 = 8$
The image shows how we can subtract by counting back!
Recommended Games
How Do You Count Back?
We start with the larger number and then count back the number of steps equal to the smaller number to find the difference between the two numbers.
Consider an example: If you had 8 balloons and 2 of them burst, how many balloons are you left with? We count back from 8 two times to get 6. The image shows the perfect illustration of the steps involved!

Recommended Worksheets
Minuend and Subtrahend
Let’s understand two terms related to the subtraction operation using an example.
If you take away 7 candies from 16 candies, you will be left with 9 candies.
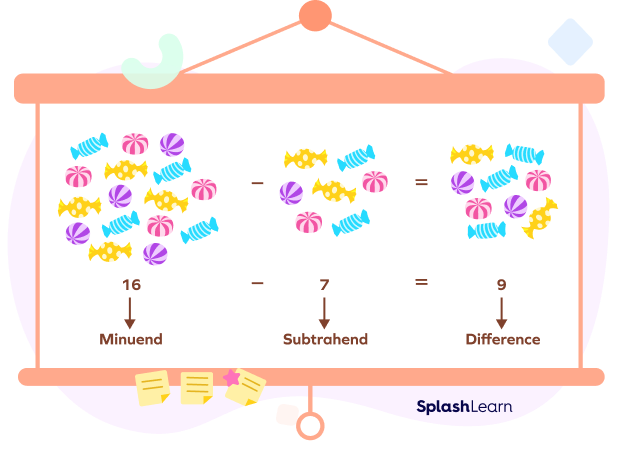
The number from which another number is being subtracted is called the minuend (Here, 16). Subtrahend is the number being subtracted from another (Here, 7).
Easy Techniques of Counting Back
Number Line Technique
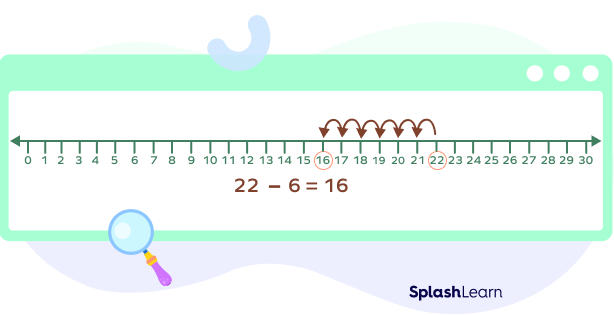
In this technique, you first mark the larger number (minuend) on the number line from which you want to subtract the smaller number (subtrahend). Now, count back the number of steps equal to the subtrahend. The new point obtained is the difference between the two numbers.
For example: If you want to find the answer for 22 – 6, mark 22 on the number line, and then count back 6 steps to reach the answer, which is 16.
Finger Counting Technique
In this technique, you have to draw out the fingers to the extent of the smaller number to count back from the larger number.
For example, if you want to calculate 8 – 2, draw out 2 fingers and then count from 8 backwards using the two fingers. The number that will come on the last finger while counting back will be your answer. So, you will count backward from 8 on your two fingers as 7 and 6. The number 6 is the answer.

Tips and Tricks to Count Back
Let’s check out some fun tips and tricks that we can use!
Reach a Friendly Number
By a friendly number, we mean a number that is easy to deal with or work with. For example, multiples of 10 are friendly since they are easy to add and subtract. When you are dealing with relatively difficult numbers, first try to reach the nearest multiple of 10 (or the friendly number) by subtracting a convenient part of the smaller number from the larger number. Finally, subtract the balance of the smaller number from the friendly number.
For example, let’s subtract 26 from 96 using this trick. First, subtract 6 from 96 to reach the friendly number 90. Next, subtract the balance 20 from 90 to get the answer, which will be 70.
Subtrahend Breaking Trick
In this trick, you can break the subtrahend (smaller number) into ones and tens (using the place values), as they are easier to subtract (by counting back), and then subtract them from the larger number.
For example: If you want to calculate $853$ $-$ $283$, first break 283 as $200 + 80 + 3$.
Subtract 200 from 853 to get 653. Subtract 80 from 653 to get 573 and then finally subtract the remaining 3 from 573 to get the answer, which will be 570.
In equation, the example can be written as
$283 = 200 + 80 + 3$
Now, $853$ $-$ $200 = 653$
$653$ $-$ $80 = 573$
$573$ $-$ $3 = 570$, i.e., the final answer.
Count Back Facts in Math
- Here are other terms we sometimes use to say ‘count back’: Counting backwards, Counting down, Backward counting
- Counting back in twos: Subtracting 2 from the larger number at each step of counting
So, counting back in ‘n’ means we subtract the number n from the larger number at every step in counting backwards.
Solved Examples
1. Calculate 76 – 24.
Solution: Break 24 into 20 and 4. Then deduct 20 from 76 by counting back 20 steps from 76, and you will get 56. Now, count 4 numbers back from 56 to get the answer as 52.
2. What is the answer to the question 50 – 35?
Solution: Break 35 into 30 and 5. Count 30 steps back from 50, i.e., 20, and then 5 steps from 20, i.e., 15, which is the required answer.
3. Imagine it is your birthday and you have received 12 candies from which you give: 4 candies to one friend, 2 candies to another friend, and 3 candies to your third friend. How many candies remain with you?
Solution: First, take 12 on the number line and then count 4 steps backward.
You are left with 8 candies.
$12$ $-$ $4 = 8$
Now, count 2 steps back.
You are left with 6 candies.
$8$ $-$ $2 = 6$
And at last, count 3 steps back.
$6$ $-$ $3 = 3$
Finally, only 3 candies remain with you.
Practice Problems
Count Back
What is the answer for $27$ $-$ $4$?
Using the number line method, you will get $27$ $-$ $4 = 23$
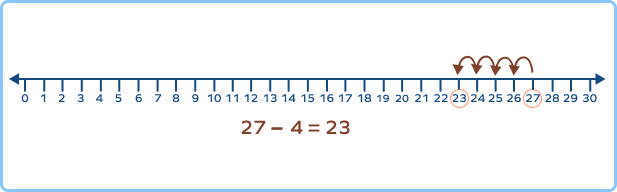
Jack has $\$$$123$. What is the amount left if he spends $\$$$93$?
We have to subtract $93$ from $123$ to find the amount left with Jack.
Using the friendly number trick, count $3$ steps back from $123$ to get $120$ $\left(\text{a friendly number}\right)$. Next, subtract the balance $90$ $\left(93-3=90\right)$ from $120$ to get the final answer.
$120-90=30$.
So, Jack now has $\$$30 left with him.
Find the difference $365 - 173$.
Let’s use the subtrahend breaking trick.
Here, $173 = 100 + 70 + 3$
$365 - 100 = 265$
$265 - 70 = 195$ (Here, you can again break $70$ as $65 + 5$ to make it easier!)
$195 - 3 = 192$
Frequently Asked Questions
With more practice, time, and effort, the process of mental counting gets easier.
What is the meaning of “count on”?
Count on is a method of adding numbers and is the opposite of counting back, and it concerns the subtraction of numbers.
How does addition help in counting back?
Consider an example: Subtract 5 from 14, i.e., $14$ $-$ $5$.
To do this, you can also think about the number that can be added to 5 to get 14.
$5 + 9 = 14$.
Since an inverse relationship exists between addition and subtraction, 9 will be the difference. Addition helps you to verify your answer.
How does the compensation strategy help in counting back?
Compensation refers to adding or subtracting numbers according to your convenience to make the equation easy to solve.
For example, let’s solve $16$ $-$ $9$.
Subtracting 10 from 16 is easy. Here, the number 1 will be subtracted extra from 16.
$16$ $-$ $10 = 6$
Finally, add 1 to 6 to compensate.
$6 + 1 = 7$.




































