Double Minus 1
Different strategies of addition help us build a strong sense of numbers and solve problems easily. It inculcates in us an ability to add numbers mentally. In this lesson, we will work to understand one such addition strategy: doubles minus one. This strategy is close to doubles facts and is known as the near doubles strategy.
Recommended Games
What Are Doubles Facts?
To double a number means we get to add the same numbers twice. A doubles addition fact is a math fact where we add two same numbers. Let’s review the doubles fact from $1$$–$$10$.
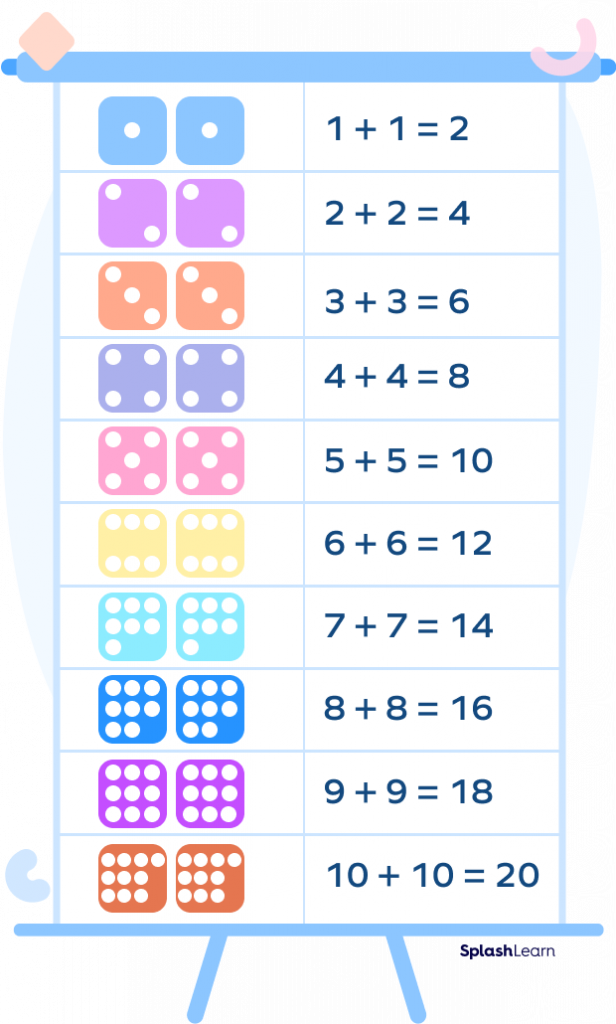
We notice that the doubles or the sum of two identical numbers are always even.
Understanding the concept of doubles facts will help us manipulate numbers and use different strategies to solve various math problems. We apply this fact to find sums for near-double facts. Let’s dive in and learn how to add numbers using the doubles minus 1 strategy.
Recommended Worksheets
What Is the Double Minus One Strategy?
Now that we recognize doubles facts, we can apply them to add two consecutive numbers.
Let’s explore more by helping Chi. Chi has a tray of eggs that has 6 eggs in one row, and the other row has 5 eggs. Help Chi to find how many eggs he has in all.
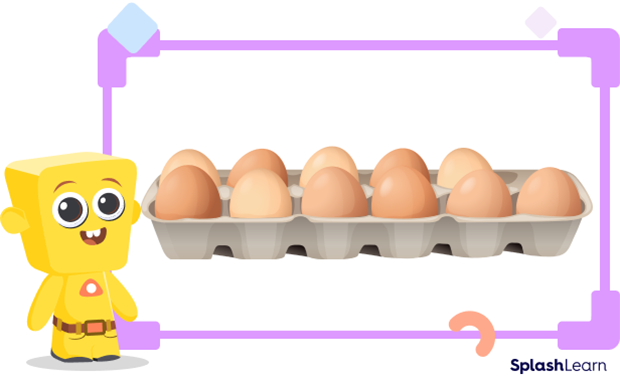
Chi wants to solve $6 + 5$. We can find the total by counting all the eggs. However, we can use our knowledge of doubles facts to get the answer quickly.
He knows that when the two rows of trays have six eggs each, there are 12 eggs. In other words, $6 + 6 = 12$. We can use this ‘doubles fact’ to find the solution.
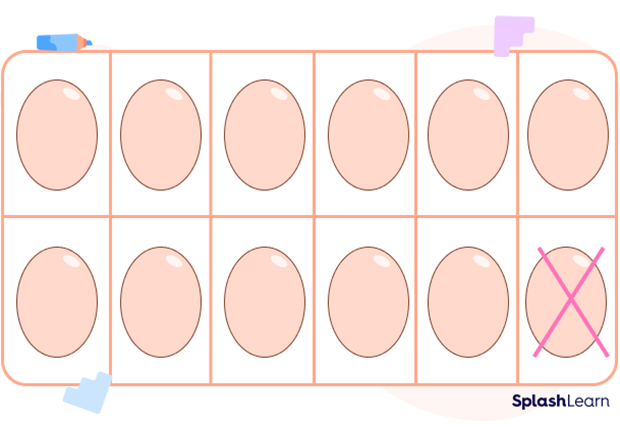
We know that 5 is one less than 6. Since $6 + 6 = 12, 6 + 5$ is one less than $6 + 6$ or 12. So, $6 + 5$ is one less than 12 or 11. Therefore, Chi has 11 eggs.
We can add two consecutive numbers using the double minus one strategy. It is done by adding the larger number twice or doubling it and subtracting one from it to get the final answer.
For example, use $8 + 8 = 16$ to find the sum of 8 and 7.
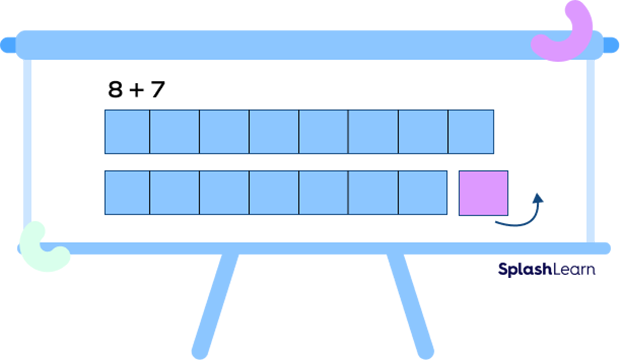
Since 7 is one less than $8, 8 + 7 = 8 + 8$ $-$ $1 = 16$ $–$ $1 = 15$
Difference between Doubles and Double Minus One Strategy
When we speak about doubles, we refer to adding a number to itself. The resulting answer that we obtain is called double of the number. In contrast, the doubles minus one strategy is a way to obtain the sum of two consecutive numbers. In this process, we simply double the bigger of the two numbers and subtract one from it to get the sum of two numbers.
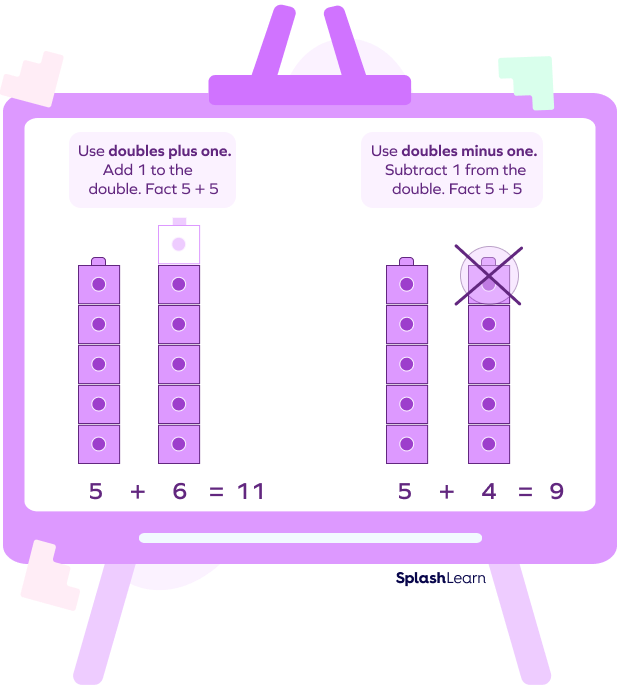
Difference between Doubles Plus One and Doubles Minus One
We can also use the near doubles strategy on two numbers to add them. The double plus one and double minus one strategies derive the sum of two consecutive numbers. Let’s understand their difference with the following example.
Solved Examples
1. Use the following fact to find 4 + 3.
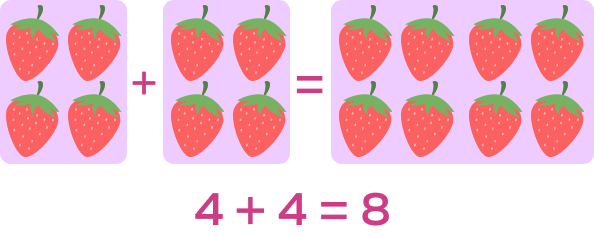
Solution:
$4 + 3$ is one less than $4 + 4$ or double of 4.
Since $4 + 4 = 8, 4 + 3 = 8$ $-$ $1 = 7$.
2. Complete the following sentence.
$12 + 11 = 12 + 12$ $– \underline{}$
Solution:
Since 11 is one less than 12. $12 + 11$ is one less than the double of 12.
So, $12 + 11 = 12 + 12$ $-$ $1$.
Therefore, the missing number is 1.
3. Write the double fact that will help you solve the following problem.
7 ducks were swimming in a pond. 6 more ducks joined them. How many ducks are in the pond now?
Solution:
To find the total number of ducks, we need to solve $7 + 6$. Since $7 + 6$ is one less than $7 + 7$, we can use the double fact $7 + 7 = 14$ to solve this problem.
Since $7 + 7 = 14, 7 + 6 = 14$ $-$ $1 = 13$
Practice Problems
Doubles Minus 1 - Definition with Examples
Which of the following can be solved using the following double fact?
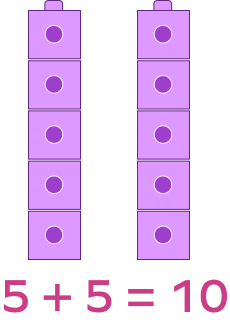
Since $5 + 6$ is one more and $5 + 4$ is one less than the given fact. We can use the fact to solve $5 + 6$ and $5 + 4$.
If $7 + 7 = 14$, which of the following equals $7 + 6$?
Since $7 + 7 = 14, 7 + 6 = 7 + 7$ $–$ $1 = 14$ $–$ $1 = 13$
Which doubles fact helps you solve $9 + 8$ using the double minus one strategy?
$9 + 8$ is one less than the double of $9$ or $9 + 9$.
Frequently Asked Questions
Is there a mathematical benefit to learning the double minus 1 strategy?
By learning double facts, you will be able to find the sum of many different addition problems in mathematics. The near-double facts will be helpful when you have many different calculations to perform.
Write the near-double facts of $7 + 7 = 14$ where we use the double plus one or double minus one strategy.
The near-double facts depend on the addend of the doubles facts. The near-double facts of $7 + 7 = 14$ are listed below.
$8 + 7 = 15$
$7 + 6 = 13$
$7 + 8 = 15$
$6 + 7 = 13$
Do we always pick the bigger of two digits to find their double in the double minus one and double plus one strategy?
We use the double plus one or minus one strategy to find the sum of two consecutive numbers. In the case of double plus one, $\text{A} + \text{A} + 1$, we use the double fact of the smaller number. And in the case of double minus one, $\text{A} + \text{A} – 1$, we use the double fact of the bigger number.




































