Subtract Fractions with Unlike Denominators – Definition with Examples

How to Subtract Fractions with Unlike Denominators

Subtracting fractions with unlike denominators is not a straightforward process as subtracting fractions having the same denominator. 

Fractions represent the parts of a whole. A fraction has two parts. The number on the top of the line is called the numerator. It tells how many equal parts of the whole or collection are taken. The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into or the total number of the same objects in a collection. 

When the whole is divided into equal parts, the number of parts we take makes up a fraction. 

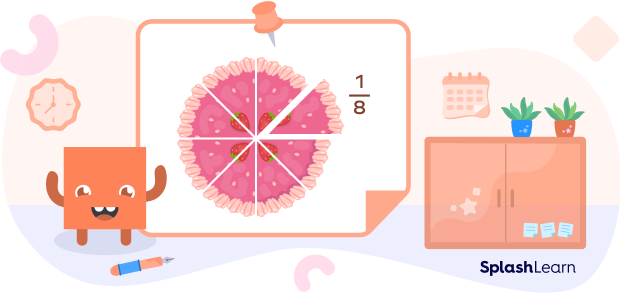
If a cake is divided into eight equal pieces and each piece of cake represents $\frac{1}{8}$ of the whole cake. It is read as “one-eighth” or “1 by 8.”

Types of Fractions

There are two types of fractions based on the value of the denominator.

• Like Fractions: Fractions with same denominators are known as like fractions or fractions with like denominators such as $\frac{1}{7}$ and $\frac{3}{7}; \frac{2}{5}$, and $\frac{4}{5}$.
• Unlike Fractions: Fractions with different denominators are known as unlike fractions or fractions with unlike denominators such as $\frac{1}{7}$ and $\frac{3}{8}; \frac{2}{9}$, and $\frac{4}{11}$.

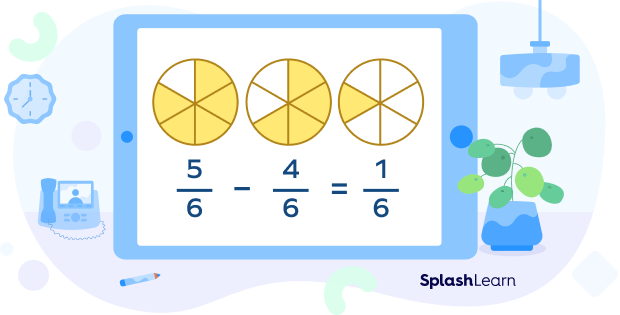
The operations on like fractions is quite easy. Suppose we have to subtract $\frac{5}{6}$ from $\frac{4}{6}$. Since, the fractions are like, only the numerators will be subtracted and the denominator will remain the same, i.e., $\frac{5}{6}\;-\;\frac{4}{6} = \frac{1}{6}$

Visually, we represent it as follows:

When it comes to the fractions with unlike denominators, it is a little bit tricky. How can we subtract fractions with different denominators? Well, let’s learn how to subtract fractions with different denominators step by step using different methods.

Methods to Subtract Fractions with Unlike Denominators

Method I

This is the LCM method. The basic rule for subtracting fractions with different denominators is to make the denominators the same by finding the LCM of the two denominators.

Step 1: Find the least common multiple, i.e., LCM of the two denominators.
Let’s find $\frac{5}{6} \;-\; \frac{2}{9}$. 

To find the LCM of 6 and 9, we write the prime factorization of 6 and 9 using exponents:
$6 = 2 \times 3$ 

 $9 = 3 \times 3 = 3^{2}$

Here, the highest power of 2 is 2. The highest power of 3 is $3^{2}$.

Find the product of the factor terms that have the highest power. 

LCM of 6 and $9 = 2 \times 3^{2} = 18$

Step 2: Convert both the fractions into like fractions by making the denominators same (i.e., by finding the equivalent fractions). In this example, we get 

 $\frac{5 \times 3} {6 \times 3} = \frac{15}{18}$ and $\frac{2 \times 2}{9 \times 2} = \frac{4}{18}$

Step 3: Subtract the numerators. The denominator stays the same.

$\frac{15}{18} \;-\ \frac{4}{18} = \frac{15 – 4}{18} = \frac{11}{18}$

Step 4: Convert the resultant fraction to its simplest form if the GCF of the numerator and denominator is not 1. 

In this case, the GCF $(11, 18) = 1$. So, it is already in its simplest form. 

Method II 

Sometimes, there are cases when one denominator is the multiple of another denominator. Consider an example. Let’s subtract $\frac{12}{39}$ from $\frac{16}{13}$. 

Multiplying big numbers can be time-consuming and lengthy. So, we will use the following steps:

Step 1: Since one denominator is multiple of the other, we can easily make the denominators the same. Multiply both the numerator and denominator of $\frac{16}{13}$ by 3. 

$\frac{16 \times 3}{13 \times 3} = \frac{48}{39}$

Step 2: Subtracting the two fractions. In this example, we get 

$\frac{48}{39} \;-\; \frac{12}{39} = \frac{36}{39}$

Step 3: Convert the fraction into the simplest form. In this example, we get

$\frac{36}{39} = \frac{12}{13}$

Method III

Let’s discuss the cross multiplication method. As the name suggests, we cross multiply as shown below.

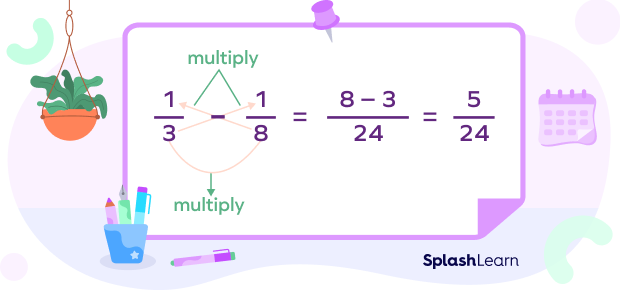
The cross multiplication method works for all cases, but it is convenient to use when the denominators are small numbers. 

Let’s subtract $\frac{5}{7}$ from $\frac{1}{2}$ by cross multiplication.

$\frac{5}{7} \;-\; \frac{1}{2} = \frac{(5 \times 2)\;-\;(7 \times 1)}{7 \times 2} = \frac{10\;-\;7}{14} = \frac{3}{14}$

Subtracting Mixed Fractions with Unlike Denominators 

Mixed numbers or mixed fractions have a whole number part and a fractional part. Some examples of mixed fractions with unlike denominators are $2\frac{1}{6}$ and $5\frac{2}{5}$. Let’s understand how to subtract mixed numbers with unlike denominators by converting them into improper fractions. Subtracting improper fractions follows the same methods that we discussed earlier.

Suppose we have to subtract $2\frac{1}{6}$ from $5\frac{2}{5}$. We use the steps given below:

Step 1: Convert the mixed numbers into improper fractions. In this case, we get

$2\frac{1}{6} = \frac{12 + 1}{6} = \frac{13}{6}$ and $5\frac{2}{5} = \frac{25 + 2}{5} = \frac{27}{5}$. 

Step 2: Find the LCM of the denominators and make the denominators same. In this case, LCM $(5, 6) = 30$

 $\frac{13 \times 5}{6 \times 5} = \frac{65}{30}$ and $\frac{27 \times 6}{5 \times 6} = \frac{162}{30}$

Step 3: Subtract both the fractions. In this case, we can write all the steps together as 

$5\frac{2}{5} \;-\; 2\frac{1}{6} = \frac{27}{5}\;-\; \frac{13}{6} = \frac{162}{30} \;-\; \frac{65}{30} = \frac{162\;-\;65}{30} = \frac{97}{30}$

Step 4: Convert into a mixed number. In this case, we get $\frac{97}{30} = 3\frac{7}{10}$.

Subtracting Fractions with Unlike Denominators: Visual Model

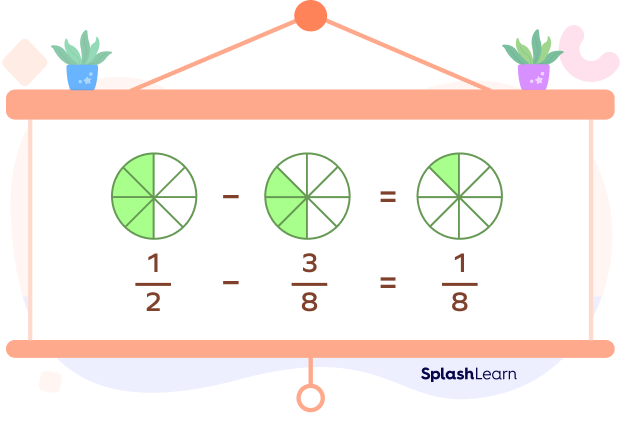
Consider one example. Suppose we have to subtract $\frac{3}{8}$ from $\frac{1}{2}$.

We can represent this subtraction visually as follows. LCM of 2 and 8 is 8. 

So, both the circles are divided into 8 equal parts. 

$\frac{1}{2} = \frac{4}{8}$

Thus, to represent $\frac{1}{2}$, we can see that 4 parts out of 8 equal parts are shaded.

To represent $\frac{3}{8}$ of a circle, 3 parts out of 8 parts are shaded. 

If we take away these three parts from the first circle, only 1 shaded part remains, which represents $\frac{1}{8}$.

Conclusion

In this article, we learned about the subtraction of fractions with unlike denominators. Let’s solve some examples for better understanding.

Solved Examples on Subtracting Fractions with Unlike Denominators

1. Subtract $\frac{3}{4}$ from $\frac{5}{6}$ using the LCM method.

Solution: 

Prime factorization of denominators 4 and 6:

$4 = 2^{2}$ and $6 = 2\times3$

LCM(4, 6) = Product of factor terms with highest powers $= 2^{2} \times 3 = 12$

$\frac{3 \times 3}{4 \times 3} = \frac{9}{12}$ and $\frac{5 \times 2}{6 \times 2} = \frac{10}{12}$

$\frac{5}{6}\;-\;\frac{3}{4} = \frac{10}{12}\;-\;\frac{9}{12} = \frac{10 \;-\; 9}{12} =\frac{1}{12}$

2. Find the difference: $\frac{1}{5}\;-\;\frac{1}{7}$.   

Solution: We will use the cross multiplication method here. 

$7 \times 1 = 7$ and $5 \times 1 = 5$. Also, $5 \times 7 = 35$

So, $\frac{1}{5}\;-\;\frac{1}{7}=\frac{7 \;-\; 5}{35} = \frac{2}{35}$

3. Jack has $\frac{4}{5}$ pounds of a papaya. If he gives $\frac{1}{3}$ pounds to Lucy, what fraction of papaya is left with Jack?

Solution: Fraction of papaya with Jack $= \frac{4}{5}$

Fraction of papaya he gave to Lucy $= \frac{1}{3}$

Fraction of papaya left with Jack $= \frac{4}{5} \;-\; \frac{1}{3}$

We will use the cross multiplication here

$\frac{4}{5}\;-\;\frac{1}{3} = \frac{12 \;-\; 5}{15} = \frac{7}{15}$

Fraction of papaya left with Jack $= \frac{7}{15}$

4. Find $\frac{3}{4}\;-\;\frac{1}{5}$.

Solution: 

We have to find the difference $\frac{3}{4}\;-\;\frac{1}{5}$.

Using the cross multiplication method, we get

$\frac{15 – 4}{20} = \frac{11}{20}$

$\frac{3}{4}\;-\;\frac{1}{5} = \frac{11}{20}$

5. Jack jumped $3\frac{1}{7}$ m in a long jump competition. Shane jumped $1\frac{2}{9}$ m. By how many meters did Jack jump longer?

Solution: Distance jumped by Jack $= 3\frac{1}{7}$ m

Distance jumped by Shane $= 1\frac{2}{9}$ m

Difference $= 3\frac{1}{7}\;-\;1\frac{2}{9}$

 $3\frac{1}{7}\;-\;1\frac{2}{9} = 2\frac{2}{7}\;-\;\frac{11}{9} = \frac{198\;-\; 77}{63} = \frac{121}{63}$

So, Jack jumped longer than Shane by $1\frac{58}{63}$ m.

Practice Problems on Subtracting Fractions with Unlike Denominators

FAQs on Subtracting Fractions with Unlike Denominators