Surface Area of Sphere

What Is the Surface Area of a Sphere?

The surface area of a sphere is the region or area covered by the outer, curved surface of the sphere. 

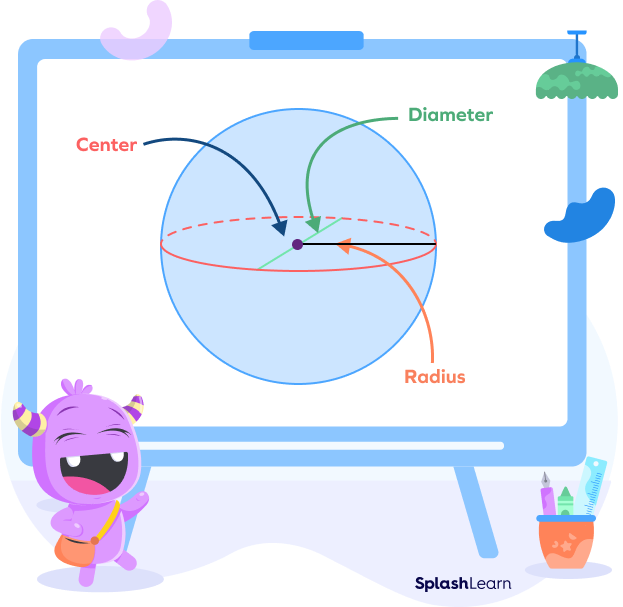
A sphere is a three-dimensional solid with every point on the surface at equal distances from the center. In simple words, any solid, round object shaped like a ball is a sphere. 

The radius of a sphere is the distance between the surface and the center of the sphere. While one endpoint of radius is on the surface, the other lies at the center of that sphere. 

Read on to know the exact definition of the surface area of a sphere, along with the derivation of the formula. 

Definition of the Surface Area of a Sphere 

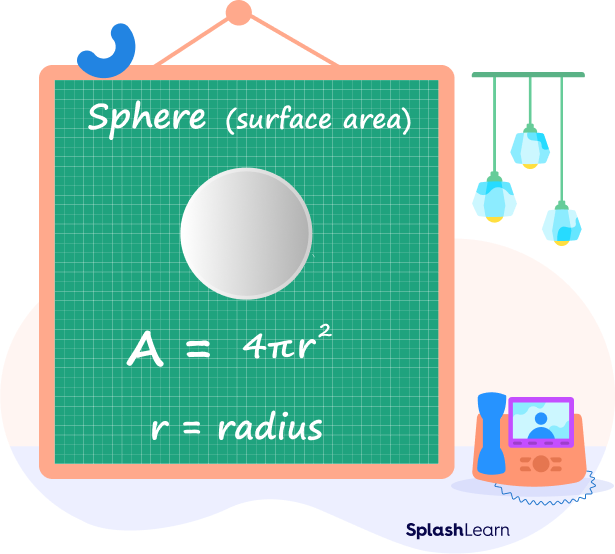
The surface area of a sphere is defined as the region covered by the sphere’s outer surface in three-dimensional space. Since the sphere is curved, its curved surface area is the same as the total area of the sphere. 

It is expressed as:

Surface area $(TSA) =$ Curved Surface Area $(CSA) = 4\pi r^{2}$ square units

Derivation of Surface Area of Sphere

Now that you have understood the surface area of a sphere, it’s time to derive the formula. 

The Greek mathematician Archimedes discovered that the surface area of a sphere is the same as the lateral surface area of a cylinder such that the radius of the sphere is the same as the radius of the cylinder and the height of the cylinder is the same as the diameter of the sphere. According to Archimedes, a sphere can fit into a cylinder so that the height of the cylinder becomes the diameter of the sphere. 

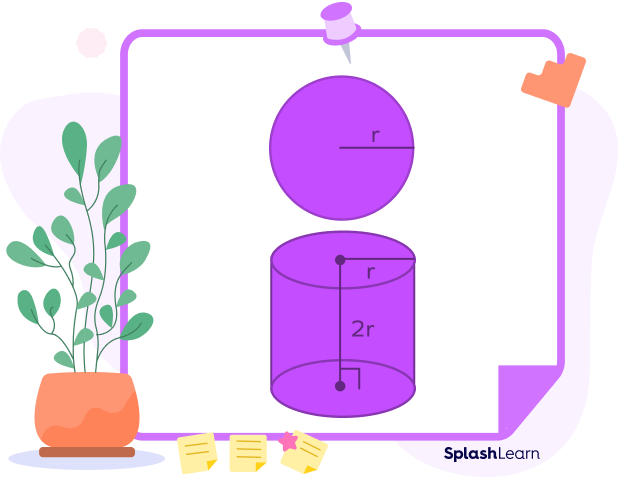
So, if the radius of a sphere and cylinder is “r,” then

Surface Area of Sphere $=$ Lateral Surface Area of Cylinder

We know that the lateral surface area of a cylinder $= 2\pi r h$, 

where “r” is the radius and ‘h’ is the height of the cylinder. 

Now the height of the cylinder = the diameter of the sphere. 

So, $h = 2r$

Substituting the value of “h” as “2r,” the surface area equation of the sphere becomes 

$2\pi r h = 2\pi r(2r) = 4\pi r^{2}$

Formula of Surface Area of Sphere

So, what’s the surface area of a sphere formula?

Surface area of the sphere $= 4\pi r^{2}$, where “r” is the sphere’s radius.

In terms of diameter, when “d” is the diameter of the sphere, the surface area of a sphere is expressed as S $= 4\pi (\frac{d}{2})^{2}$

There are three types of surface area in solids: lateral surface area (LSA), curved surface area (CSA), and total surface area (TSA). 

Curved Surface Area of Sphere

The curved surface area is the sum of areas of all the curved regions of the solid.

The curved surface area of a sphere is the same as the total surface area of the sphere since the sphere is a completely curved shape. Therefore, the formula for the curved surface area of a sphere is 

CSA of a sphere $= 4\pi r^{2}$, where “r” is the sphere’s radius.

Lateral Surface Area of Sphere

The lateral surface area of a solid figure is the area of all the regions except its top and bottom faces.

The lateral surface area of a sphere is expressed as $LSA = 4\pi r^{2}$, where r is the sphere’s radius. 

Total Surface Area of Sphere

The total surface area of a solid includes the area of all sides, including the top and bottom faces or bases.

Since the sphere has no flat surfaces, there is no difference between its curved surface area and the total surface area.

Therefore, the total surface area of a sphere $=$ the curved surface area of a sphere.

Hence, surface area $(TSA) = CSA = 4\pi r^{2}$ square units

How to Find the Surface Area of a Sphere

Let’s understand how to calculate the surface area of a sphere using an example. If the radius of a sphere is 8 cm. What will be its surface area?

The steps to find the surface area of the sphere are given below:

• Step 1: 

Note the radius of the sphere. In the above example, the radius of the sphere is 8 cm. If the diameter is given, divide the diameter by 2 to get the radius.

• Step 2:

Now, surface area of sphere $= 4\pi r^{2}$, so after substituting the value of $r = 8$, we get, surface area of sphere $= 4\pi r^{2} = 4 \times 3.14 \times 8^{2} = 4 \times 3.14 \times 64= 803.84$

• Step 3: 

Hence, the surface area of the sphere is $803.84$ $cm^{2}$

Solved Examples

1. Calculate the curved surface area of a sphere having a radius of 3 cm. Use $\pi = 3.14$. 

Solution: 

We know,

Curved surface area = Total surface area $= 4 \pi r^{2}$ square units

       $= 4 \times 3.14 \times 3 \times 3$

Therefore, the curved surface area of a sphere$= 113.04$ $cm^{2}$

2. A ball in the shape of a sphere has a surface area of $221.76$ $cm^{2}$. Calculate its diameter.

Solution: Let the radius of the sphere be r cm.

We know the surface area of a sphere $=4\pi r^{2}$

        $221.76$ $cm^{2} = 4\pi r^{2}$

                        $r^{2} = 221.76/4 \pi$

  $r = \sqrt{17.64}$

  $r = 4.2$cm

Therefore, the diameter of the sphere $= 4.2 \times 2= ​8.4$ cm.

3. A spherical ball has a surface area of 2464 sq. feet. Find the radius of the ball.

Solution: The surface area of a sphere $= 2464$ sq. feet

We know the surface area of a sphere (SA) $= 4 \pi r^{2}$

       $2464$ $cm^{2} = 4 \pi r^{2}$

                                                      $2464$ $cm^{2} = 4 \times \frac{22}{7} \times r^{2}$

                                                                    $r = 14$ feet

4. Find the ratio between the surface areas of two spheres whose radii are in the ratio of 4:3.

Solution: 

Given that the ratio between the radii of two spheres $= 4:3$

We know that,

The surface area of a sphere $= 4\pi r^{2}$

From the equation, we can say that the surface area of a sphere is directly proportional to the square of its radius.

$\Rightarrow \frac{A_{1}}{A_{2}} = \frac{r^{2}_{1}}{r^{2}_{2}}$

$\Rightarrow \frac{A_{1}}{A_{2}} = \frac{16}{9}$

Therefore, the ratio between the two spheres’ total surface areas is 16:9.

5. Find the cost required to paint a spherical ball with a radius of 10 feet. The painting cost of the ball is $\$4$ per square feet.

Solution: 

Given that the radius of the ball $= 10$ feet

We know that,

The surface area of a sphere $= 4 \pi r^{2}$ square units

$= 4 \times (3.14) \times (10)^{2}$

$= 1256$ square feet

Hence, the total cost to paint the ball $= 4 \times 1256 = \$5024$

Practice Problems

Frequently Asked Questions