Surface Area of Triangular Pyramid: Introduction
The surface area, or total surface area (TSA), of a triangular pyramid, is the total area of its 4 faces. Even though we have formulas to find the surface area of a pyramid with a triangular base, the basic idea of finding the surface is to add the areas of all the faces. It is measured in square units such as $in^{2}$, $ft^{2}$, etc.
There are many types of pyramids, and all pyramids are named by the shape of their bases. For example, a pyramid, which has a rectangular base is a rectangular pyramid; the one that has a pentagon as a base is a pentagonal pyramid, and so on. So, a triangular pyramid has a base that is triangular in shape. Let’s first learn about triangular pyramids.
Recommended Games
What is a Triangular Pyramid?
A triangular pyramid is a pyramid with a triangle as a base and 3 triangular faces. These 3 lateral triangular faces meet at one vertex. All triangular-based pyramids, either regular or irregular, have 4 vertices. They have 6 edges, out of which 3 are along the base and 3 are extending up from the base. Take a look at the image given below to understand its components.
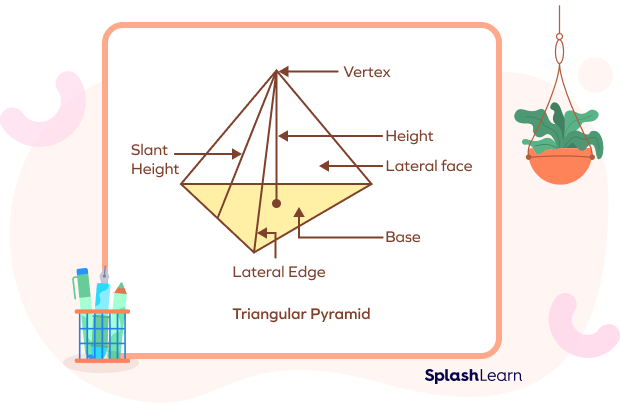
Recommended Worksheets
How to Find the Surface Area of a Triangular Pyramid
A triangular pyramid has two types of surface areas: The lateral surface area and the total surface area. You can find the surface area of a triangular pyramid by adding the lateral area of the pyramid (three triangles) to the area of the pyramid’s base (a triangle again). Let us study both in detail.
Lateral Surface Area
The lateral surface area is the area of the side faces, or we can say lateral surface area (LSA) does not include the base. It can be calculated by subtracting the base from the total surface area.
Lateral Surface Area of a Triangular Pyramid Formula

The lateral surface area of a triangular pyramid is calculated using the following formula:
The lateral surface area of a triangular pyramid $= \frac{1}{2}$ (Perimeter of the base $\times$ Slant height)
We know that the base is a triangle. So, the perimeter of the base would be, $3 \times$ side for equilateral triangles.
The lateral surface area of a triangular pyramid $= \frac{3}{2}$ (side slant $\times$ height)
$= \frac{3}{2}(b \times l)$
Where, $b =$ side of the base triangular base
$s =$ slant height
Total Surface Area
The total surface area of an object is the total area of the object’s surface. Thus, the total surface area is the sum of the base area and lateral surface area of the pyramid.
Total Surface Area of a Triangular Pyramid Formula

Here, h is the height of the pyramid. l is the slant height of the pyramid.
The total surface area of a triangular pyramid is calculated using the following formula:
The total surface area of a triangular pyramid $=$ Base Area $+$ Lateral Surface Area
As we know, Area of a triangle $= 1\frac{2} \times$ base $\times$ height
Total surface area of triangular pyramid $= (\frac{1}{2} \times$ Side of base $\times$ Height of base) $+ \frac{3}{2}$ (b $\times$ l)
$= \frac{1}{2} \times$ (b $\times$ h) $+ \frac{3}{2}$ (b $\times$ l)
where, $h =$ the height of the base triangle
$b =$ the side of the triangular base
$l =$ slant height
Fun Facts!
- A triangle-based pyramid is unique in comparison to other pyramids, as it only consists of one kind of 2D shape, a triangle.
- A triangular pyramid has 4 triangular faces, 6 edges, and 4 vertices.
- Triangular pyramids can be regular, irregular, and right-angled.
- The base of a triangle pyramid can be any type of triangle, but is usually an equilateral triangle. This means that all sides and faces are the same.
- The net of a triangle-based pyramid folds out to a large triangle made up of 4 smaller triangles.
- The base of a right triangular pyramid is a right triangle.
Conclusion
In this article, we learned in detail about the triangular pyramid definition, and formulas and facts. Let’s solve some examples and practice problems to understand it better.
Solved Examples
1. Determine the total surface area of a triangular pyramid whose base area is 36 sq. in, the perimeter of the triangle is 24 in, and the slant height of the pyramid is 28 in.
Solution:
Given data:
Area of the triangular base $= 36\; in^{2}$
The slant height (l) $= 28$ in
Perimeter (P) $= 24$ in
We know that,
Total surface area (TSA) of a triangular pyramid $= \frac{1}{2}$ perimeter of the base $\times$ slant height $+$ base area
Thus, TSA $= (\frac{1}{2} \times 24 \times 28 ) + 36$
$= 12 \times 28 + 36$
$= 336 + 36$
$= 372\; in^{2}$
Hence, the total surface area of the given pyramid is $372\; in^{2}$.
2. Find the total surface area of a triangular pyramid with base lengths of 10 and base height of 8.7 and slant height of 14. (Note: Base is an equilateral triangle.)
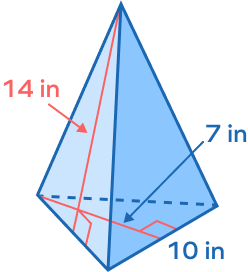
Solution:
Given data:
Base length $= 10$ in
Base height $= 7$ in
Slant height $= 14$ in
Firstly, we need to find the perimeter and the area of the base.
We know that, Area of base (triangle) $= \frac{1}{2} \times$ base $\times$ height
$= \frac{1}{2} \times 10 \times 7$
$= 35\; in^{2}$
Now, perimeter of the base of triangle $= 10 + 10 + 10$
$= 30$ in.
The total surface area (TSA) of a triangular pyramid $= (\frac{1}{2} \times$ perimeter of the base $\times$ slant height$) +$ Base area
Thus, TSA $= \frac{1}{2} \times 30 \times 14 + 35$
$= 15 \times 14 + 35$
$= 210 + 35$
$= 245\; in^{2}$
The total surface area of a triangular pyramid is $245\; in^{2}$.
3. Find the lateral surface area of a triangular pyramid with slant height 10 inch and base perimeter 24 inch.
Solution:
Given data:
Base perimeter $= 24$ in
Slant height $= 10$
The lateral surface area of a triangular pyramid $= \frac{1}{2} ($Perimeter of the base $\times$ Slant height$)$
$= \frac{1}{2} \times 24 \times 10$
$= 120\; in^{2}$
The lateral surface area of a triangular pyramid is $120\; in^{2}$.
4. Find the base length of a triangular pyramid with a slant height of 16 ft and a lateral area of 360 sq. ft.
Solution:
Lateral surface area = 360 sq. ft
Slant height = 16 ft
The lateral surface area of a triangular pyramid (LSA ) $= \frac{3}{2} (b \times l)$
$360 = \frac{3}{2} (b \times 16)$
$360 = \frac{48 \times b}{2}$
$720 = 48 \times b$
$b = \frac{720}{48}$
$b = 15$ ft.
The base length of a triangular pyramid shaped museum is 15 ft.
5. Find the slant length of a triangular pyramid with a base of 8 units and a lateral area of 120 sq. units.
Solution:
Base side $= 8$ units
Lateral Surface Area ( LSA) $= 120$ sq. units
We know that, the lateral surface area of a triangular pyramid $= \frac{3}{2} (b \times s)$
$120 = \frac{3}{2} \times 8 \times s$
$120 = \frac{24 \times s}{2}$
$240 = 24 \times s$
$s = \frac{240}{24}$
$s = 10$ sq. units
The slant length of a triangular pyramid is 10 sq. units.
Practice Problems
Surface Area of Triangular Pyramid
Identify the triangular pyramid from the shapes given below.
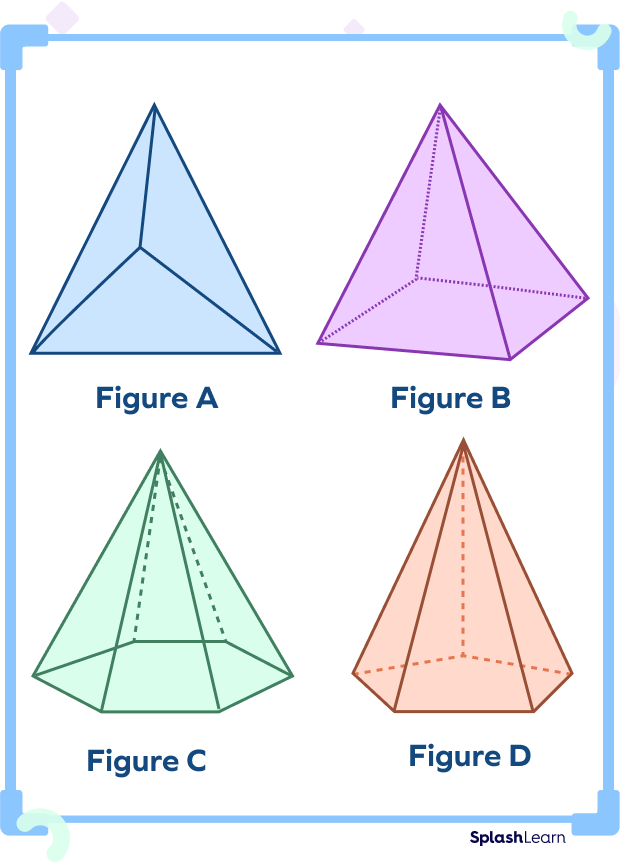
Figure A represents a triangular pyramid with a triangle as a base and 3 lateral triangular bases. Fig B, C, and D represent a square pyramid, hexagonal pyramid, and pentagonal pyramid respectively.
The base of a right triangular pyramid is a __________.
All the pyramids are named by the shape of their bases. Thus, the base of a right triangular pyramid is a right triangle.
A triangular pyramid _________ vertices.
A triangular pyramid has 4 vertices.
The formula to calculate the total surface area of a triangular pyramid is ________.
Total surface area is the sum of the base area and lateral surface area of the pyramid.
Thus, the total surface area of a triangular pyramid $= (\frac{1}{2} \times base \times height) + \frac{3}{2} (b \times s)$
$= \frac{1}{2}( a \times b ) + \frac{3}{2} ( b \times s )$
Which of the following is an incorrect statement about a triangular pyramid?
Surface area of triangular pyramid is measured in cubic units such as in$^{3}$, ft$^{3}$, etc.
Surface area of triangular pyramid is measured in square units such as in$^{2}$, ft$^{2}$, miles$^{2}$, etc.
Frequently Asked Questions
Is a triangular pyramid called a tetrahedron?
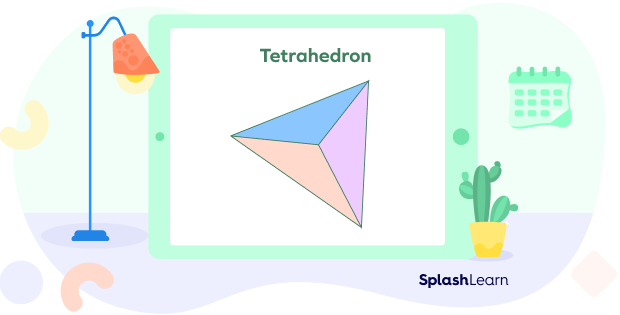
A tetrahedron is a triangular pyramid in which all the faces are triangles of equal size. All the triangles of the tetrahedron are congruent and when all the sides of all the triangles are equal, then it is a triangular pyramid with an equilateral triangle and is called a tetrahedron.
How do you find the volume of a triangular pyramid?
The volume of a 3D figure refers to its capacity, or the space occupied by it. It is measured in cubic units. Knowing the base area and height of a triangular pyramid is enough to calculate its volume. The volume of a triangular pyramid is given by the formula $\frac{1}{3} \times$ base area $\times$ height
Now consider a regular triangular pyramid made of equilateral triangles of side “$a$.”Regular Triangular Pyramid Volume $= \frac{a^{3}}{6\sqrt{2}}$ cubic units.
What are some real-life examples of a triangular pyramid?
A common example of a triangular pyramid is the pyramix or the Rubik’s triangle. It has a triangular base and 3 other triangular faces.

What are the types of triangular pyramids?
There are three types of triangular pyramids.They are as follows:
- Regular triangular pyramids.
- Irregular triangular pyramids.
- Right-angled triangular pyramids.
What does a net of a triangular pyramid look like?
The image below shows what a net of a triangular pyramid looks like.
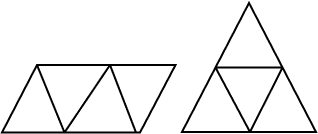
The net of a 3D shape is what it looks like if it is opened out flat. The net of a triangular pyramid has 3 triangular faces and 1 triangular base.




































