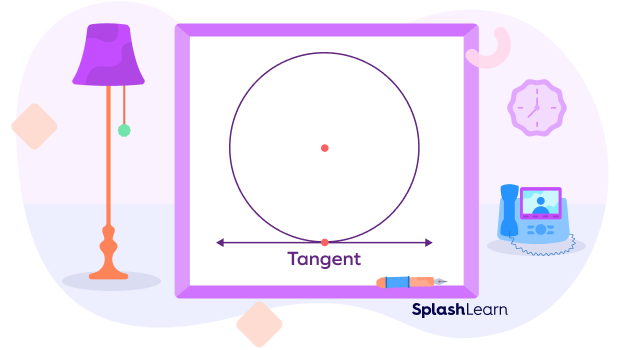
What Is The Tangent of a Circle?
The word “tangent” originated from the Latin word “tangere,” which means “to touch.” The tangent of a circle refers to a line that touches a circle at a single point.
In the image shown below, the line l is a tangent to the circle with the center C.

A straight line that touches or intersects the circle at only one point is called a tangent of the circle. A tangent touches the circle externally.
Tangent of a Circle: Definition
Tangent in geometry is defined as a line that touches the circle at only one point. The point of contact of the tangent with the circle is known as the point of tangency.
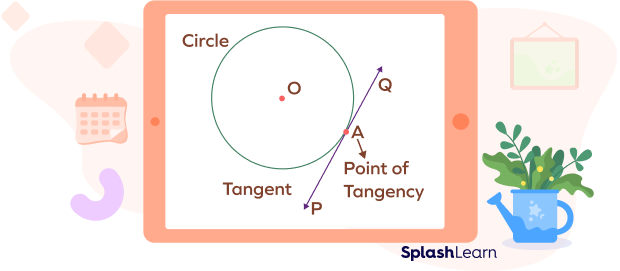
Here, the line PQ is the tangent to the circle with center O. The line PQ touches the circle at only one point, A.
The point A is the point of tangency.
Recommended Games
Tangent Properties
- A tangent touches a circle at only one point.
- A tangent is a straight line that never enters the interior of the circle.
- The tangent makes a right angle at the point of tangency with the radius of a circle.
- Tangents drawn from an external point to a circle have the same length.
- A circle can have infinitely many tangents.
- We can draw exactly one tangent to a circle passing through a point that lies on a circle.
- We can draw exactly two tangents to a circle passing through a point that lies outside the circle.
Recommended Worksheets
Tangent Theorems
There are some theorems based on the tangent of a circle, let’s discuss their statements and proof in detail.
Theorem 1: Tangent Radius Theorem
The tangent makes a right angle with the radius of a circle at the point of tangency.
(At the point of tangency, the tangent is perpendicular to the radius.)
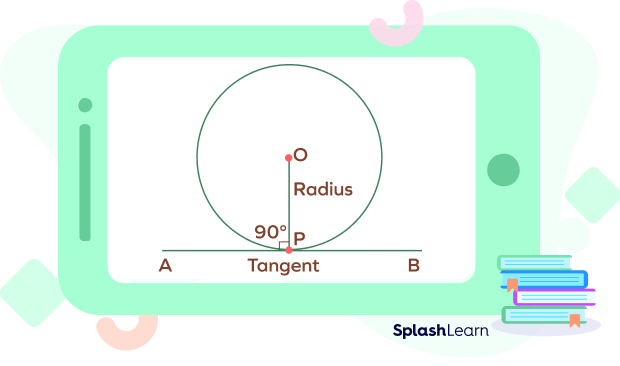
To prove: The radius OP is perpendicular to tangent AB.
Proof:
The points A and B lie outside the circle.
Thus, we can write
$OA \gt OP$
$OB \gt OP$
Thus, for any such point on the line AB, we will get the same relation.
It means that OP is the shortest distance between line AB and the point O.
Thus, $OP \bot AB$.
$\angle OPA = \angle OPB = 90^{\circ}$.
Theorem 2: Two Tangents Theorem
The lengths of two tangents from a common external point to a circle are equal. The two tangents will subtend equal angles at the center. The line that connects the exterior point to the center will divide the angle between the tangents into two equal angles.
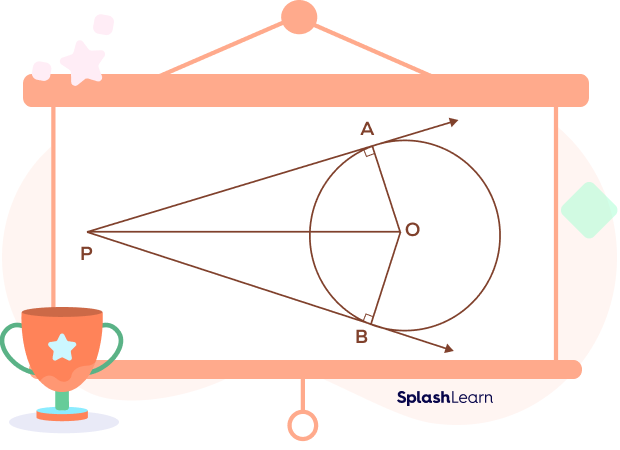
Let’s consider two tangent lines PA and PB are drawn from an external point “P” as shown in the figure, then
- $PA = PB$
- The two tangents subtend equal angles at the center of the circle. $\left[\angle POA = \angle POB\right]$
- The line that connects the exterior point to the center will divide the angle between the tangents into two equal angles. $\left[\angle OPA = \angle OPB\right]$
Tangent of a Circle: Formula
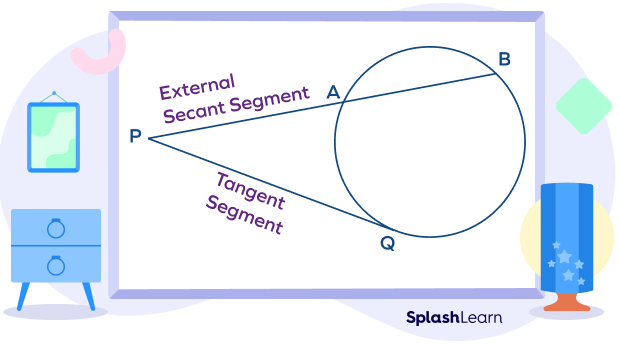
How can we find the tangent of a circle? The “tangent-secant theorem” explains the relationship between a tangent and a secant of the same circle.
Let’s consider a circle with P as any exterior point, PQ is a tangent, and AB is a secant drawn from external point P.
Here, PA is the external secant segment.
The formula for tangent-secant relationship is given by
$PQ^2 = PA \times PB$.
General Equation
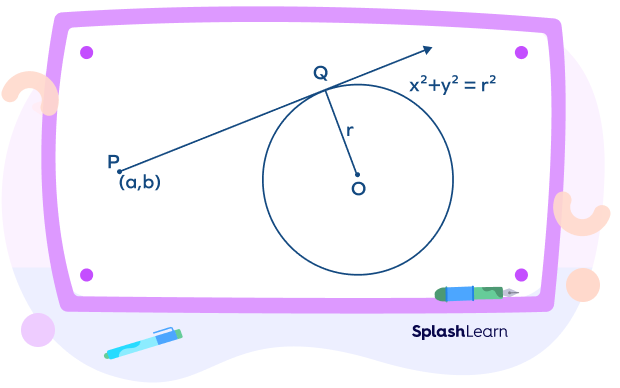
- If the equation of the circle is $x^2 + y^2 = r^2$, and a tangent is drawn from any external point (a, b) as shown in the figure below, then the general equation of the tangent to a circle is $xa + yb = r^2$.
- If the general equation of a line is y=mx+c and that of a circle is $x^2 + y^2 = r^2$, then the general equation of the tangent to the circle is given by $y = mx \pm r\sqrt{1+m2}$.
- The tangent to a circle equation $x^2 + y^2 = a^2$ at $(a\; cos\; \theta,\; a\; sin\; \theta)\; is\; x.\;cos\; \theta + y.\;sin\; theta = a$
- The tangent to a circle equation $x^2 + y^2 + 2gx + 2fy + c = 0$ at $(x_1,\; y_1)$ is
$xx_1 + yy_1+ g(x + x_1) + f(y + y,) + c = 0$
Condition of Tangency
When the distance between the center of the circle and the straight line is the same as the radius of the circle, then the given line will touch the circle.
There are exactly two tangents to circle from a point outside the circle. We can draw only one tangent to a circle through a point that lies on the circle. A tangent cannot be drawn from a point lying inside the circle.
Facts about Tangent of a Circle
- If a particle or object moves in a circular path, and we abruptly stop its motion, then it will move in a direction that is tangent to the circular path. That means the direction of velocity will be tangential to the circular path.
- Circle and tangent of a circle can be applied in our daily life, such as in construction, architecture, and engineering.
- Real-life example: When the wheels of a bicycle roll along a road, the roadline can be compared to a tangent to the wheel at each point.

Conclusion
In this article, we learned about the tangent of a circle, its properties, theorems, formula, general equations of tangents, condition of tangency, etc. Let’s solve a few examples and practice problems.
Solved Examples on Tangent of a Circle
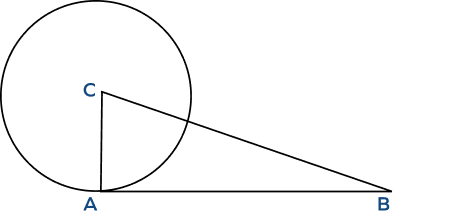
- In the given figure, if $AC = 15$ inches and $BC = 20$ inches, find the length of the tangent.
Solution:
$AC = 15$ inches and $BC = 25$ inches.
As we know, the radius and tangent of a circle are perpendicular to each other.
In ABC, applying Pythagoras’ theorem
$AC^2 + AB^2 = BC^2$
$15^2 + AB^2 = 25^2$
$AB^2 = 25^2 \;−\; 15^2$
$AB^2 = 25^2 \;−\; 15^2$
$AB^2 = 400$
$\therefore AB = 20$ inches.
- Find the value of “x” in the figure given below.
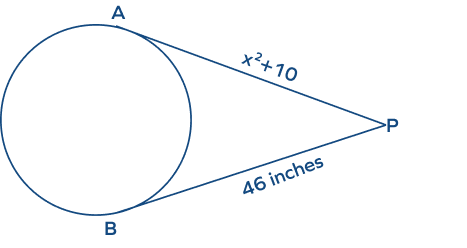
Solution:
Two tangent lines PA and PB are drawn from an external point “P.” Thus, the two tangents have the same length.
$PA = PB$.
Therefore,
$x^2 + 10 = 46$
$x^2 = 46 \;−\; 10$
$x^2 = 36$
$x = 6$
Hence, the value of “x” is 6.
- In the figure given below, if $PA = 9$ feet, $AB = 7$ feet, find the length of the tangent PQ.
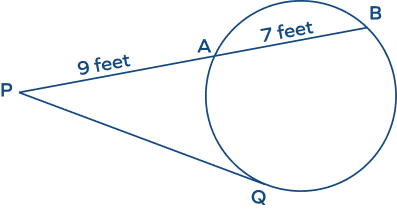
Solution:
Given, $PA = 9\; feet,\; AB = 7\; feet$
Here, $PB = PA + AB = 9\; feet + 7\; feet = 16\; feet$
According to the tangent-secant formula,
$PQ^2 = PA \times PB$
$PQ^2 = 9 \times 16$
$PQ^2 = 144$
$PQ = 12\; feet$
Hence, the length of tangent PQ is 12 feet.
- In the figure given below, if $DC = 14$ inches and $BC = 11$ inches, find the radius of the circle.
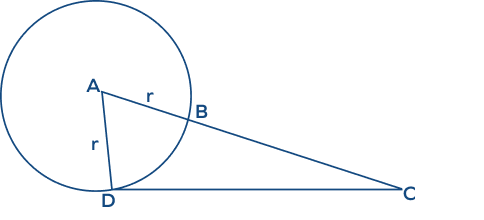
Solution:
Given, $DC = 14$ inches and $BC = 11$ inches
Here, $AC = AB + BC = r + 11$
According to the tangent-secant formula,
$DC^2 = BC \times AC$
$14^2 = 11 (r + 11)$
$196 = 11r + 121$
$11r = 196 \;−\; 121 = 75$
$r = \frac{75}{11} = 6.81$
Hence, the radius of the circle is 6.81 inches.
Practice Problems on Tangent of a Circle
Tangent of a Circle: Definition, Properties, Formula, Examples
A line that touches the circle at _____ is called a tangent to the circle.
A tangent to the circle touches the circle at only one point.
The number of tangents that pass through a point on a circle is _____.
Only one tangent can be drawn through a point on a circle.
How many tangents can be drawn from an external point to a circle?
From an external point, two tangent lines can be drawn to a circle.
Which of the following results is related to the figure given below?
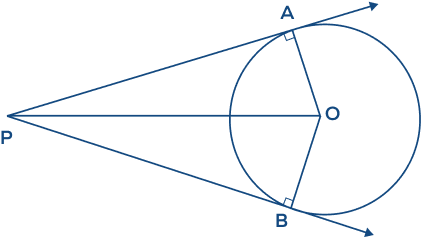
All results are given in options a, b, and c are about the “two tangent theorem,” which is shown in the given figure.
What is the length of tangent AP in the given figure?
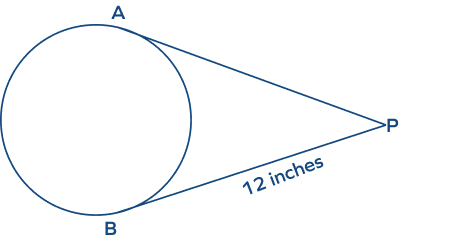
The lengths of two tangents from a common external point to a circle are equal.
Therefore, $AP = PB = 12\; inches$.
Frequently Asked Questions on Tangent of a Circle
What is the point of tangency of a circle?
The point of contact of the tangent with the circle is known as the circle’s point of tangency.
What are the two important theorems related to tangents to a circle?
The two important theorems related to tangents to a circle are as follows:
Theorem 1: The tangent makes a right angle at the point of tangency with the radius of a circle.
Theorem 2: The lengths of the two tangents drawn from an external point to a circle are equal.
What is the tangent-secant formula?
If P is the exterior point of a circle, PQ is a tangent and AB is a secant drawn from external point P, then the formula for tangent-secant is given by, $PQ^2 = PA \times PB$.
How many tangents are drawn from a point within the circle?
There is no way to make a tangent when a point is inside the circle. That means zero tangents are drawn from a point within a circle.
How many tangent lines are possible for a circle inscribed in a triangle?
When a circle is inscribed in a triangle then all three sides of the triangle become the circle’s tangent. Hence, three tangent lines are possible, i.e., an incircle of a triangle has three tangents.