Terminating Decimals – Definition, Theorem, Examples

What Is a Terminating Decimal?

A terminating decimal is a decimal in which the digits after the decimal point terminate. This means that the digits after the decimal are finite in number. It is a decimal that has an end-digit.

Terminating decimal examples: 17.28, 6.02, −22.45435, 0.45, etc.

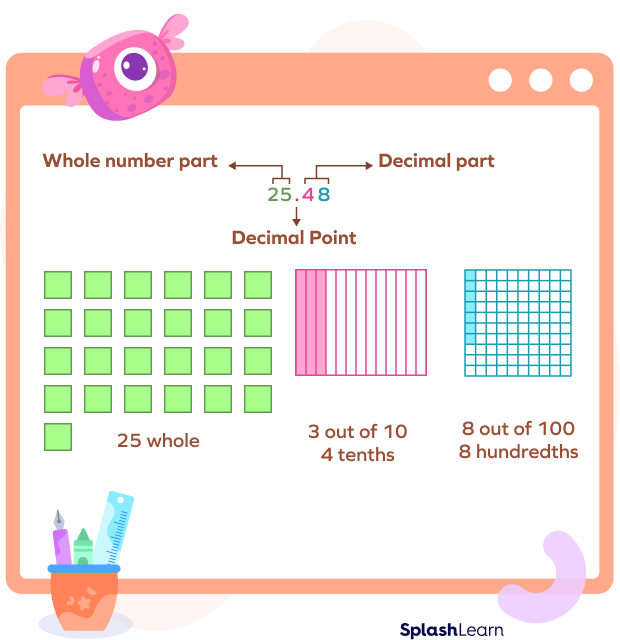
A decimal is a number that consists of a whole number and a fractional part. There are two types of decimals categorized on the basis of the number of digits after the decimal point.

• Terminating Decimals
• Non-terminating Decimals

Let’s consider an example of terminating decimals in real life. If you have two chocolates and you ate half of one of the chocolates, then you are left with 1.5 chocolate. This is a terminating decimal since there is only one digit after the decimal point.

Terminating Decimal Definition

Terminating decimals can be defined as decimals that have a finite number of digits after the decimal point.  

Example: 25.37 is a terminating decimal.

Note that all decimals that terminate are rational numbers. In simple words, all terminating decimals are rational numbers. Thus, they can be written in the form of a fraction, as they are rational numbers.

Example 1: 1.5 can also be written as $\frac{15}{10}$.

Example 2: $\frac{1}{8} = 0.125$

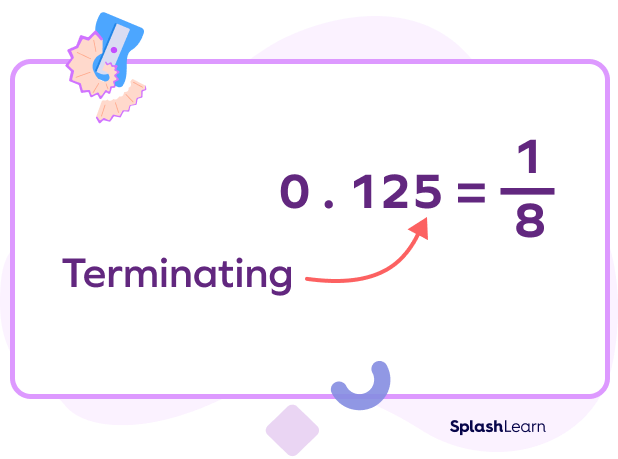
Let’s see the steps for the long division where we divide 1 by 8 to get the quotient as 0.125. Here, the long division ends after a certain point and we get the remainder 0.

How to Identify a Terminating Decimal

You can identify a terminating decimal number using the following conditions:

• It always has a finite number of digits after the decimal point.
• It is a rational number. 
• If the simplified form of a rational number has the denominator in the form of $2^m \times 5^n$, where m and n are positive integers, then it has a terminating decimal expansion.

Theorems on Terminating Decimals

1. If a rational number k has a terminating decimal expansion, then k can be expressed in the form $\frac{p}{q}$, such that $q \neq 0$, where p and q are co-prime and the prime factorization of q is of the form $2^m \times 5^n$, where m and n are non-negative integers.

Example:$ 0.5 = \frac{5}{10} = \frac{1}{2}$

2. If k $= \frac{p}{q}$ is a rational number, where q ≠ 0 is a rational number with prime factorization $2^m \times 5^n$, where m and n are non-negative integers, then k is a terminating decimal number.

Example: $\frac{7}{8}= \frac{7}{2^3} = 0.875$

What Is a Non-Terminating Decimal?

These numbers are called non-terminating decimals because the digits after the decimal point do not terminate. This means that the digits after the decimal are infinite in number. These are further divided into two categories:

• Recurring Non-terminating Decimal Numbers: In these decimal numbers, the digits after the decimal point are infinite as well as repeating. This means the digits after the decimal place digits follow a specific pattern. 

For example, $4.213213….= 4.213, 2.34343434….= 2.34, 1.9999999….= 1.9$, etc. 

In these examples, one or more than one digit after the decimal keeps repeating. 

• Non-recurring Non-terminating Decimal Numbers: In these decimal numbers, the digits after the decimal point are infinite as well as non-repeating. This means the digits after the decimal place digits don’t follow a specific pattern.

For example, 3.23447452…, 1.36098757…, 0.9374940…, etc.

Such decimals fall under the category of irrational numbers.

Let’s see the steps for long division where we divide 11 by 9. Here, the process of long division goes on. The remainder never becomes 0.

Facts Related to Terminating Decimals

• Pi $(\pi) = 3.14159…$ is a non-terminating and non-repeating decimal number. It is an irrational number. 
• Recurring decimal numbers can be written by putting a bar sign or dots over the digits repeating after the decimal point. Example: $1.66666….= 1.6$

Conclusion

Decimal numbers are of two types: terminating decimal numbers and non-terminating decimal numbers. Terminating decimals and non-terminating but recurring decimal numbers are called rational numbers and can be expressed as $\frac{P}{q}, q \neq 0$, $p$ and $q$ are integers. On the other hand, non-terminating and non-recurring decimals are called irrational numbers and cannot be expressed in the rational form. Let’s solve a few examples based on the concept of terminating decimals.

Solved Examples on Terminating Decimals

1. Out of the given fractions $\frac{7}{5}, \frac{5}{15}, \frac{7}{42}$, and $\frac{4}{10}$ , which one will result in a terminating decimal?

Solution: 

The fractions can be expressed as:

$\frac{7}{5} = 1.4$

$\frac{5}{15} = 0.333…$

$\frac{7}{42} = 1.666…$

$\frac{4}{10} = 0.4$

Therefore, the fraction resulting in terminating decimals are $\frac{4}{10}$ and $\frac{7}{5}$.

2. Is the decimal number 1.111 a terminating decimal?

Solution: 

Terminating decimal is a decimal that has an end-digit.

The decimal 1.111 is a terminating decimal since it has a finite number of digits after the decimal point. 

3. Any rational number with its denominator in the form of _______, where m and n are non-negative integers is a terminating decimal number.

Solution: 

Any rational number with its denominator in the form of $2^m \times 5^n$, where m and n are non-negative integers is a terminating decimal number, otherwise it is non-terminating.

4. Find out whether 5.348 is a terminating or a non-terminating decimal. 

Solution: 

The given decimal is 5.348.

Multiply and divide it by 1000, we get

$5.348 = \frac{5.348 \times 1000}{1000} = \frac{5348}{1000}$

It’s a terminating decimal because it can be expressed in the form of p/q. 

5. Is $\frac{4}{3}$ a terminating or a non-terminating decimal?

Solution: On dividing we get, $\frac{4}{3} = 1.333333…$ 

Which means it is a repeating decimal.

Practice Problems on Terminating Decimals

Frequently Asked Questions on Terminating Decimals