What Is a Period in Math?
The term “period” is used in different ways or contexts in mathematics such as period of a function, decimal periods, periods in place value chart, or period in context of time.
Period as a general term refers to the measurable portion of time. School hours are divided into periods, such that each period represents a certain time-interval in which you study a particular subject. It is used as a point to mark the end of an event in the cycle.
Recommended Games
Definition of Period in Math
We will define “period” in terms of different contexts.
Period of a function: Period of a function is the interval at which the function repeats itself. A function is said to be periodic with period $T\gt 0$ if $f(x + T) = f(x)$ for all $x$ in the domain of $f$.
Period of a Repeating Decimal: The recurring part (the recurring digit or the group of recurring digits) in a repeating decimal is called the period of the decimal.
Period in Place Value Chart: In the place value chart, when a number is written in standard form, each group of digits separated by a comma is called a period.
Period in terms of time: Period is defined as the measurable portion of time or completion of cycle.
Recommended Worksheets
Period of a Function
A periodic function is defined as a function that repeats its values at regular intervals or periods. Such functions return the same value at regular intervals. This regular interval is known as the period of the function.
A function $f(x)$ is said to be periodic with period $T$ if $f(x + T) = f(x)$, for $T \gt 0$. The least positive value of T is called the fundamental period.In trigonometry, you must have seen graphs in which functions repeat themselves. The length of one complete cycle of a trigonometric function is referred to as the period of the function. Look at the graph of the function sin x. You can see that the graph repeats itself after equal interval of 2. Thus, the period of the sine function is 2.
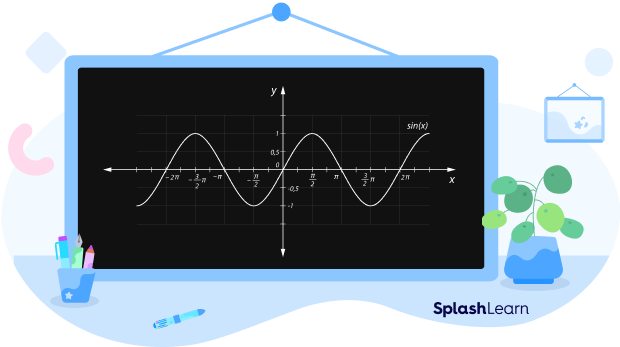
Period of Trigonometric Functions
| Function | Period |
|---|---|
| $sin\; x$ | $2\pi$ |
| $cos\; x$ | $2\pi$ |
| $tan\; x$ | $\pi$ |
| $cosec\; x$ | $2\pi$ |
| $sec\; x$ | $2\pi$ |
| $cot\; x$ | $\pi$ |
Period Formula: Period of a Function
$T = \frac{Period of parent function}{| Coefficient of x |}$
Example: Period of $sin\; 2x = T = \frac{2\pi}{2} = \pi$
Frequency $= F = \frac{1}{Period} = \frac{1}{T}$
Frequency refers to the number of times the graph of a function repeats itself in a given amount of time.
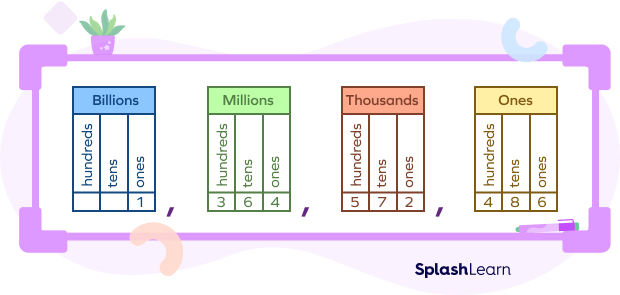
Periods in Place Value Chart
A period refers to a group of three digits in the place value chart separated by a comma when a number is written in the standard form. Periods help in understanding the place values of the digits. Place value is a numerical value that every digit in a number has based on its position. It can be extremely difficult to read big numbers without periods.
Here’s an example: 1,643,752,648 is much easier to read and understand than 1643752648.
In the International place-value system, there are four periods namely Ones, thousands, millions, and billions for the twelve places from right to left.
In the number 1,643,752,648, there are four periods. Each set with 3 digits makes 1 period.
Here’s another visual example:
| Billions | MIllions | Thousands | Ones | ||||||||
| HB | TB | B | HM | TM | M | HTh | TTh | Th | H | T | O |
| 1 | 6 | 4 | 3 | 7 | 5 | 2 | 6 | 4 | 8 | ||
Repeating or recurring decimals contain a digit or a group of digits that repeat endlessly and so, are called periodic. The digits in the repeating section are called its period. The number of repeating digits is called the length of period or the periodicity of the repeating decimal.
Examples of decimal periods:
- $\frac{1}{3} = 0.33333333… = 0.\\overline{3}$
Period of $\frac{1}{3} = 3$
Length of period $= 1$
- $\frac{41}{333} = 0.123123123… = 0.\overline{123}$
Period of $\frac{41}{333} = 123$
Length of period $= 3$
- $\frac{1}{7} = 0.142857142857…= 0.\overline{142857}$
Period of $\frac{1}{7} = 142857$
Length of period $= 6$
Facts about Period
- In the International place value chart, nine places are grouped into 3 periods – ones, thousands, and millions.
- In the Indian place value chart, nine places are grouped into 4 periods – ones, thousands, lakhs, and crores.
- A period (or full stop) is a punctuation mark in English represented by a small dot (.). It is used to express that a sentence is complete. It is also used in abbreviations.
Conclusion
In this article, we discussed the meaning of ‘period’ in math with respect to different contexts – period of a function, period in place values, decimal periods. Let’s solve a few examples for better understanding.
Solved Examples on Period
1. Find the period of $\frac{5}{6}$.
Solution:
Convert the fraction into decimal form.
$\frac{5}{6} = 0.833333333… = 0.8\overline{3}$
Period of $\frac{5}{6} = 3$
Length of period $= 1$
2. Find the period of 7 in 85,476,280.
Solution:
| MIllions | Thousands | Ones | ||||||
| Hundred Millions | Ten Millions | Millions | HundredThousands | TenThousands | Thousands | Hundreds | Tens | Ones |
| 8 | 5 | 4 | 7 | 6 | 2 | 8 | 0 | |
The digit 7 is placed in the thousands period.
Place value of 7 in $85,476,280 = 50,000$.
3. Find the period of $f(x) = cos(3x)$ if the period of $cos(x)$ is $2\pi$.
Solution:
The period of $cos(x)$ is $2\pi$.
The coefficient of x is 3.
Period of any function $f(x) = T = \frac{Period of parent function}{| Coefficient of x |}$Therefore, period of the given function $= \frac{2\pi}{3}$
Practice Problems on Period
Period in Math: Definition, Solved Examples, Facts, FAQs
What is the period of 1 in 87,356,180?
The digit 1 is placed at the hundreds place which is part of the Ones period.
How many digits are there in a period?
Three digits make up one period.
What is the period of tan x?
The period of tan $x$ is $\pi$.
What is the length of the period of repeating decimal 0.456456456456...
The length of the period is the number of repeating digits. Here, 456 is the period and the length of the period is 3.
What is the length of the period of repeating decimal 0.133333333 . . .?
The length of the period is the number of digits that repeat itself. Here “3” is the period and the length of the period is 1.
Frequently Asked Questions
How are periods shown in the international place value chart?
The international place value chart has three major periods – ones, thousands, and millions. Each period comprises three place values, namely ones, tens, and hundreds.
What is a period for a decimal number?
The recurring decimals have digits that repeat endlessly and so are called periodic. The digits that repeat are called its period and the number of digits that repeat is called the length of the period.
Can the period of a trigonometric function be negative?
No. Since the period refers to the length of the time-interval, it must always be positive.
What are the places included in the Ones period in math?
Ones period (units period) in math has three places – Ones, Tens, and Hundreds.
What does period mean in math?
The term “period” is used in different contexts such as period of a function, period of a repeating decimal, periods in place value chart, or period in context of time.




































