What Is Time Interval?
The amount of time between two given times is known as time interval. In other words, it is the amount of time that has passed between the beginning and end of the event. It is also known as elapsed time.
Let’s understand this concept with an example of time interval.
Example: Sam had soccer practice after school. Training started at 4:00 p.m. and ended at 5:00 p.m. For how long did he play?
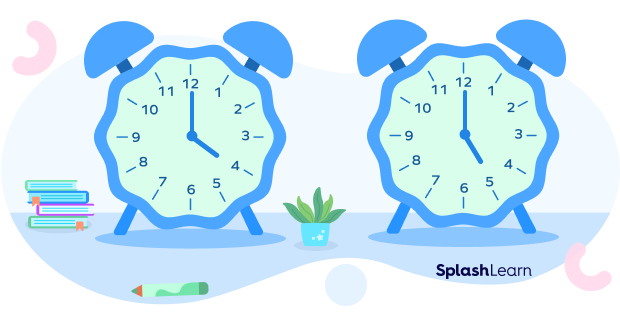
The interval between 4:00 p.m. and 5:00 p.m. is one hour. So, Sam played soccer for one hour.
Recommended Games
Units for Measuring Time
Interval of time is measured in different units. Each unit describes a different amount of time. Some units are better suited to specific intervals of time. For example, if you were baking a cake in the oven, you would choose to measure the time in minutes or maybe in hours. If you were calculating the time for your birthday from a specific date, you would prefer to measure the time in days, weeks, or months (depending on how far away it was).
The smallest unit of time used every day is a second.
 | 1 minute $= 60$ seconds 1 hour $= 60$ minutes24 hours $= 1$ day |
Seconds, minutes and hours can be calculated on a clock or watch. If we want to measure bigger time units, we prefer a calendar.
Seconds, minutes and hours can be calculated on a clock or watch. If we want to measure bigger time units, we prefer a calendar.
 | 1 week $= 7$ days1 month $= 30$ or 31 or 28 or 29 days (depending on the month and year)1 year $= 12$ months |
Also,
- 10 years $= 1$ decade
- 100 years $= 1$ century
- 1000 years $= 1$ millennium
Recommended Worksheets
Calculating Time Interval
By definition, time interval is the amount of time between two given times. We can calculate the time interval in math by determining the difference between the start and end times. We can show differences in time using a number line or by simply subtracting two different times.
Time Interval on the Number Line
We can calculate the elapsed time using number lines. To calculate, we divide the number line into equal intervals of time. Suppose you have to calculate the amount of time between 2:05 p.m and 2:35 p.m.
The first step would be to plot both the times on a number line:
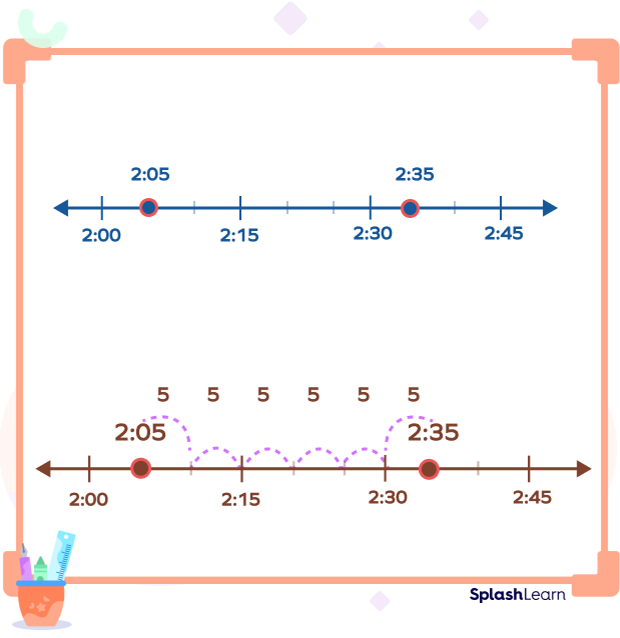
We can count the number of tick marks between the two times and multiply that by the value of each tick mark (5 minutes), as shown in the figure above. So, the answer is $6 \times 5$ minutes or 30 minutes.
Subtracting Times
We can calculate the amount of time between two events by finding the difference between the start and end times.
Time Interval $=$ Final Time – Starting Time
Here are the steps to subtract two times when both the times are either in a.m. or in p.m.
Step I: If the minutes of the first (end) time is less than the minutes of the second (start) time, then in the first (end) time,
- Take one hour away
- Add 60 to the minutes of the first time.
Step II: Subtract the minutes.
Step III: Subtract the hours.
Hence, the resultant from Step II and Step III together is the answer.
For example, calculate the time covered between 4:15 p.m. and 4:45 p.m.
4: 45 pm $-$ 4:15 pm
Step I: Here, the minutes of the first (end) time is not less than the minutes of the second (start) time. So, we move on to the next step.
Step II: Subtract the minutes. $45 – 15 = 30$
Step III: Subtract the hours. $4 – 4 = 0$
So, the final answer is 30 minutes.
Here’s another example: Calculate the time between 7:10 p.m. and 9:00 p.m.
9:00 – 7:10. Here, we will use regrouping.
Step I: Here, the minutes of the first (end) time is less than the minutes of the second (start) time. So, we borrow 1 hour and add 60 minutes.
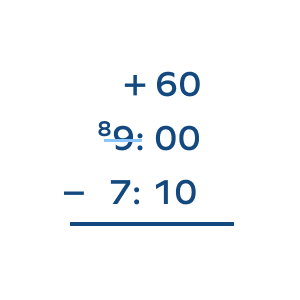
Step II: Subtract the minutes. $60 – 10 = 50$
Step III: Subtract the hours. $8 – 7 = 1$.
So, the solution is 1 hour and 50 minutes.
Let’s look at another example: Calculate the time interval between 8:45 a.m. and 2:30 p.m.
If one of the times is in a.m. and the other is in p.m., we will follow the below steps:
Step I: Find the time elapsed between 8:45 a.m. and 12 noon.
Between 8:45 a.m. and 12:00 noon, we have 3 hours and 15 minutes.
Step II: Find the amount of time between 12 noon and 2:30 p.m.
Between 12 noon and 2:30 p.m., the interval is 2 hours and 30 minutes.
Step III: Add the time of step I and step II to find the final answer.
3 hours and 15 minutes $+ 2$ hours and 30 minutes or 5 hours and 45 minutes
Conclusion
To conclude, as explained above, the amount of time between two given times. If you are looking for some more worksheets on the time, check out SplashLearn today! Visit the website to make learning a fun experience.
Solved Example
Example 1: Find the time interval between 17:20 and 18:50 on a number line.
Solution:
Method 1:
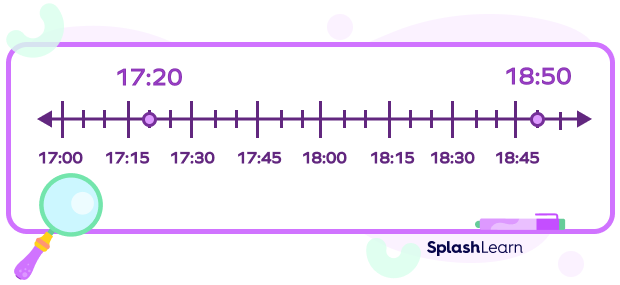
The number line is divided into equal intervals of 5 minutes.
Between the two points marked, there are 18 intervals.
Therefore, the amount of time between 17:20 and 18:50 is 185 or 90 minutes $= 1$ hour and 30 minutes
Method 2:
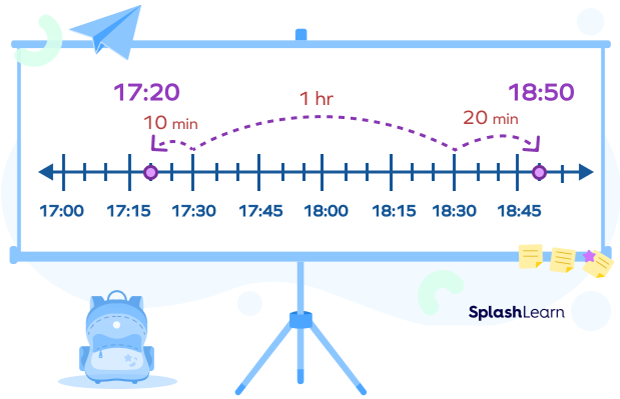
By looking at the number line, we get that between 17:20 and 18:50, we have 10 minutes $+ 1$ hour $+ 20$ minutes $= 1$ hour 30 minutes
Example 2: How many hours and minutes are there between 10:10 a.m. and 2:45 p.m.?
Solution:
Amount of time between 10:10 a.m. and 12 noon $= 1$ hour 50 minutes
Interval between 12 noon and 2:45 p.m. $= 2$ hours 45 minutes
So, the interval between 10:10 a.m. and 2:45 p.m.
$= 1$ hour 50 minutes $+ 2$ hours 45 minutes
$= 4$ hours 35 minutes
Example 3: Anna plans to watch her favorite movie, which starts at 2:30 p.m. The time interval is 2 hours 34 minutes. At what time will the movie end?
Solution:
The time the movie ends $= 2:30$ p.m. $+ 2$ hours 34 minutes.
Adding 2 hours to 2:30 p.m., we get 4:30 p.m.
Adding 34 minutes to 4:30 p.m., we get 5:04 p.m.
Practice Problems
Time Interval - Definition with Examples
What is the time interval between 1:30 p.m. and 9:10 p.m.?
7 hours 30 minutes $\underrightarrow{^\text{+7 hr}}$ 8:30 p.m. $\underrightarrow{^\text{+40 min}}$ 9:10 p.m.
So, the answer is 7 hours and 40 minutes.
On an analog clock, what is the time covered when the hour hand moves from the number 4 to 5?
It takes 1 hour for the hour hand to move from one number to the next consecutive number on a clock.
Sam started his journey and reached his destination in 7 hours. If he reached at 12:00 p.m., then at what time did he start for his destination?
Elapsed time $= 7$ hours and the end time $=$ 12:00 p.m.
Start time $=$ 12:00 p.m. $- 7$ hours $=$ 5:00 a.m.
Frequently Asked Questions
How can we calculate the time interval on the number line?
To calculate the interval of time on a number line, we divide the number line into equal intervals and then jump from the start time to the end time.
What are some examples of time intervals in our daily lives?
The following are some examples of interval of time:
- The time taken to finish a race.
- The time taken to bake a cake.
- The duration of the journey is covered by a bus and so on.
What do you mean by estimated time interval?
The estimated time interval is the time that will be required for an event (that has not occurred yet) that is yet to be completed. It is generally used for flight duration.




































