What Is the Union of Sets?
The union of a collection of sets is a set containing all the elements of individual sets. The union of two sets A and B is a new set denoted by $A\cup B$, which contains all the elements of the set A and all the elements of set B (without repetition).
Example: Find $A\cup B$ if $A = \left\{1, 2, 4, 6\right\}$ and $B = \left\{2, 3, 6, 7, 8, 9\right\}$.
The union of sets A and B has all the numbers of individual sets without repetition.
$A \cup B = \left\{1, 2, 3, 4, 6, 7, 8, 9\right\}$.
Recommended Games
Union of Sets: Definition
The union of two sets, denoted by $A \cup B$, is a set that contains elements that are in either set A or set B, or in both.
In simple words, the union of two sets contains all the distinct elements of both the sets.
The union of two or more sets is the smallest set containing all elements from individual sets. The definition of union in mathematics can be explained as an operation on two sets that results in a new set formed by combining all the elements of the given two sets.
Recommended Worksheets
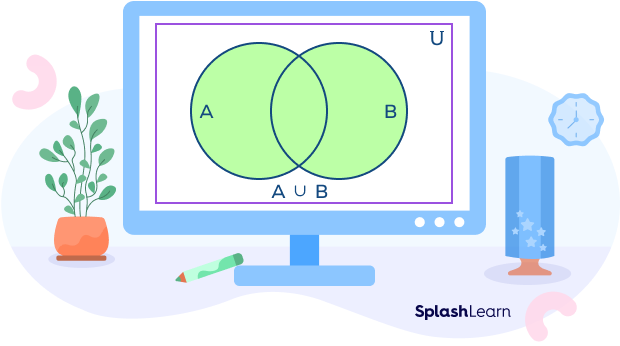
Venn Diagram of Union of Sets
Venn diagram is a visual representation or illustration that uses circles to show relationships between finite sets. Each circle represents a specific set. Any operation on sets can be represented using a venn diagram.
The union of sets is illustrated by the blue shaded region. It covers all the elements from both the sets. Here, U is a universal set, a big set such that A and B are subsets of U.
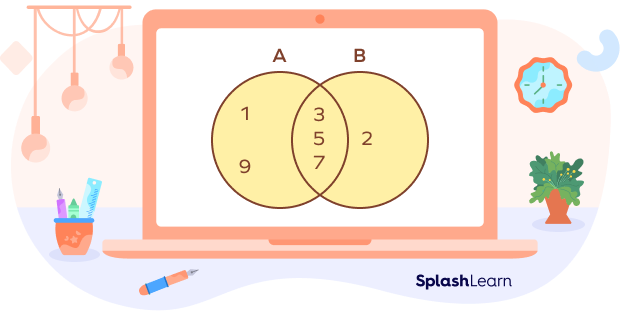
Example: Set $A = \left\{1, 3, 5, 7, 9\right\}$ and Set $B = \left\{2, 3, 5, 7\right\}$
$A \cup B = \left\{1, 2, 3, 5, 7, 9\right\}$
A Union B Notation
The union of two sets A and B is represented by writing the symbol “” between the two sets.
A union $B = A \cup B$
A Union B Formula
The formula of A union B or the formula for the union of two sets is given by
$A \cup B = \left\{ x: x \in A \text{or} x \in B\right\}$
Number of Elements in A Union B Formula
The number of elements in any set is called its cardinality. The generalized formula for the number of elements in the set “A union B” is:
$n(A \cup B) = n(A) + n(B) \;-\; n(A \cap B)$
Here,
n(A) is the cardinality of set A,
n(B) is the cardinality of set B, and
n(A B) is the number of elements present in the intersection of two sets.
Example: In a group, 20 people own a white car, 10 people own a black car, and 5 people own both a white and a black car. How many people own a white car or a black car?
$n(W) =$ Number of people who own a white car $= 20$
$n(B) =$ Number of people who own a black car $= 10$
$n(W \cap B) =$ Number of people who own a white and a black car $= 5$
$n(W \cup B) = n(W) + n(B) \;-\; n(W \cap B)$
$n(W \cup B) = 20 + 10 \;-\; 5$
$n(W\cup B) = 25$
25 people own a white car or a black car.
Properties of Union of Sets
The properties of the set union indicate their nature and help carry out further operations. Here are the five properties of the union of sets.
| Properties of Union | Notation |
|---|---|
| Commutative Property | $A \cup B = B \cup A$ |
| Associative Property | $(A\cup B)\cup C = A\cup (B\cup C)$ |
| Idempotent Property | $A \cup A = A$ |
| Property of Ⲫ/Identity Law | $A\cup \Phi = A$ |
| Property of Universal Set | $A\cup U = U$ |
- Commutative Property: $A \cup B = B \cup A$
The union sets will be independent of the order of the sets.
Example: set $A = \left\{\text{orange, banana, apple, mango}\right\}$ and set $B = \left\{1, 6, 2, 4\right\}$.
$A\cup B = \left\{\text{orange, banana, apple, mango,} 1, 6, 2, 4\right\}$
$B\cup A = \left\{\text{orange, banana, apple, mango,} 1, 6, 2, 4\right\}$
- Associative Property: $(A \cup B) \cup C = A \cup (B \cup C)$
The union of three or more sets does not depend on how we group the sets.
Example: Set $A = \left\{\text{orange, banana, apple, mango}\right\}$
Set $B = \left\{1, 6, 2, 4\right\}$
Set $C = \left\{\text{A, E, I, O, U}\right\}$.
$A \cup B = \left\{\text{orange, banana, apple, mango,} 1, 6, 2, 4\right\}$
$(A\cup B)\cup C = \left\{\text{orange, banana, apple, mango,} 1, 6, 2, 4, A, \text{E, I, O U}\right\}$
$(B\cup C) = \left\{1, 6, 2, 4, A, \text{E, I, O U}\right\}$
$A \cup (B \cup C) = \left\{\text{orange, banana, apple, mango,} 1, 6, 2, 4, \text{A, E, I, O U}\right\}$
Thus, $(A\cup B)\cup C = A\cup (B\cup C)$
- Idempotent Property: $A\cup A = A$
The property states that the union of the set with itself is the original set.
Example: $A = \left\{\text{orange, banana, apple, mango}\right\}$
$A\cup A = \left\{\text{orange, banana, apple, mango}\right\} \left\{\text{orange, banana, apple, mango}\right\}$
$A\cup A = \left\{\text{orange, banana, apple, mango}\right\}$
- Identity Law: $A\cup \phi = A$
The union of any set with a null set or empty set is the set itself. The null set is represented as . Thus, for any set A, we have $A\cup \phi = A$.
- Domination Property/Property of Universal Set: $A\cup U = U$
The union of a set with a universal set results in a universal set. The universal set contains all the elements of other sets.
Example: $A = \left\{1, 2, 3\right\}, U = \left\{1, 2, 3, 4, 5\right\}$
$A\cup U = \left\{1, 2, 3, 4, 5\right\} = U$
Facts about Union of Sets
- The complement of union of two sets is the intersection of the complements of the individual sets. This is known as De Morgan’s law.
$(A \cup B)’ = A’ \cap B’$ - $A \cup B$ is the event that consists of all sample points that are either in A or in B or in both A and B.
- Union of two sets is larger than the individual sets.
- The union of a set and the empty set is the original set.
Conclusion
Sets are clusters of numbers that can be acted upon through interesting operations. There are multiple types of sets, and the union of sets is one of the possible multiple operations. It refers to the collection of all the elements in individual subsets. The union of sets has distinguishing properties, making calculations quick and easy.
Solved Examples of Union of Sets
1. If $n(A) = 9, n(B) = 1, n(A\cap B) = 2$, what is the number of elements in A union B?
Solution:
$n(A\cup B) = n(A) + n(B) \;-\; n(A\cap B)$
$n(A\cup B) = 9 + 1 \;-\; 2$
$n(A\cup B) = 10 \;-\; 2$
$n(A\cup B) = 8$
2. What is the number of elements in the union of A and B, where $A = \left\{\text{x: x is a natural number and} 1 \lt x \le 6\right\},\; B = \left\{\text{x: x is a natural number and} 6 \lt x \lt 10\right\}$?
Solution:
$A = \left\{\text{x: x is a natural number and} 1 \lt x \le 6 \right\}$
Set $A = \left\{2, 3, 4, 5, 6\right\}$
$B = \left\{\text{x: x is a natural number and} 6 \lt x \lt 10\right\}$
Set $B = \left\{7, 8, 9\right\}$
Thus, $A\cup B = \left\{2, 3, 4, 5, 6, 7, 8, 9\right\}$
3. What is A B in the following venn diagram?
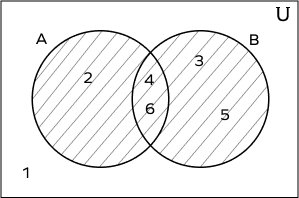
Solution:
$U = \left\{1, 2, 3, 4, 5, 6\right\}$
$A = \left\{2, 4, 6\right\}$
$B = \left\{3, 4, 5 ,6\right\}$
The entire shaded region represents $A\cup B$. Note that element 1 is not part of the union of A and B.
$A \cup B = \left\{2, 3, 4, 5, 6\right\}$
Practice Problems on Union of Sets
Union of Sets - Definition, Formula, Examples, Facts, FAQs
What is the union of set $A = \left\{\text{Parrot, Peacock, Sparrow}\right\}$ with the null set?
Union of any set with a null set is the set itself.
What is $A\cup A$?
By idempotent law, $A\cup A = A$.
If $A = \left\{0, 1\right\}$ and $B = \left\{1, 9\right\}$, then $A\cup B =$
$\left\{0, 1\right\}\;\left\{1, 9\right\} = \left\{0, 1, 9\right\}$
What is the union of A and B?
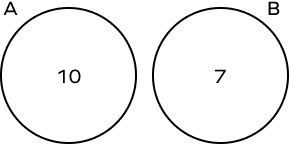
$A\cup B = \left\{10, 7\right\}$
The union of the set of natural numbers and the set {0} gives the set of _________.
The set of whole numbers include the set of natural numbers and 0.
Frequently Asked Questions about Union of Sets
What is the difference between union of sets and intersection of sets?
The union contains all the elements from each set, while the intersection contains only the common elements between the sets.
What is a complement of a set?
The complement of a set is a set containing all the elements in the universal set that do not belong to the given set.
What are disjoint sets?
Disjoint sets do not have any common elements. The union of such sets contains all the elements of individual sets, while intersection leads to empty or null sets.
Can the union of two sets be an empty set?
The union of two sets is empty when both sets are empty sets.



















