Unit Circle – Definition, Chart, Equation, Examples, Facts

What is a Unit Circle in Math?

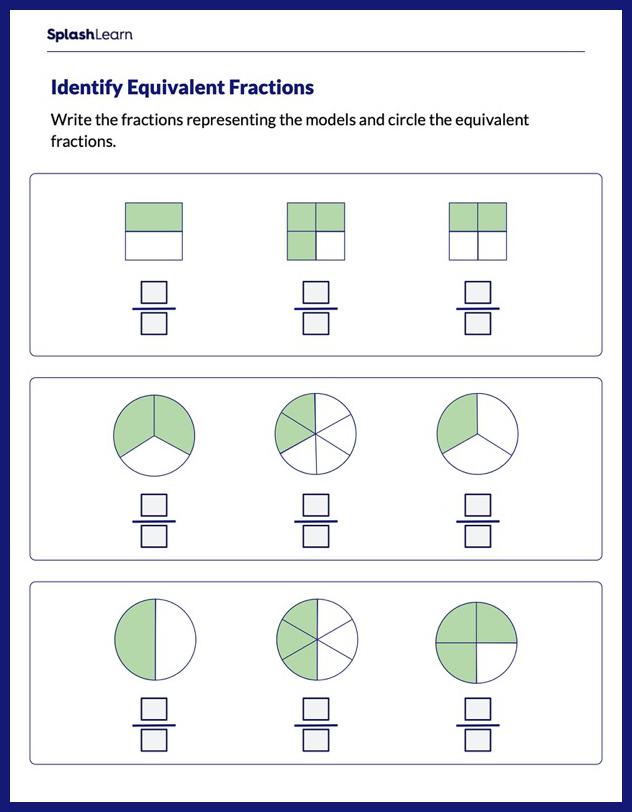
A unit circle is a circle of unit radius with center at origin. A circle is a closed geometric figure such that all the points on its boundary are at equal distance from its center. For a unit circle, this distance is 1 unit, or the radius is 1 unit. 

Let us learn the equation of the unit circle, and understand the ways to represent each of the points on the circumference of the unit circle, with the help of T-ratios.

Unit Circle: Definition

The unit circle is a circle with a radius of one unit.

The unit circle is fundamentally related to the concepts of trigonometry. The trigonometric functions can be defined using the unit circle.

A unit circle on the Cartesian plane is shown below. It has its center at origin and all the points on the circumference are at a distance of 1 unit from the center.

Equation of a Unit Circle

The general equation of a circle is of the form $(x \;-\; a)^2 + (y \;-\; b)^2 = r^2$, where the center of the circle is (a, b) and the radius is r. A unit circle in the x-y plane is formed with a center at origin (0,0) and radius 1. 

Thus, the equation $(x \;-\; a)^2 + (y \;-\; b)^2 = r^2$ becomes

 $(x \;-\; 0)^2 + (y \;-\; 0)^2 = 1^2$

$ x^2 + y^2 = 1$

Thus, the equation of the unit circle on an x-y plane is $x^2 + y^2 = 1$.

Finding Trigonometric Functions Using a Unit Circle

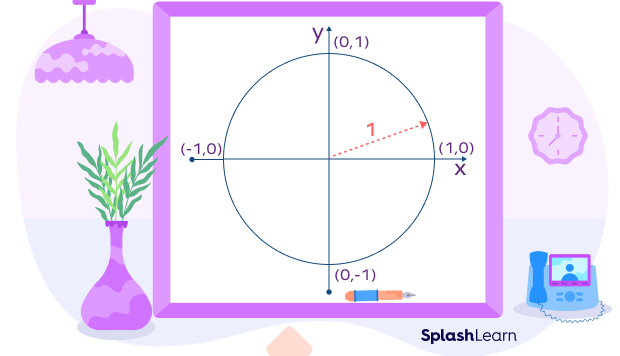
We can find trigonometric ratios using the unit circle. Consider the right triangle constructed in the unit circle shown in the diagram below. 

Let P(x,y) be any point on the circle such that the line joining the origin and the point P makes angle with the positive x-axis. The radius of the circle (length = 1 unit) represents the hypotenuse of the right triangle. So, the sides of the right triangle are 1, x, y.

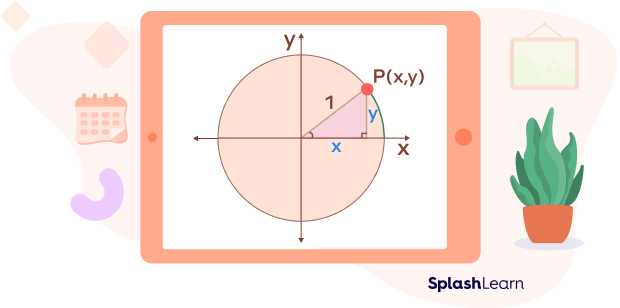
By the definition of the trigonometric ratios, we have

$sin\; \theta = \frac{Opposite\; Side}{Hypotenuse} = \frac{y}{1}$  

$\Rightarrow y = sin\theta$

$cos\; \theta = \frac{Adjacent\; Side}{Hypotenuse} = \frac{x}{1}$

$\Rightarrow x = cos\theta$

Thus, $P(x,y) = P(cos\theta ,\; sin\theta )$

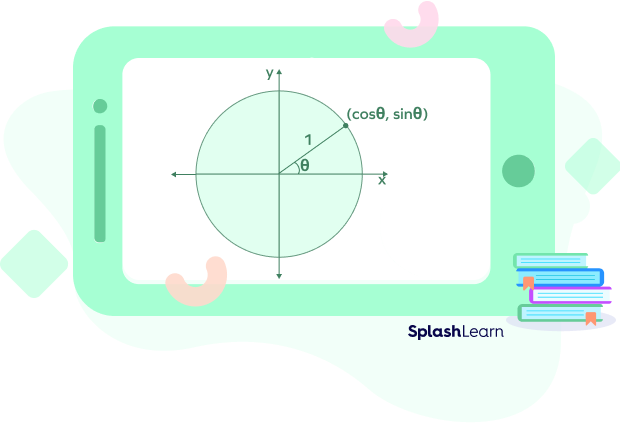
Unit Circle with Sin, Cos, and Tan

We just learnt that coordinates of any point on the unit circle are equal to $(cos\; \theta,\; sin\; \theta )$.

Thus, $x = cos\; \theta$ and $y = sin\; \theta$

Using these values, we can further calculate $tan\; \theta = \frac{sin\; \theta}{cos\; \theta}$

Example: Find the value of tan $60^\circ$ using sin and cos values from the unit circle.

We know that, tan$ \;60^{\circ} = \frac{sin\; 60^\circ}{cos\; 60^\circ}$

Refer to the unit circle chart. We get the values

$sin\; 60^\circ = \frac{1}{2}$

$cos\; 60^\circ = \frac{\sqrt{3}}{2}$

Therefore, tan $60^\circ = \frac{1}{2}\frac{\sqrt{3}}{2}$

tan $60^\circ = \frac{1}{3}$

Unit Circle and Trigonometric Values

The unit circle can be used to find all the trigonometric values. Let’s see some examples.

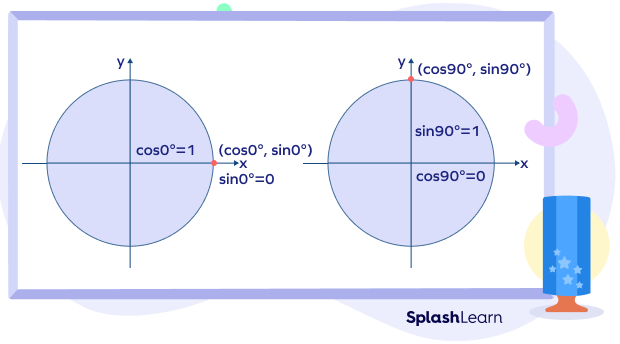
When $\theta = 0^\circ$, we have $x = 1$ and $y = 0$.

Thus,

$x = cos\; \theta = cos\; 0^\circ = 1$

and 

$y = sin\; \theta = sin\; 0^ \circ = 0$

Similarly, for $= 45^\circ$

$x = cos\; 45^\circ = \frac{1}{\sqrt{2}}$ and $y = sin\; 45^\circ = \frac{1}{\sqrt{2}}$.

If a right triangle is placed in a unit circle in the cartesian coordinate plane, with hypotenuse, base, and altitude measuring 1, x, y units respectively, then the unit circle identities can be given as,

• $sin\;(\theta) = y$
• $cos\;(\theta) = x$
• $tan\;(\\theta) = \frac{sin\; \theta}{cos\; \theta} = \frac{y}{x}$
• $sec\;(\theta) = \frac{1}{x}$
• $cosec\;(\theta) = \frac{1}{y}$
• $cot\;(\theta = \frac{cos\; \theta}{sin\; \theta} = \frac{x}{y}$

In the next section, we will look at the unit circle with radians and unit circle degrees.

Unit Circle and Pythagorean Identities

Let us observe how we derive these unit circle equations considering a unit circle. 

A point on the unit circle can be represented by the coordinates $cos\; \theta$ and $sin\; \theta$ .

Here, $x = cos\; \theta,\; $y = sin\; \theta$.

• The sides of the right triangle in the unit circle have the values of $sin\; \theta$ and $cos\; \theta$.

Applying the Pythagorean theorem, we can write $x^2 + y^2 = 1$

Substitute x and y, we get-

$sin^2\; \theta + cos^2 \;\theta = 1$

This equation is known as Pythagorean Identity.

It is true for all the values of $\theta$ in the unit circle.

• Using this first Pythagorean Identity, we can find the rest of the Pythagorean Identities.

$sin^2\; \theta + cos^2\; \theta = 1$

Dividing each term by $cos^2 \theta$

$\frac{sin^2\;\theta}{cos^2\;\theta} + \frac{cos^2\;\theta}{cos^2\;\theta} = \frac{1}{cos^2\;\theta}$

$tan^2\; \theta + 1 = sec^2\;\theta$

This is the second Pythagorean Identity.

• Now, on dividing each term of first equation by $sin^2\; \theta$, we get

$\frac{sin^2\; \theta}{sin^2\;\theta} + \frac{cos^2\;\theta}{sin^2\;\theta} = \frac{1}{sin^2\;\theta}$

$1 + cot^2\; \theta = cosec^2\theta$

This is the third Pythagorean Identity.

Unit Circle Chart in Radians and Degrees

The unit circle chart in radians is given in the diagram below. It represents a total angle of 2 radians or 360. 

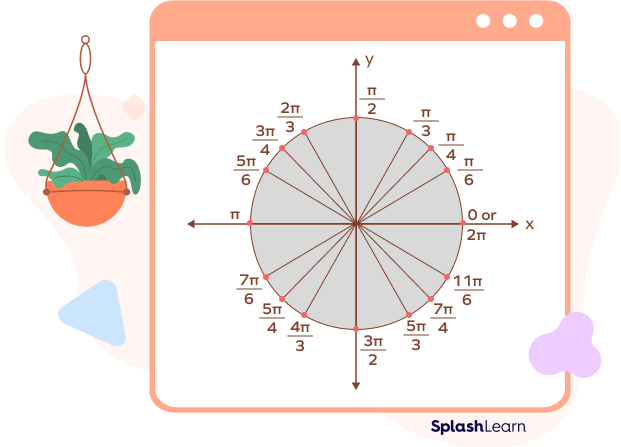
The unit circle is divided into four quadrants by the intersection of x-axis and y-axis. The points which represent the angles $\frac{\pi}{0},\; \frac{\pi}{6},\; \frac{\pi}{4},\; \frac{\pi}{3},\; \frac{\pi}{2}$ are the standard values of the trigonometric cosine and sine ratios.

The diagram shows unit circle values in both radians and degrees.

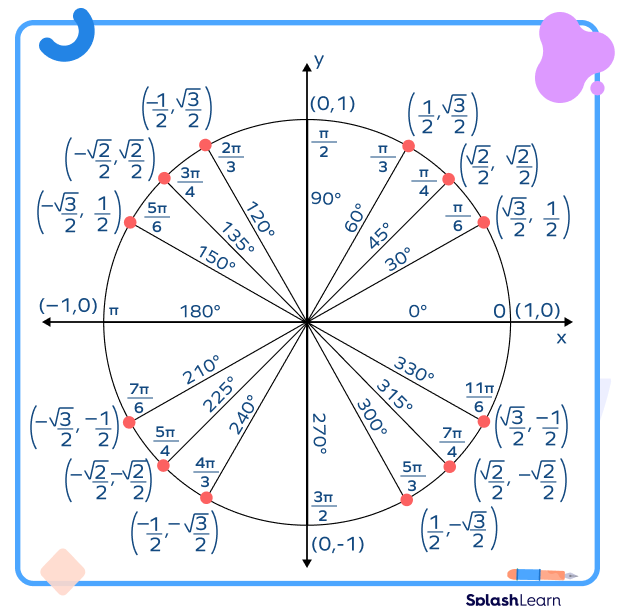
Unit Circle and Trigonometric Values

The unit circle can be used to find the various trigonometric identities and their principal angle values. Let’s see some examples.

When $= \theta\; 0^\circ$, we have $x = 1$ and $y = 0$.

$x = cos\; \theta = cos\; 0^\circ = 1$ 

$y = sin\; \theta = sin\; 0^\circ = 0$

Similarly, for $\theta = 45^\circ$

$x = cos 45^\circ = \frac{1}{\sqrt{2}}$ and $y = sin\; 45^ = \frac{1}{\sqrt{2}}$.

Let us now look at another angle of $90^\circ$.

Here, the value of cos $90^\circ = 1$, and sin $90^\circ = 1$. 

Unit Circle Table

The unit circle table helps to list the coordinates of the points on the unit circle and corresponding common angles using trigonometric ratios.

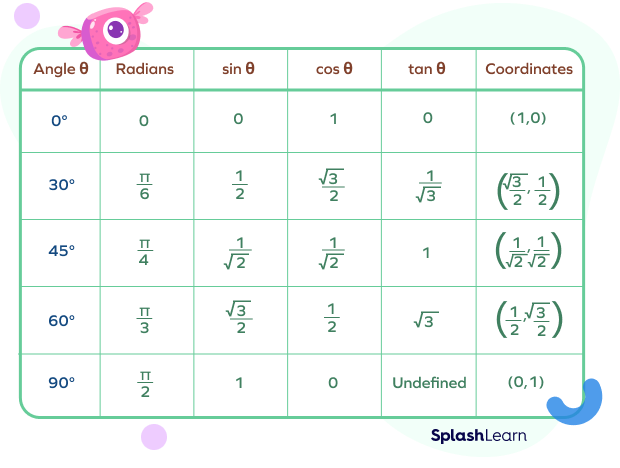
The table above can be used as a unit circle calculator. We can find the rest of the ratios, namely secant, cosecant, and cotangent functions using the given formulas:

$sec\; \theta  = \frac{1}{cos\; \theta}$

$cosec\; \theta = \frac{1}{sin\; \theta}$  

$cot\; \theta  = \frac{1}{sin\; \theta}$

Conclusion

In this article, we discussed unit circle and its properties. We saw some properties of trigonometry. And along with the concept of trigonometry, we solved T-ratios. We studied the unit circle chart. We solved many problems related to it.

Solved Examples on Unit Circle

1. Does the point A $( \frac{1}{4},\; \frac{1}{4})$ lie on the unit circle?

Solution:

We know that equation of a unit circle is:

$x^2 + y^2 = 1$

Substituting $x = \frac{1}{4}$  and $y = \frac{1}{4}$ , we get:

$= x^2 + y^2$

$= \frac{1^2}{4} + \frac{1^2}{4}$

$= \frac{1}{16} + \frac{1}{16}$

$= \frac{2}{16}$

$= \frac{1}{8}$

$\neq 1$

Since, $x^2 + y^2 \neq 1$ , the point A $(\frac{1}{4},\;\frac{1}{4})$ does not lie on the unit circle.

2. Does the point A $(\frac{1}{8},\; \frac{1}{8})$ lie on the unit circle?

Solution:

We know that equation of a unit circle is:

$x^2 + y^2 = 1$

Substituting $x = \frac{1}{8}$  and $y = \frac{1}{8}$ , we get:

$= x^2 + y^2$

$= \frac{1^2}{8} + \frac{1^2}{8}$

$= \frac{1}{64} + \frac{1}{64}$

$= \frac{2}{64}$

$= \frac{1}{32}$

$\neq 1$

 Since, $x^2 + y^2 \neq 1$ , the point A $(\frac{1}{8},\; \frac{1}{8})$ does not lie on the unit circle.

3. If $sin\; \theta + cos\; \theta = \frac{2}{3}$, what is $sin\; \theta.\; cos\; \theta$?

Solution: 

Given $(sin\; \theta + cos\; \theta) = \frac{2}{3}$  

Squaring both sides,

$(sin\; \theta + cos\; \theta)^2 = (\frac{2}{3})^2$

$sin^2\;\theta + cos^2\; \theta + 2\; sin\; \theta\; cos \theta = \frac{4}{9}$

$1 + 2\; sin\; \theta\; cos\; \theta = \frac{4}{9}$

$2\; sin\; \theta\; cos\; \theta = (\frac{4}{9}) \;-\; 1 = \frac{- 5}{9}$

$sin\; \theta\; cos\; \theta = \frac{-5}{18}$

4.  If $sin\; \theta = \frac{4}{5}$, find the value of $cos\; \theta$.

Solution:

Here, we use the identity $sin^2\; \theta + cos^2\; \theta = 1$

$(\frac{4}{5})^2 + cos^2\; \theta = 1$

$cos\; \theta = \sqrt{1\;-\; (\frac{4}{5})^2} = \sqrt{\frac{9}{25} = \frac{3}{5}}$

5. What is the area of a unit circle?

Solution:

The unit circle has radius $= 1$ unit. 

$Area = \pi r^2$

$Area = \pi\; square\; units$

Practice Problems on Unit Circle

Frequently Asked Questions on Unit Circle