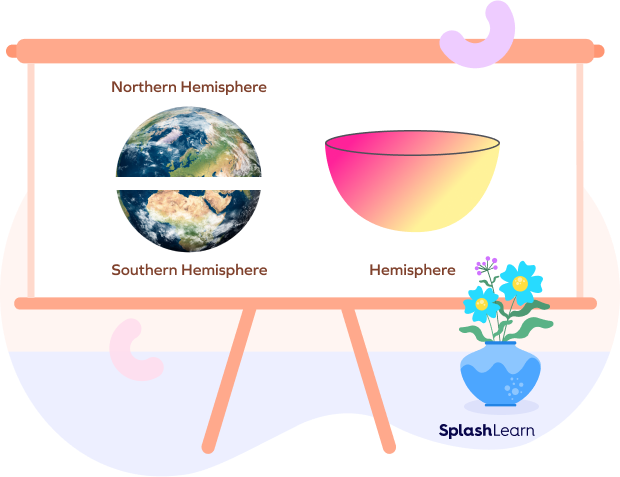
What is a Hemisphere?
The prefix “hemi” has a Greek origin and it means “half.” Thus, a hemisphere simply refers to the half of the sphere. If a sphere is divided into two equal parts, we will get two hemispheres.
You may have come across the word hemisphere in the real life context of planet Earth. For example, if you cut the Earth right on its equator, you’d have two halves: the northern and southern hemispheres.
Hemisphere: Definition
In geometry, the hemisphere is a 3D solid figure that is exactly half of the sphere. When a sphere is cut into two equal parts at the center then the hemisphere is formed. It has 1 flat circular base and 1 curved surface.
Recommended Games
Hemisphere Volume: Formula
The volume of a hemisphere is the total capacity of the hemisphere. The volume of hemisphere is measured in terms of cubic units, such as $in^3,\; ft^3$, etc.
The volume of sphere is calculated using the formula $V = \frac{4}{3} \pi r^3$.
So, what is the volume of a hemisphere?
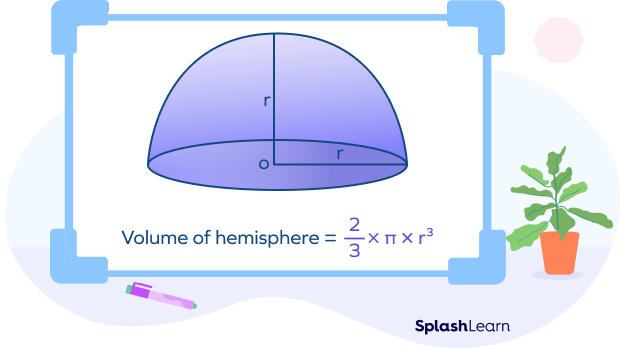
We know the hemisphere is simply half of the sphere. The volume of the hemisphere is also half the volume of the sphere.
Thus, the formula for volume of a hemisphere $= \frac{2}{3} \pi r^3$
How to Find the Volume of a Hemisphere
The volume is the amount of space that a 3D shape takes up.
Let us recall the formula of the volume of the hemisphere first.
Volume of Hemisphere $= \frac{2}{3} \pi r^3$
Here, the symbol stands for pi. We use the value of as 3.14 or $\frac{22}{7}$.
The r stands for radius, and it is the distance from the center point of the sphere.
We simply have to put the values in the above formula and find the volume of the hemisphere.
Facts about Volume of Hemisphere
- A hemisphere consists of only one curved surface area.
- The volume of the hemisphere is given as $\frac{2}{3} \pi r^3$ cubic units, where “r” is the radius of the hemisphere and is equal to $\frac{22}{7}$ or 3.14 approximately.
- A hemisphere has two surface areas, i.e., curved surface area and the total surface area. The curved surface area of a hemisphere is only the area covered by the curved surface, while the surface area of a hemisphere is the sum of the curved surface area and the base area of the hemisphere.
- As volume is a 3D concept including length, width, and height, volume of the hemisphere is measured in cubic units.
- The spherical coordinates of the hemisphere are $x = r \; cos \theta sin\; \Phi ,\; y = r sin \theta cos\; \Phi$, and $z = r\; cos\; \Phi$.
- Hemisphere Equation
When the radius “R” is centered at the origin, the equation of hemisphere is given by
$x^2 + y^2 + z^2 = R^2$
The Cartesian form or equation of a hemisphere with the radius “R” at the point $(x_0,\; y_0,\; z_0)$ is written as follows:
$(x\;-\;x_0)^2 + (y\;-\;y_0)^2 + (z\;-\;z_0)^2 = R^2$
The spherical coordinates of the hemisphere are given as follows:
$x = r\; cos\; \theta sin\; \Phi$
$y = r\; sin\; \theta cos\; \Phi$
$z = r\; cos\; \Phi$
Conclusion
The volume of a hemisphere is the total capacity of the hemisphere. In this article, we learnt in detail about the volume of the hemisphere formula, definition, and facts. Let’s solve some examples and practice problems to understand the concept better.
Solved Examples on the Volume of a Hemisphere
1. The diameter of a hemisphere is 6 ft. Calculate the volume.
Solution:
Given data,
Diameter of hemisphere $= 6$ ft.
Radius of hemisphere $= 3$ ft.
We know that, volume of hemisphere $= \frac{2}{3} \pi r^3$
$= \frac{2}{3} \times 3.14 \times 3^3$
$= \frac{2}{3} \times 3.14 \times 27$
$= 2 \times 3.14 \times 9$
$= 56.52\; ft^3$
The volume of the hemisphere is $56.52\; ft^3$.
2. A hemispherical bowl has an inner radius of 4 inches. How much water can it contain?
Solution:
Radius of hemispherical bowl $= 4$ in.
We know that, volume of hemisphere $= \frac{2}{3} \pi r^3$
$= \frac{2}{3} \times 3.14 \times 4^3$
$= \frac{2}{3} \times 3.14 \times 64$
$= \frac{401.92}{3}$
$= 133.97\; in^3$
Thus, the hemispherical bowl can contain $133.97\; in^3$ of water.
3. Find the radius of the hemispherical bowl if the area of its base is 154 unit square. $( \pi = \frac{22}{7})$
Solution:
Area of the base $= 154$ unit square.
We know that the area of the base of the hemisphere $= \pi r^2$
So, substituting value in the above formula the equation becomes:
$154 = \frac{22}{7} \times r^2$
$r^2 = 154 \times \frac{7}{22}$
$r^2 = \frac{1078}{22}$
$r^2 = 49$
$r = \sqrt{49}$
$r = 7$ units.
The radius of the hemispherical bowl is 7 units.
4. Find the volume of the hemisphere when its area of the circular base is 616 sq. units.
Solution:
Given data:
Area of circular base $= 616$ sq.units.
We know that:
The formula for the area of the circular base $= \pi r^2$
So, substituting value in the above formula the equation becomes,
$616 = \frac{22}{7} \times r^2$
$r^2 = 616 \times \frac{7}{22}$
$r^2 = \frac{4312}{22}$
$r^2 = 196$
$r = \sqrt{196}$
$r = 14$ units.
Thus, the volume of the hemisphere equation can be written as
Volume of hemisphere $= \frac{2}{3} \pi r^3$
$= \frac{2}{3} \times 3.14 \times 14^3$
$ = \frac{2}{3} \times 3.14 \times 2744$
$= \frac{17232.32}{3}$
$= 5744.10\; unit^3$
The volume of the hemisphere is $5744.10\; unit^3$.
5. A sphere with a radius of 5 inches is divided into two equal halves. Calculate the volume of each produced hemisphere.
Solution:
Given data,
Radius of sphere $= 5$ inch.
We know that the sphere and hemisphere have the same radius.
Thus, radius of hemisphere $= 5$ inch
Volume of each hemisphere $= V = \frac{2}{3} \pi r^3$
$= \frac{2}{3} \times 3.14 \times 5^3$
$= \frac{2}{3} \times 3.14 \times 125$
$= \frac{785}{3}$
$= 261.66\; in^3$
The volume of each hemisphere is $261.66\; in^3$
Practice Problems on the Volume of a Hemisphere
Volume of Hemisphere: Definition, Formula, Examples
The hemisphere is __________ of the sphere.
The prefix hemi means “half.” Thus, a hemisphere is simply half of the sphere.
The volume of the hemisphere is calculated using the formula __________.
$\pi r^2$ is the formula for the area of the circle. $\frac{4}{3} \pi r^3$ is the formula to derive the volume of the sphere. The volume of the hemisphere is half the volume of the sphere. So, the volume of the hemisphere is $\frac{2}{3} \pi r^3$.
The Cartesian form or equation of a hemisphere with the radius “R” at the point $(x_0,\; y_0,\; z_0)$ is written as __________.
The Cartesian form or equation of a hemisphere with the radius “R” at the point $(x_0,\; y_0,\; z_0)$ is written as $(x\;-\;x_0 )^2 + (y\;-\;y_0) 2 + (z\;-\;z_0 )^2 = R^2$
Which of the following statements about hemispheres is NOT TRUE ?
Hemisphere is a 3D figure.
Frequently Asked Questions on the Volume of a Hemisphere
What are some real-life examples of a hemisphere?
The examples of hemispheres can be seen in everyday life. Some examples are as follows:
- An igloo: The top of the igloo makes up the curved face of the hemisphere, while the base forms its flat face.
- Bowl: If you look at the bowl kept in the utensil cabinet of your kitchen, you can easily observe the hemisphere geometric shape.
- Fruits: If you cut a lemon or an orange exactly in half, you will get two hemispheres.

What are the differences between a circle and a sphere?
Circle: A circle is a 2D shape. It refers to a closed curved line. A circle does not have any volume.
Sphere: A sphere has a 3D shape. It is a round object. A sphere has volume.
How do you find the base area of a hemisphere?
The base of the hemisphere is in a circular shape, and therefore, the formula for the base area of the hemisphere is equal to the area of a circle.Thus, the base area of a hemisphere $= \p r^2$
What is the difference between the curved surface area of a hemisphere and the total surface area of a hemisphere?
Take a look at the image given below:
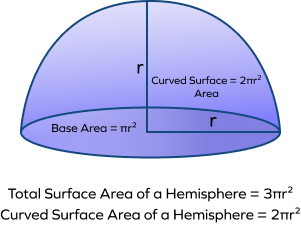
The curved surface area of the hemisphere is only the area covered by the curved surface. The formula for curved surface area of hemisphere is $2\pi r^2$. While the surface area of a hemisphere is the sum of the curved surface area and the base area of the hemisphere.
Thus, the total surface area of hemisphere $= 2 \pi r^2 + \pi r^2 = 3\pi r^2$
What is a polyhedron? Is the hemisphere a polyhedron?
A three-dimensional shape with flat polygonal faces, straight edges, and sharp corners or vertices is called a polyhedron. Common examples are cubes, prisms, pyramids. A hemisphere is not made up of polygons, so it is not a polyhedron.
























