Volume of a Pyramid

Volume of a Pyramid: Introduction

The volume of a pyramid is the space enclosed between all its faces.

A pyramid is a three-dimensional structure having a polygon as its base. All the side faces of a pyramid are triangles where one side of each triangle merges with a side of the base. Every corner of this structure is linked to a single point at the top, called apex, which makes it appear as a distinct shape. 

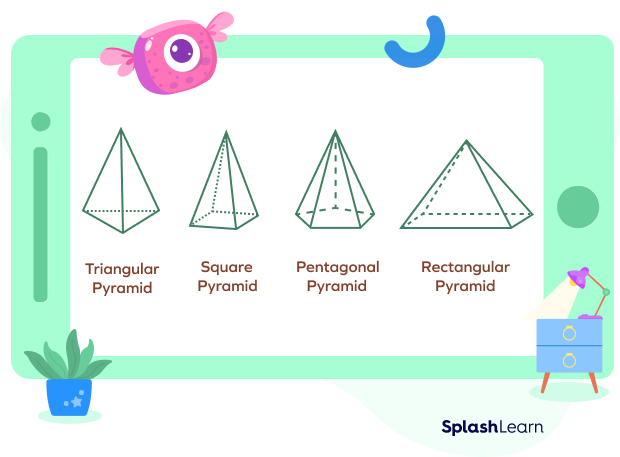
A pyramid is a polyhedron since its faces are made up of polygons. We have different types of pyramids that are named after their base, such as:

• Triangular pyramid: the base of a pyramid is a triangle
• Square pyramid: the base of a pyramid is a square
• Rectangular pyramid: the base of a pyramid is a rectangle
• Pentagonal pyramid: the base of a pyramid is a pentagon
• Hexagonal pyramid: the base of a pyramid is a hexagon

What Is the Volume of a Pyramid in Math?

The volume of a pyramid means the space enclosed within the pyramid by its faces. Volume is measured in cubic units such as $\text{ft}^{3}, \text{cm}^{3}, \text{m}^{3}, \text{in}^{3}$, etc. 

If the base area of the pyramid is A and the height is h, then the volume is given by 

Volume of a pyramid $= \frac{1}{3} \times A \times h$

A rectangular pyramid with dimensions l, w, h is shown below.

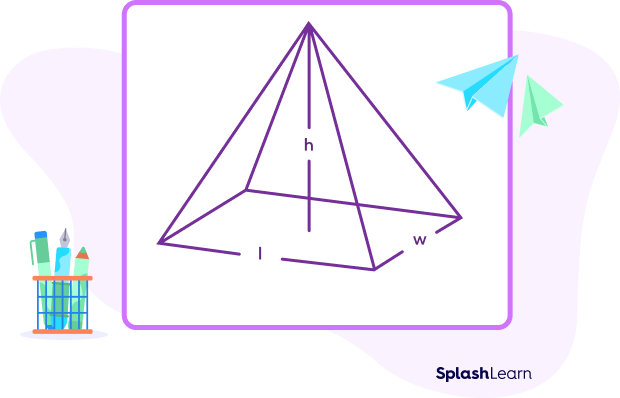
Its base is rectangular. So, the base area refers to the area of the rectangle.

Volume of the given rectangular pyramid $= \frac{1}{3} \times A \times h = \frac{1}{3} \times \text{lwh}$

Volume of a Pyramid: Definition

The volume of the pyramid is simply just one-third of the product of the base area and its height. It can also be defined as the number of unit cubes that can be fit into a pyramid. 

To find the volume of a pyramid we need to know the base area and height. The perpendicular distance from the apex to the center of the base of the polygon is known as the height of the pyramid.

Volume of a Pyramid Formula

The volume of the pyramid with the area of the base “A” and the height “h” is given by

Volume $V= \frac{1}{3} Ah$ 

Volume Formulas of Different Types of Pyramids

Let’s see the volume formula for different pyramids. 

1. Triangular pyramid

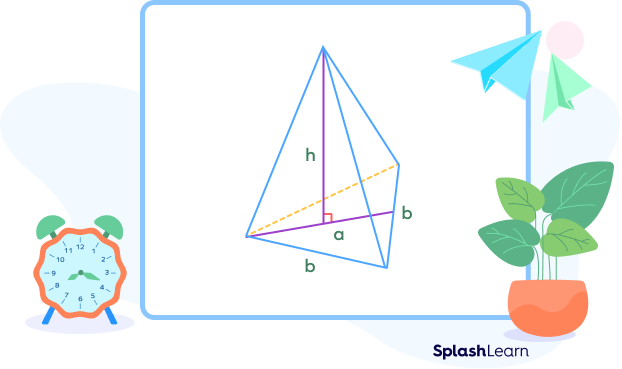
$V = \frac{1}{3} Ah$ 

where, the base is a triangle and the base area is given by

$\text{A} = \frac{1}{2} \times base \times height$

2. Square Pyramid

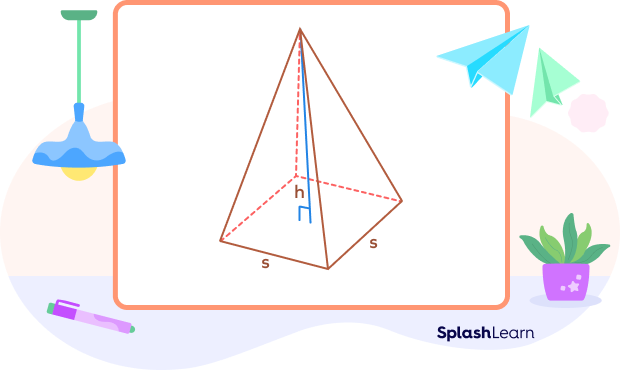
Let’s learn the formula for the volume of a square pyramid. To find the volume of a pyramid with square base, we use the following formula: 

$V = \frac{1}{3} Ah$ 

where, 

$A = side^{2} = s^{2}$

3. Rectangular Pyramid

$V = \frac{1}{3} Ah$ 

Where, 

$A = length \times width$

4. Pentagonal Pyramid

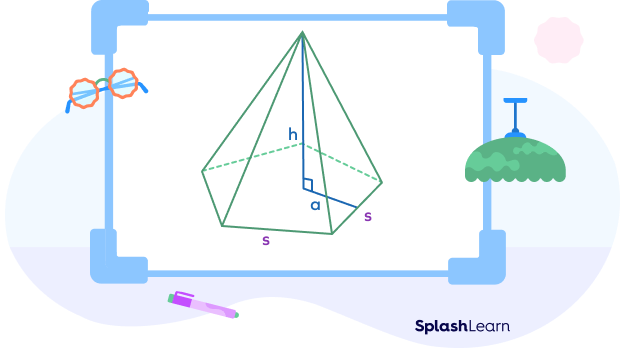
$V = \frac{1}{3} Ah$ 

Where, 

$A = base area = \frac{5}{2} \times a \times s$

5. Hexagonal Pyramid

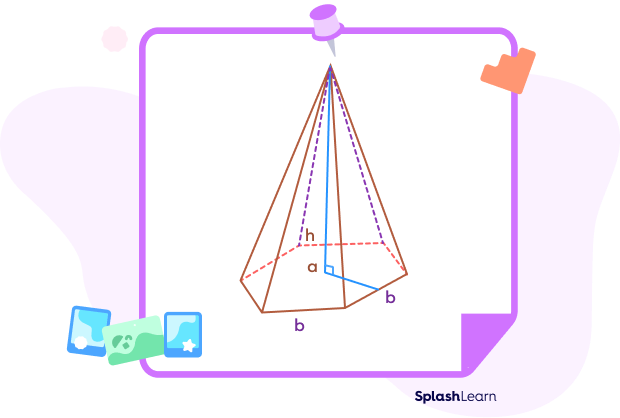
$V = \frac{1}{3} Ah$ 

where, $A= \frac{3\sqrt{3s2}}{2}$

OR

$V = a \times s \times h$

where, 

a $=$ apothem length

s $=$ length of a side of the base

h $=$ height of the prism.

How to Find the Volume of a Pyramid

Step 1: Find the area of the base A. If the base is a rectangle, then we find the area as $(\text{length} \times \text{width})$. If it is a square, then we find the area by the formula $(\text{side}^{2})$. 

Step 2: Note down the height h, the distance from the center of the base to the apex. 

Step 3: Now we put the values in the formula. The formula shall be discussed later in the article.

Example: Consider a square pyramid with given dimensions.

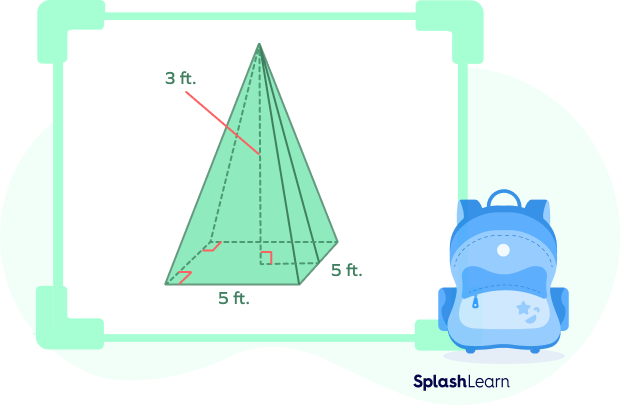
Since the base is a square, we have 

Base area $= side^{2} = 5^{2} = 25$ sq. ft.

Height $= h = 3$ ft

Volume $= V = \frac{1}{3} Ah = \frac{1}{3} \times 25 \times 3 = \frac{75}{3} = 25$ cubic ft.

Fun Facts!

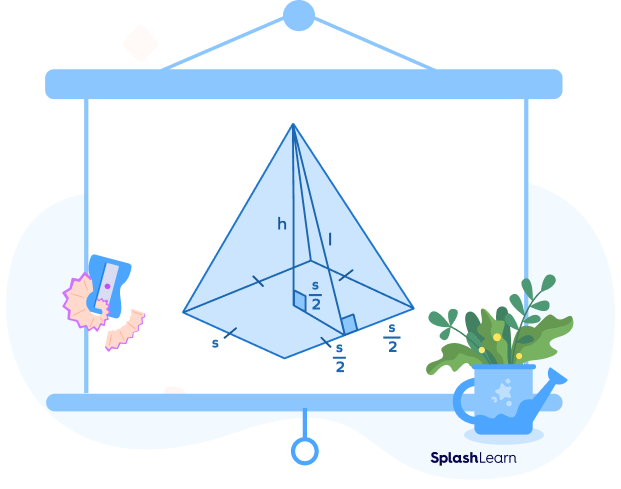
• Pyramids are the 3D shapes that hold significance in Egyptian history.

• The triangle formed by the height $(h)$, half the side $(\frac{s}{2})$ and the slant height (l) is the right triangle.

Conclusion

In this article, we learned about the volume of a pyramid, and formulas for different types of pyramids. Let’s solve some examples and practice problems for better understanding. 

Solved Examples

1. A square pyramid has a base dimension $20 \text{ft} \times 20 \text{ft}$ and its height is around 30 ft. Calculate its volume.

Solution:

The given pyramid is a square pyramid. Its base area is:

$\text{A} = 20 \times 20 = 400$ square feet

The height of the pyramid is, $h = 30$ ft

Using the volume of pyramid formula,

$V = \frac{1}{3} \times 400 \times 30$ 

$V = 4000$ cubic feet

The volume of the given square pyramid is 4000 cubic feet.

2. A triangular pyramid has a base area of 200 sq. ft and height 6 ft. Find its volume.

Solution:

Base area $= \text{A} = 200$ sq. ft

Height $= \text{h} = 6$ ft

Volume of given triangular pyramid $= \frac{1}{3} \times 200 \times 6$

    $\text{V} = 400$ cubic feet

3. Kelly built a tent that is of the shape of a rectangular pyramid. The base of the tent is a rectangle with dimensions 7 units $\times$ 10 units and the height is 9 units. What is the volume of the tent?

Solution:

The base area of the tent is the area of the rectangle.

Area of the base $=$ area of rectangle $= 7 \times 10 = 70$ square units.

The height of the tent is $\text{h} = 9$ units

The volume of the tent using the volume of pyramid formula is,

$V = \frac{1}{3} Ah$ 

$V = \frac{1}{3} \times 70 \times 9$

$V = 210$ cubic units

The volume of the tent $= 210$ cubic units

4. A pyramid has a square base with side 8 ft and a height of 12 ft. Find its volume.

Solution:

The given pyramid is a square pyramid. Its base area is,

$A = 8 \times 8 = 64$ square feet.

The height of the pyramid is, $\text{h} = 12$ ft

Using the volume of pyramid formula,

Volume of pyramid, 

$V = \frac{1}{3} Ah$ 

$V = \frac{1}{3} \times  64 \times 12$ cubic ft

$V = 256$ cubic feet.

The volume of the given pyramid is 256 cubic feet.

5. For the triangular pyramid, the area of the base is $49 \text{cm}^{2}$. Find its volume if the height of the pyramid is 6 cm.

Solution:

Given the area of the base of pyramid $= 49 \text{cm}^{3}$

Volume of Pyramid,

$V = \frac{1}{3} Ah$ 

$V = \frac{1}{3} \times 49 \times 6$

$V = 98$ $cm^{3}$

The volume of the given pyramid is $98$ $cm^{3}$.

Practice Problems

Frequently Asked Questions